正多边形是如何画出来的?
前言:以基础尺柜作图可以作出何种正多边形?
一,尺规作图的简介
尺规作图有多种功能 :
1.作相等的线段,角
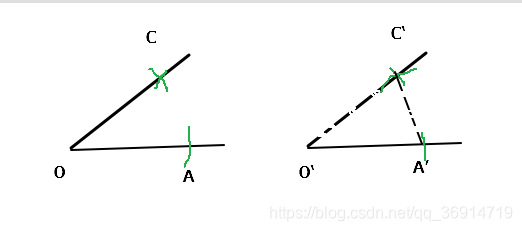
可在∠AOC上画一个圆 于是OA=OC 然后 再在线段O‘上取相等半径OA画圆
再截取AC的长 在A‘处作圆 交圆O’于C’ 则△AOC ≌△A’O"C’ 这就作出了相等的角
2.加减乘除法的运算
加法:加法较为简单
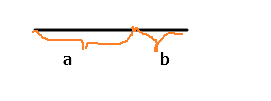
两个线段长度相加即可
减法同理 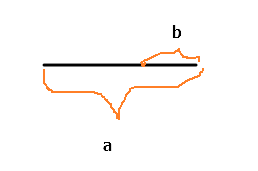
乘法:
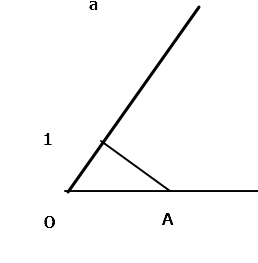
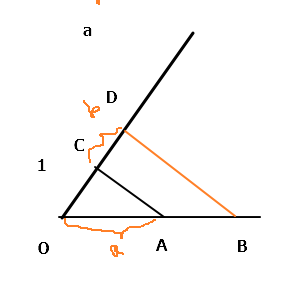
有一段线段OA 随便作一个角 然后在角上取单位线段1的长度
然后再在OC上取CD=b 作AC的平行线BD 交OA于点B
由相似三角形可知 OA/OC = AB/CD
则a*b = AB
除法同理 令AB =b 则 CD = a/b
3. 平方根的运算
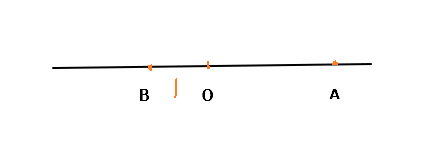
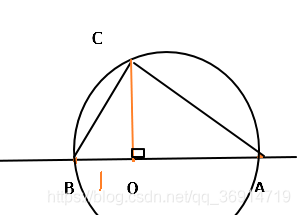
在OA上取OB为单位线段1
以AB为直径作圆 再作OC⊥AB 交圆于点C
则由射影定理(欧几里得定理)得 OC² = OA*OB
则OC = √OA
由此可见 基础尺规作图能表示加减乘除及开平方的数字
二 ,正多边形的计算方法
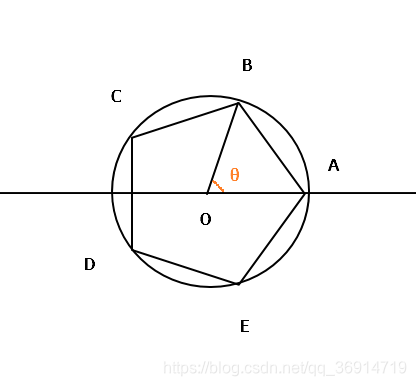
要作出正n边形 只要知道每一边的长度AB 其他边长都相同 也就是求出cosθ的大小
将圆心O看作复平面的中心 则ABCDE每一点的坐标分别为
A:cos0
B:cosθ
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!