h5 Canvas正多边形绘制

在之前文章中,我们使用线段进行绘制过矩形,使用arc,arcTo绘制过圆弧和圆形,但是Canvas还能够进行绘制其他图形,比如三角形、六边形、八边形等.这篇文章主要就是说明如何绘制多边形.

• html

canvas not supported

• JS

window.addEventListener('load', eventWindowLoaded, false);function eventWindowLoaded () {canvasApp(); // 包含整个Canvas应用程序
}
function canvasSupport(e) {return !!e.getContext;
}
function canvasApp() {let canvas = document.getElementById('canvas');Point = function (x, y) {this.x = x;this.y = y;};const colors = ['#f0f', '#eef', '#ff0', '#f0f', '#aaf', '#0f0', '#ccc', '#999', '#eee', '#ccc', '#606'];if (!canvasSupport(canvas)) {return;}let ctx = canvas.getContext('2d');canvas.width = window.innerWidth - 100;canvas.height = window.innerHeight - 50;function drawHorizontalAxis() {ctx.beginPath();ctx.moveTo(10, canvas.height / 2 + 0.5);ctx.lineTo(canvas.width - 10, canvas.height / 2);ctx.stroke();}function drawVerticalAxis() {ctx.beginPath();ctx.moveTo(canvas.width / 2, 10);ctx.lineTo(canvas.width / 2, canvas.height - 10);ctx.stroke();}function getPolygonPoints(centerX, centerY, radius, sides, startAngle) {const points = [];let angle = startAngle || 0;for (let i = 0; i < sides; ++i) {points.push(new Point(centerX + radius * Math.sin(angle),centerY - radius * Math.cos(angle)));angle += 2 * Math.PI / sides;}return points;}function createPolygonPath(centerX, centerY, radius, sides, startAngle) {const points = getPolygonPoints(centerX, centerY, radius, sides, startAngle);ctx.beginPath();ctx.moveTo(points[0].x, points[0].y);for (let i = 0; i < sides; ++i) {ctx.lineTo(points[i].x, points[i].y);}ctx.strokeStyle = colors[sides];ctx.closePath();}function drawRubberbandShape(currentSides) {createPolygonPath((canvas.width) / 2,(canvas.height) / 2,150, currentSides, Math.PI * 2);ctx.stroke();}function drawScreen() {ctx.lineWidth = 1;ctx.strokeStyle = '#b3c3de';ctx.font = '24px Arial';drawHorizontalAxis();drawVerticalAxis();let curSides = 3;setInterval(function() {drawRubberbandShape(curSides++);if (curSides > 10) {curSides = 3;ctx.clearRect(0, 0, canvas.width, canvas.height);drawHorizontalAxis();drawVerticalAxis();}}, 1200);}drawScreen();
}

效果如下:

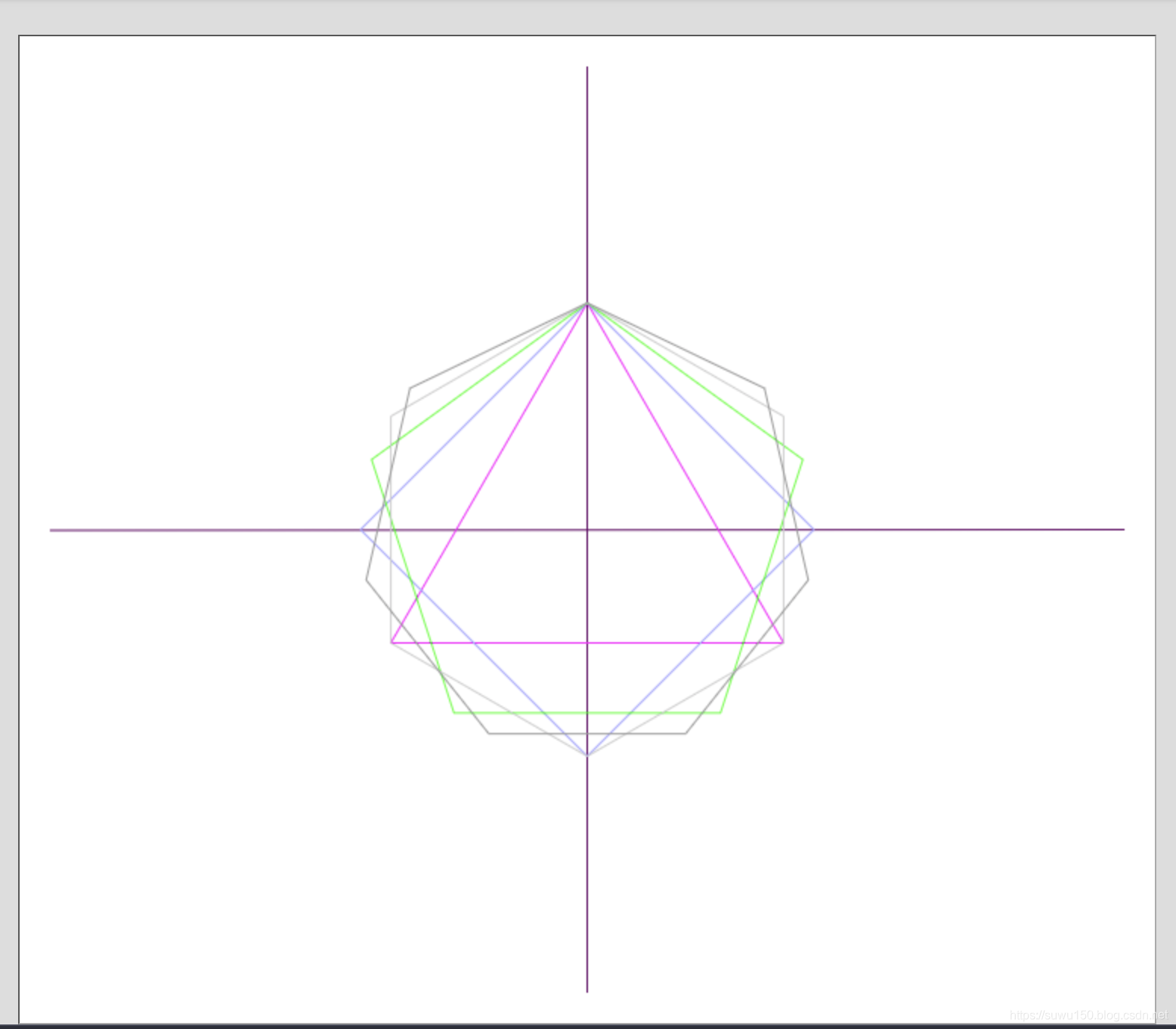
上述代码,我们进行绘制了一组根据时间进行变化的生成的多边形,通过方法drawHorizontalAxis绘制横向坐标轴,方法drawVerticalAxis绘制纵向坐标轴,通过方法getPolygonPoints进行计算获取多边形中所有的点,进行为后面连线时连接点作准备工作,通过createPolygonPath进行绘制具体的路径,其中使用循环的方式将points数组中坐标点进行连接,填充样式和描边,最后使用计时器进行控制图形的变化.
其实总的来说刚才绘图的模型就是下图所示,其中确定坐标点points数组的方式就是图中的(x,y)坐标.

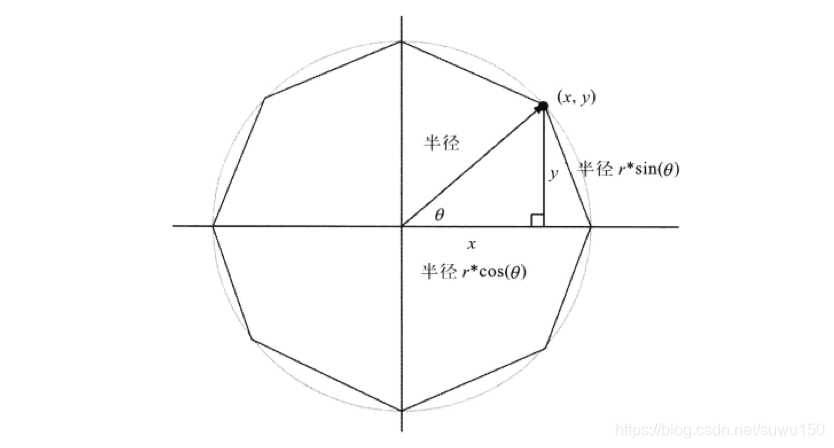
可以看到我们其实绘制的全都是正多边形.那我们就不得不说说正多边形.

正多边形

维基百科上是这样描述的：正多边形是所有角都相等、并且所有边都相等的简单多边形，简单多边形是指在任何位置都不与自身相交的多边形。

正多边形的特性

正n边形每个内角为(1 - 2 / n) * 180或者表示为(n - 2) * 180 / n角度。也可以用弧度表示为(n - 2) * π / n 或者(n - 2) / 2n。

正多边形的所有顶点都在同一个外接圆上，每个正多边形都有一个外接圆，这也称为圆内接正多边形。

上图描述了正多边形的相关属性：

正多边形的中心点正好是一个正多边形的外接圆的圆心
正多边形每条边的长度都相等，如上图中的x
正多边形的每个内角都相等，如上图中的β
正多边形的每个外角都相等，如上图中的α
正多边形的中心角都相等，如上图中的θ
正多边形的中心点距正多边形的内切圆的半行为r
正多边形的顶点数和边数相等，常用n表示
正多边形中心距正多边形的外接圆（或者正多边中心点距正多边形的顶点）就是正多边形外接圆半么，如上图中的R
正多边形中心点距和每条边的端点构成一个等腰三角形，如上图中的A1。这个三角形的两条边长度相等，刚好是正多边形外接圆半径R，而这个三角形的高，刚好是正多边形内切圆半径r

那么在Canvas中要使用CanvasRenderingContext2D对象自带的方法，比如moveTo()和lineTo()绘制多边形，我们就必须知道正多边形属性之间的关系。也就是这些属性之间的三角函数。言外之意，在Canvas中，我们使用moveTo()和lineTo()方法，再配合一些简单的三角函数，就可以绘制出任意边数的多边形。

下面我们在上面代码的基础上进行更加灵活的配置,希望通过进行选择进行绘制任意边数的正多边形.

参考链接
1.canvas绘制蜘蛛网图

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！