求三维空间下的两线交点，如果两线异面，返回它们公垂线的中点

Intersection_lines方法实现了如题的需求

#include 
#include
#include
#include
#include#define sign(x) ((x)>eps?1:((x)<-eps?(-1):(0)))const double eps = 1e-8, inf = 1e50;
using namespace std;class point3 {
public:double x, y, z;point3(double _x=0, double _y=0, double _z=0) {x = _x; y = _y; z = _z;}point3 operator-(const point3& ne) {return point3(x - ne.x, y - ne.y, z - ne.z);}point3 operator+(const point3& ne) {return point3(x + ne.x, y + ne.y, z + ne.z);}point3 operator*(const double t) {return point3(x * t, y * t, z * t);}friend ostream& operator<<(ostream& out, const point3& a);
};class plane3 {
public:point3 a, b, c;plane3(){}plane3(point3 _a, point3 _b, point3 _c) {a = _a;b = _b;c = _c;}};class line3 {
public:point3 a, b;line3() {}line3(point3 _a, point3 _b) {a = _a;b = _b;}
};//叉乘，返回向量
point3 xmult(point3 a, point3 b) {return point3(a.y * b.z - a.z * b.y, a.z * b.x - a.x * b.z, a.x * b.y - a.y * b.x);
}
//点乘
double dmult(point3 a, point3 b) {return a.x * b.x + a.y * b.y + a.z * b.z;
}
point3 Vec(point3 a, point3 b) {return point3(a.x - b.x, a.y - b.y, a.z - b.z);
}
double length(point3 v) {return sqrt(v.x * v.x + v.y * v.y + v.z * v.z);
}//判断直线平行
bool parallel(line3 u, line3 v) {return sign(length(xmult(u.b - u.a, v.b - v.a))) == 0;
}//平面法向量
point3 pvec(plane3 s) {return xmult(s.b - s.a, s.c - s.a);
}//线线求交
point3 line_interseciton(line3 u, line3 v) {point3 ret = u.a, v1 = xmult(u.a - v.a, v.b - v.a), v2 = xmult(u.b - u.a, v.b - v.a);double t = length(v1) / length(v2) * (dmult(v1, v2) > 0 ? -1 : 1);return ret + ((u.b - u.a) * t);
}
//线面求交
point3 line_plane_intersection(line3 u, plane3 s) {point3 ret = pvec(s), der = u.b - u.a;double t = dmult(ret, s.a - u.a) / dmult(ret, u.b - u.a);return u.a + der * t;
}
//判断两直线的位置关系
int line_to_line(line3 u, line3 v) {plane3 s1(u.a, u.b, v.a), s2(u.a, u.b, v.b);if (sign(length(xmult(pvec(s1), pvec(s2)))))return -1;//异面else if (parallel(u, v))return 0;//平行elsereturn 1;//相交
}//直线到直线的距离 w是垂直向量，根据w算出标量
double Common_Vertical_Line(line3 u, line3 v, point3 &w) {w = xmult(u.a - u.b, v.a - v.b);return fabs(dmult(u.a - v.a, w) / length(w));
}
//求三维下的两线交点
bool Intersection_lines(line3 L1,line3 L2,point3& insc) {int relationship = line_to_line(L1, L2);switch (relationship) {case 1:                     //相交insc = line_interseciton(L1, L2);return true;case 0:                     //平行return false;case -1: {        //异面point3 v;double closestDist = Common_Vertical_Line(L1, L2, v); //两直线的最近距离plane3 p1(L1.a, L1.b, L1.a + v), p2(L2.a, L2.b, L2.a + v);point3 line1_ans = line_plane_intersection(L1, p2); //交点point3 line2_ans = line_plane_intersection(L2, p1); //交点insc.x= (line1_ans.x + line2_ans.x) / 2;insc.y = (line1_ans.y + line2_ans.y) / 2;insc.z = (line1_ans.z + line2_ans.z) / 2;return true;}default:return false;}
}//输入四个点，求交点法线的起点终点bool get_joint_track_pt4(line3 L1,line3 L2,double dis,point3 &beg,point3 &end) {if (Intersection_lines(L1, L2,beg) == false ||dis == 0) {return false;}point3 p1 = length(L1.a) > length(L1.b) ? L1.a : L1.b;point3 p2 = length(L2.a) > length(L2.b) ? L2.a : L2.b;plane3 plane(p1, p2,beg);//三点构造一个面point3 vert = pvec(plane);if (vert.z * dis < 0) {plane3 plane_reverse(p2, p1, beg);vert = pvec(plane_reverse);}cout << "vert = " << vert << endl;double ratio = abs(length(vert) / dis);end.x = beg.x + vert.x / ratio;end.y = beg.y + vert.y / ratio;end.z = beg.z + vert.z / ratio;return true;
}//入口函数是get_joint_track_pt4传入两条线L1,L2
//dis是焊接距离
//beg是焊接起点，end是焊接终点
int main()
{//测试用例point3 pt1(-1, 1,1), pt2(2, 1, 1), pt3(0, 2, 1), pt4(0, 5, 1), beg, end;double dis = -15;line3 L1(pt1, pt2);line3 L2(pt4, pt3);get_joint_track_pt4(L1, L2, dis, beg, end);cout << beg << endl;cout << end << endl;system("pause");return 0;
}ostream& operator<<(ostream& out, const point3& a)
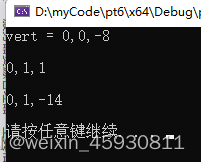
{out << a.x << "," << a.y << "," << a.z << endl;return out;
}

运行结果：（不受点的传入顺序影响）

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！