【信号与系统】（十二）傅里叶变换与频域分析——信号分解为正交函数

文章目录

• 信号分解为正交函数
• • 1 矢量的正交分解
  • 2 信号的正交分解
  • 3 帕斯瓦尔定理

信号分解为正交函数

1 矢量的正交分解

（1）矢量正交
复习：两矢量 V 1 V_1 V1​与 V 2 V_2 V2​正交，夹角为90°

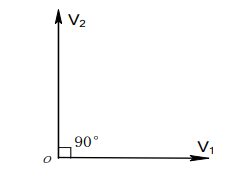
两正交矢量的内积为零

（2）正交矢量集
由两两正交的矢量组成的矢量集合。

（3）非正交矢量的近似表示及误差

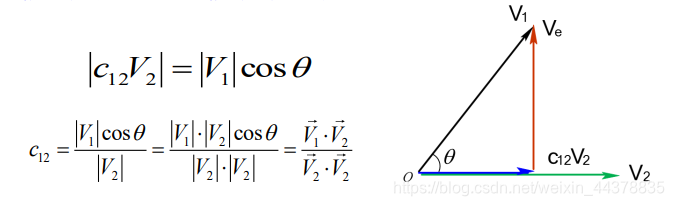
用与 V 2 V_2 V2​成比例的矢量 c 12 V 2 c_{12}V_2 c12​V2​近似地表示 V 1 V_1 V1​，则误差矢量

显然，当两矢量 V 1 V_1 V1​与 V 2 V_2 V2​正交时， c 12 = 0 c_{12}=0 c12​=0，即 V 1 ⋅ V 2 = 0 V_1·V_2=0 V1​⋅V2​=0。

（4）矢量正交分解：任意$N$维矢量可由N维正交坐标系表示。

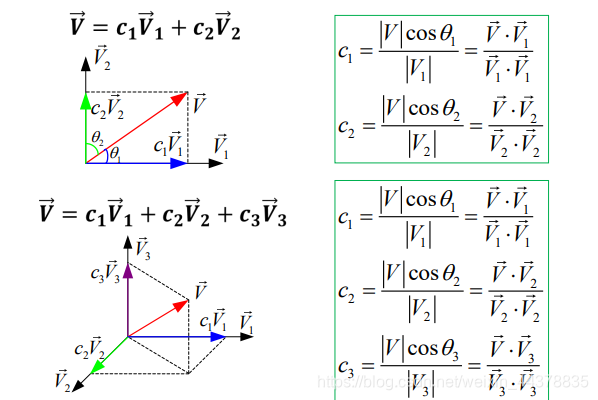
推广到$n$维空间：$n$维空间的任一矢量$V$，可以精确地表示为$n$个正交矢量的线性组合， 即

式中， V i ⋅ V j = 0 ( i ≠ j ) V_i·V_j=0 (i≠j) Vi​⋅Vj​=0(i​=j)，第 $r$ 个分量的系数

思路：将矢量空间正交分解的概念可推广到信号空间：在信号空间找到若干个相互正交的信号作为基本信号，使得信号空间中任意信号均可表示成它们的线性组合。

2 信号的正交分解

（1）信号正交

注意是在区间内，超出区间就不一定了。
（2）正交函数集

（3）完备正交函数集

没有其他非零$\phi (t)$与 φ i \varphi_i φi​正交，即把全部找到。

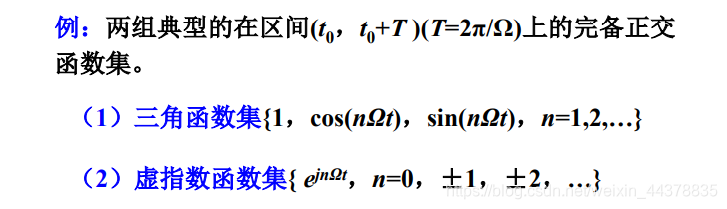
（4）信号的正交分解

和的平方$\ge$平方和

$\ast$：共轭

备注：这里的 φ i ( t ) \varphi_i(t) φi​(t)就是你要找的正交函数。

3 帕斯瓦尔定理

帕斯瓦尔方程：

物理意义：在区间 ( t 1 , t 2 ) (t_1,t_2) (t1​,t2​)， 信号$f(t)$所含有的能量``恒等于此信号在完备正交函数集中各正交分量能量之和，即能量守恒定理, 也称帕斯瓦尔定理。

数学本质：矢量空间信号正交变换的范数不变性。

《工程信号与系统》作者：郭宝龙等
中国大学MOOC：信号与系统 ，西安电子科技大学，郭宝龙，朱娟娟

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！