完备正交函数集有如下两个定理
(1)任何一个信号f(t)都可以在区间(t1,t2)内精确地表示为这个完备正交函数集中各函数的线性组合,即:
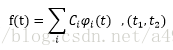
其中Ci为加权系数,Ci为:
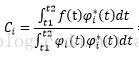
上式称为正交展开式,有时也称为广义傅里叶级数,Ci称为傅里叶系数。
注:若基函数满足单位正交性且为实数,即(如,三角函数集满足此条件),那么可写作:
![]()
(2)在(1)的条件下,根据此时均方误差为0,可得:
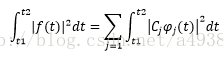
这就是帕塞瓦尔(Parseval)方程(等式)。它表明,在区间(t1,t2),信号f(t)的能量恒等于f(t)在完备正交函数集中分解的各正交分量能量之和。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!