1、最大子列和问题（包含4种算法）

1、最大子列和问题

题目

在一个列表中，有许许多多的子列，我们的目的，就是求最大子列和是多少。

例如{-2，11，-4，13，-5，-2}，最大子列是{11，-4，13}，和为20。

主函数

#include
#define N 100000
int findMax(int num[],int n);
int main()
{int i,n,maxSum;printf("输入该列表的元素个数");scanf("%d", &n);int num[N];printf("输入列表中的元素");for (i = 0; i < n; i++)scanf("%d", &num[i]);maxSum = findMax(num, n);printf("最大子列和是%d", maxSum);
}

​ 最优先的想到的解法就是穷举法。把一个列表中所有子列的和求出来，就可以得出结果。用i循环规定子列左边，用j循环规定子列右边，再用一个k循环把[i:j]中所有值加起来，就完成了穷举法。

第一次求和

第二次求和

。。。

。。。

。。。

最后一次求和

代码如下：

穷举法：

int findMax(int num[], int n)
{int i, j, k, maxSum = 0;int sum;for (i = 0; i < n; i++){for (j = i; j < n; j++){sum = 0;for (k = i; k <= j; k++)sum += num[k];if (sum > maxSum)maxSum = sum;}}return maxSum;
}

​ 其实穷举是能优化的，每次循环无非就是加上下一个数，所以我们直接去了一个循环，改为沿用上一次计算出的结果，这样就少了一次循环，时间复杂度就减少一个幂。

穷举法的改进：（运行时间显著减少）

int findMax(int num[], int n)
{int i, j, maxSum = 0;int sum;for (i = 0; i < n; i++){sum = 0;for (j = i; j < n; j++){sum += num[j];if (sum > maxSum)maxSum = sum;}}return maxSum;
}

​ 简而言之，我们所使用的方法可以解决这个问题，但是，在处理大规模数据的时候，运行速度将非常慢，我们使用更好的算法，优化它。

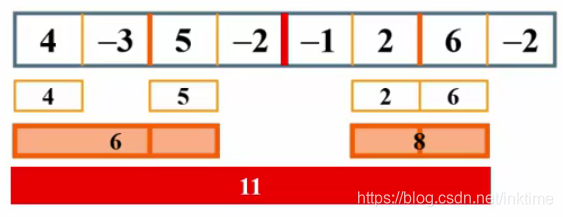
​ 分而治之，简单的说，就是把一个列表从中间分开，求左边，右边，和跨越中间的最大值，最后进行比较。跨越中间的简单，穷举法分别求从中间开始的左边和右边最大值，然后加起来。求两边的最大值则又回到了这个题目的起点，这不就是递归吗？我们把左边的列表一次一次的拆分，直到只剩下一个，再一次又一次的找出最大的值，最后一层层的比较，最终得出结果。

分而治之法：

//返回3个数中最大的一个值
int max3(int A, int B, int C)
{if (A > B && A > C)return A;elseif (B > C)return B;elsereturn C;
}//分而治之的方法
int divideWay(int num[], int left,int right)
{int maxLeft, maxRight;//存放左右最大值int maxMidLeft, maxMidRight, maxMid;//存放跨中线左边和右边的最大值int i, mid = 0;int max1 = 0, max2 = 0;if (right == left)//递归在分到只有一个元素终止if (num[left] > 0)return num[left];elsereturn 0;mid = (left + right) / 2;//分开maxLeft = divideWay(num, left, mid);//递归求左边最大值maxRight = divideWay(num, mid+1, right);//递归求右边最大值//以下部分求跨中线的最大值maxMidLeft = 0, maxMidRight = 0;for (i = mid; i >= left; i--){max1 += num[i];if (max1 > maxMidLeft)maxMidLeft = max1;}for (i = mid+1; i <= right; i++){max2 += num[i];if (max2 > maxMidRight)maxMidRight = max2;}maxMid = maxMidLeft + maxMidRight;//找到最大值return max3(maxLeft, maxRight, maxMid);
}//返回函数接口
int findMax(int num[], int n)
{return divideWay(num, 0, n - 1);
}

​ 这么来看，我们已经得到一个相当不错的算法。但递归也有缺陷，比如占用内存大，程序复杂难懂。因此，有人提出了第四个算法，在线处理算法。

​ 这个算法只用一次循环，对于效率的提高不止一点两点了。

​ 我的理解是，从头开始累加，每加一次进行一次判断，如果当前和sum < 0，那就把它舍去。因为无论下一个数是多少，负数sum加上它，它一定会更小，因此舍弃，从零开始加，这样便能找到最大的一个数。

​ -6舍去，sum变为0，这就意味着从第二位开始加，加到第三位为7，加到第四位为6，因此输出7.

在线处理：

//在线处理算法
int findMax(int num[], int n)
{int i,maxsum = 0,sum = 0;for (i = 0; i < n; i++){sum += num[i];if (sum < 0)sum = 0;if (sum > maxsum)maxsum = sum;}return maxsum;
}

​ 这是第一次接触算法题，之前的题目，无论算法多么垃圾，但数据小，运行速度就基本没有区别。今天终于见识到，一个好的算法对一个程序的提升有多么重要。

​ 今天看知乎，有人问圆周率够用就行，为什么算到小数点后30万亿位？我想我找到了答案，可能，这就是千百年来，人们一直执着于改进算法的原因吧。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！