数据结构 最大子列和问题

题目：给定n个整数的序列{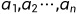},求函数f(i,j)=max{0,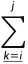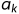}的最大值。

首先，要理解什么是最大的子列和？

在这里，“子列”被定义为原始序列中连续的一段数字。

我们的任务是：找到具有最大和的一段连续子列，并且返回它的和。（注：如果这个最大和是负数，那我们规定最终取0为最终答案）

举一个例子：例如给定序列{-2,11,-4,13,-5,-2},其最大子列为{11,-4,13},和为20。

回到题目，解决这个问题至少有4种不同的算法

方法一：直接法。穷举所有子列和，从中找出最大值。

方法一的时间复杂度由3层for循环决定的，即O()。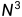

int MaxSubseqSum1(int List[],int N)
{    int i,j,k;int ThisSum,MaxSum=0;for(i=0;i=MaxSum)/*如果刚得到的这个子列和更大*/MaxSum=ThisSum;  /*则更新结果*/}    /*j循环结束*/        }    /*i循环结束*/return Maxsum;    /*返回最大子列和*/
}

方法二：部分存储中间值的穷举。

算法复杂度：该程序的时间复杂度是由2层嵌套的for循环决定的，所以该算法复杂度为O()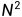

int MaxSubseqSum2(int List[],int N)
{    int i,j;int ThisSum,MaxSum=0;for(i=0;iMaxSum)    /* 如果刚得到的这个子列和更大 */MaxSum=ThisSum;    /*则更新结果*/}    /*j循环结果*/}    /*i循环结果*/return MaxSum;
}

方法三：分而治之（简称“分治法”）。

基本思路：将原问题拆分成若干小型问题，分别解决后再将结果合而治之，用递归实现非常方便。

int Max3(int A,int B, int C)
{    /*返回3个整数中的最大值*/return A>B?A>C?A:C:B>C?B:C;
}int DivideAndConquer(int List[],int left,int right)
{    /*分治法求List[left]到List[right]的最大子列和*/int MaxLeftSum,MaxRightSum;    /*存放左右子问题的解*/int MaxLeftBorderSum,MaxRightBorderSum;    /*存放跨分界线的结果*/int LeftBorderSum,RightBorderSum;int center,i;if(left == right){    /*递归的终止条件，子列只有1个数字 */if(List[left]>0)    return List[left];else return 0;}/*下面是“分”的过程*/center=(left+right)/2;    /*找到中分点*//*递归求得两边子列的最大和*/MaxLeftSum=DivideAndConquer(List,left,center);MaxRightSum=DivideAndConquer(List,center+1,right);/*下面求夸分界线的最大子列和*/MaxLeftBorderSum=0; LeftBorderSum=0for (i=center;i>=left;i--)    /*从中线向右扫描*/{RightBorderSum+=List[i];if(RightBorderSum>MaxRightBorderSum)MaxRightBorderSum=RightBorderSum;}    /*右边扫描结束*//*下面是返回“治”的结果*/return Max3(MaxLeftSum,MaxRightSum,MaxLeftBorderSum+MaxRightBorderSum);
}int MaxSubseqSum3(int List[],int N)
{    /*保持与前2种算法相同的函数接口*/return DivideAndConquer(List,0,N-1);
}

时间复杂度：O(N log N )。

方法四：在线处理

含义：指每输入一个数据就进行及时处理，得到结果是对于当前已经读入的所有数据都成立的解，即在任何一个地方中止输入，算法都能给出当前的解。

int MaxSubseqSum4(int List[],int N)
{int i;int ThisSum,MaxSum;ThisSum=MaxSum=0;for(i=0;iMaxSum)MaxSum=ThisSum; /*发现更大和则更新当前结果*/else if(ThisSum<0)  /*如果当前子列和为负*/ThisSum=0;  /*则不可能使后面的部分和增大，抛弃之*/}return MaxSum;
}

算法复杂度：O(N)

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！