使用一阶微分对图像锐化
Using First-Order Derivatives for (Nonlinear)Image Sharpening ----The Gradient
对于函数ƒ(x,y), ƒ在坐标(x,y)处的梯度定义为二维列向量

(1)
它指出了在位置(x,y)处ƒ的最大变化率的方向。
向量▽ƒ的幅度值(长度)表示为M(x,y),即

(2)
它是梯度向量方向变化率在(x,y)的值。当x,y允许在ƒ中的所有像素位置变化时,M(x,y)是与原图像大小相同的图像。通常该图像称为梯度图像(简称为梯度)。
在某些实现中,用绝对值来近似平方和平方根操作更合适计算

(3)
该表达式仍保留了灰度的相对变化,但是失去了各向同性特征。
gx,gy近似表示为
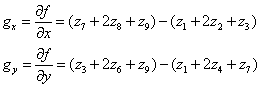
(4)
这两个公式可以用以下两个模板实现,(a)中的模板实现的3x3图像区域的第三行和第一行的差近似x方向的微分,(b)模板中的第三列和第一列的差近似了y方向的微分。
| -1 | -2 | -1 |
| 0 | 0 | 0 |
| 1 | 2 | 1 |
(a)
| -1 | 0 | 1 |
| -2 | 0 | 2 |
| -1 | 0 | 1 |
(b)
附上我的MATLAB实现代码
%%%%%%%梯度锐化图像(sobel算子)%%%%%%%Mask = 3; %滤波器模板大小(3x3)ImageDataTemp = imread('lena.jpg'); %读取工程目录下的图片
ImageDataGray = rgb2gray(ImageDataTemp); %转换为灰度图像
ImageResult = size(ImageDataGray); %存储处理后的图像
clear ImageDataTemp; %清除过程变量
Temp = padarray(ImageDataGray, [(Mask-1)/2 (Mask-1)/2]); %扩展图像,防止算子模板覆盖在图像外
[j,k] = size(ImageDataGray);SobelOperatorsX = [-1 -2 -1 0 0 01 2 1];
SobelOperatorsY = [-1 0 1-2 0 2-1 0 1];
Part = zeros(3, 3, 'double');
for x = 2:j+1for y = 2:k+1Part = double(Temp(x - 1 : x + 1, y - 1 : y + 1));ImageResult(x - 1, y - 1) = abs(sum(sum(times(Part,SobelOperatorsX)))) + abs(sum(sum(times(Part,SobelOperatorsY))));end
end
figure(1),imshow(ImageResult, []);
figure(2),imshow(ImageDataGray, []); 效果图:

转载于:https://www.cnblogs.com/tcysky/p/5906769.html
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!