MATLAB .一元函数的图形
1.命令plot的基本形式
x=a:t:b;
y=f(x);
plot(x,y,'s')
其中其中f(x)要代入具体的函数,也可以将前面已经定义的函数f(x)代入。a和b分别表示自变量x的最小值和最大值,即说明作图时自变量的范围,必须输入具体的数值。1表示取点间隔(增量),因此这里的x,y是向量。s是可选参数,用来指定绘制曲线的线型、颜色,数据点形状等。线型、颜色和数据点可以同时选用。
例1.作出y=x.^2函数在区间-1
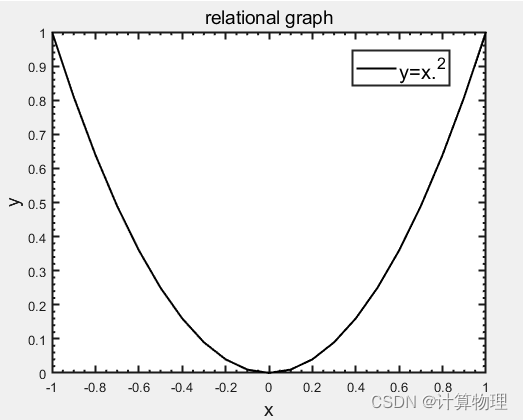
例1.代码
clc;clear;
a=-1;
b=1;
t=0.1;
x=a:t:b;
y=x.^2;
plot(x,y,'k','LineWidth',1.5)
%设置边框宽度坐标轴美化
legend({'y=x.^2'},'FontSize',15);
xlabel({'x'},'FontSize',14);
ylabel({'y'},'FontSize',14);
title({'relational graph'},'FontSize',14);
set(gca,'linewidth',1.5);
set(gca,'XGrid', 'off', 'YGrid', 'off', ... 'TickDir', 'in', 'TickLength', [.015 .015], ... 'XMinorTick', 'on', 'YMinorTick', 'on', ... 'XColor', [.1 .1 .1], 'YColor',[.1 .1 .1]);
2.隐函数作图命令ezplot
ezplot(f(x,y),[xmin,xmax,ymin,ymax])
该命令执行后绘制出由方程f(x,y)=0所确定的隐函数在区域:
xmin<=x<=xmax,ymin<=y<=ymax%内的图形。
命令中的第二项[xmin,xmax,ymin,ymax]给出了变量x与y的范围。
例2,方程(x^2+y^2)^2=x^2-y^2确定了y是x的隐函数,作出它的图形。
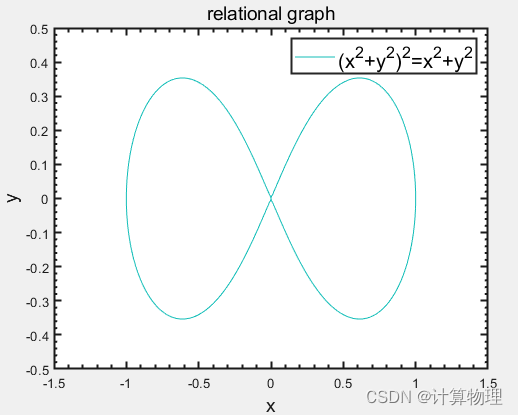
例2.代码
x=-1.5:1.5;y=-0.5:0.5;
ezplot('(x.^2+y.^2).^2-x^2+y^2',...[min(x),max(x),min(y),max(y)]);
%设置边框宽度坐标轴美化
legend({'(x^2+y^2)^2=x^2+y^2'},'FontSize',15);
xlabel({'x'},'FontSize',14);
ylabel({'y'},'FontSize',14);
title({'relational graph'},'FontSize',14);
set(gca,'linewidth',1.5);
set(gca,'XGrid', 'off', 'YGrid', 'off', ... 'TickDir', 'in', 'TickLength', [.015 .015], ... 'XMinorTick', 'on', 'YMinorTick', 'on', ... 'XColor', [.1 .1 .1], 'YColor',[.1 .1 .1]);
3.极坐标方程作图
如果想利用曲线的极坐标方程作图,可使用ploar命令。其基本形式是:
polar(theta,rho);
例3.曲线的极坐标方程为d=9*cos(9*b),要作出它的图形
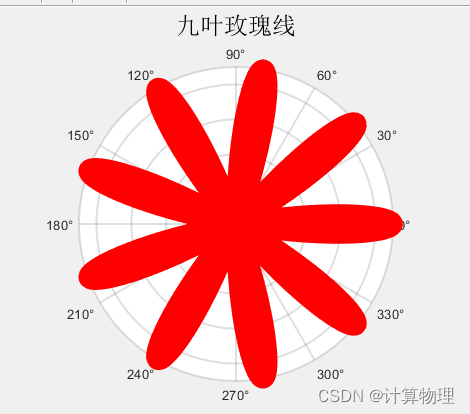
例3.代码
clc;clear;
theta=0:0.01:2*pi;
rho=9*cos(9*theta);
polarplot(theta,rho,'r','LineWidth',15);
%便得到了一条九叶玫瑰线
title({'九叶玫瑰线'},'FontSize',18);
%设置边框宽度坐标轴美化
set(gca,'linewidth',1.5);
set(gca,'XGrid', 'off', 'YGrid', 'off', ... 'TickDir', 'in', 'TickLength', [.015 .015], ... 'XMinorTick', 'on', 'YMinorTick', 'on', ... 'XColor', [.1 .1 .1], 'YColor',[.1 .1 .1]);
4.分段函数作图
分段函数的定义用到条件语句,而条件语句根据具体条件分支的方式不同,可有多种不同形式的if语句块。这里仅给出较为简单的三种条件语句块:
(1)if<条件表达式> 语句体 end
(2)if<条件表达式> 语句体1 else 语句体2 end
(3)if<条件表达式1> 语句体1 elseif<条件表达式2> 语句体2 else 语句体3 end
例4.作出y=10*sin(10*x)+10*cos(11*x)函数在区间-4
作出y=exp(x)函数在区间0
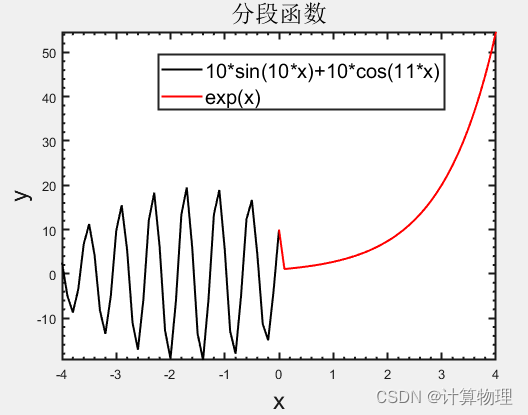
例4.代码
clc;clear;
y=[];x0=-4:0.1:4;
for x=-4:0.1:4;if x<=0;y=[y,10*sin(10*x)+10*cos(11*x)];endif x>0;y=[[y,exp(x)]];end
end
plot(x0(1:41),y(1:41),'k','LineWidth',1.5); hold on
plot(x0(41:81),y(41:81),'r','LineWidth',1.5); hold on
axis([min(x0) max(x0) min(y) max(y)]);
set(gca,'linewidth',1.5);
xlabel({'x'},'FontSize',18);
ylabel({'y'},'FontSize',18);
legend({'10*sin(10*x)+10*cos(11*x)','exp(x)'},'FontSize',15);
title({'分段函数'},'FontSize',18);
%设置边框宽度坐标轴美化
set(gca,'XGrid', 'off', 'YGrid', 'off', ... 'TickDir', 'in', 'TickLength', [.015 .015], ... 'XMinorTick', 'on', 'YMinorTick', 'on', ... 'XColor', [.1 .1 .1], 'YColor',[.1 .1 .1]);
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!

例1.代码
clc;clear;
a=-1;
b=1;
t=0.1;
x=a:t:b;
y=x.^2;
plot(x,y,'k','LineWidth',1.5)
%设置边框宽度坐标轴美化
legend({'y=x.^2'},'FontSize',15);
xlabel({'x'},'FontSize',14);
ylabel({'y'},'FontSize',14);
title({'relational graph'},'FontSize',14);
set(gca,'linewidth',1.5);
set(gca,'XGrid', 'off', 'YGrid', 'off', ... 'TickDir', 'in', 'TickLength', [.015 .015], ... 'XMinorTick', 'on', 'YMinorTick', 'on', ... 'XColor', [.1 .1 .1], 'YColor',[.1 .1 .1]);2.隐函数作图命令ezplot
ezplot(f(x,y),[xmin,xmax,ymin,ymax])
该命令执行后绘制出由方程f(x,y)=0所确定的隐函数在区域:
xmin<=x<=xmax,ymin<=y<=ymax%内的图形。
命令中的第二项[xmin,xmax,ymin,ymax]给出了变量x与y的范围。
例2,方程(x^2+y^2)^2=x^2-y^2确定了y是x的隐函数,作出它的图形。

例2.代码
x=-1.5:1.5;y=-0.5:0.5;
ezplot('(x.^2+y.^2).^2-x^2+y^2',...[min(x),max(x),min(y),max(y)]);
%设置边框宽度坐标轴美化
legend({'(x^2+y^2)^2=x^2+y^2'},'FontSize',15);
xlabel({'x'},'FontSize',14);
ylabel({'y'},'FontSize',14);
title({'relational graph'},'FontSize',14);
set(gca,'linewidth',1.5);
set(gca,'XGrid', 'off', 'YGrid', 'off', ... 'TickDir', 'in', 'TickLength', [.015 .015], ... 'XMinorTick', 'on', 'YMinorTick', 'on', ... 'XColor', [.1 .1 .1], 'YColor',[.1 .1 .1]);3.极坐标方程作图
如果想利用曲线的极坐标方程作图,可使用ploar命令。其基本形式是:
polar(theta,rho);
例3.曲线的极坐标方程为d=9*cos(9*b),要作出它的图形

例3.代码
clc;clear;
theta=0:0.01:2*pi;
rho=9*cos(9*theta);
polarplot(theta,rho,'r','LineWidth',15);
%便得到了一条九叶玫瑰线
title({'九叶玫瑰线'},'FontSize',18);
%设置边框宽度坐标轴美化
set(gca,'linewidth',1.5);
set(gca,'XGrid', 'off', 'YGrid', 'off', ... 'TickDir', 'in', 'TickLength', [.015 .015], ... 'XMinorTick', 'on', 'YMinorTick', 'on', ... 'XColor', [.1 .1 .1], 'YColor',[.1 .1 .1]);4.分段函数作图
分段函数的定义用到条件语句,而条件语句根据具体条件分支的方式不同,可有多种不同形式的if语句块。这里仅给出较为简单的三种条件语句块:
(1)if<条件表达式> 语句体 end
(2)if<条件表达式> 语句体1 else 语句体2 end
(3)if<条件表达式1> 语句体1 elseif<条件表达式2> 语句体2 else 语句体3 end
例4.作出y=10*sin(10*x)+10*cos(11*x)函数在区间-4
作出y=exp(x)函数在区间0

例4.代码
clc;clear;
y=[];x0=-4:0.1:4;
for x=-4:0.1:4;if x<=0;y=[y,10*sin(10*x)+10*cos(11*x)];endif x>0;y=[[y,exp(x)]];end
end
plot(x0(1:41),y(1:41),'k','LineWidth',1.5); hold on
plot(x0(41:81),y(41:81),'r','LineWidth',1.5); hold on
axis([min(x0) max(x0) min(y) max(y)]);
set(gca,'linewidth',1.5);
xlabel({'x'},'FontSize',18);
ylabel({'y'},'FontSize',18);
legend({'10*sin(10*x)+10*cos(11*x)','exp(x)'},'FontSize',15);
title({'分段函数'},'FontSize',18);
%设置边框宽度坐标轴美化
set(gca,'XGrid', 'off', 'YGrid', 'off', ... 'TickDir', 'in', 'TickLength', [.015 .015], ... 'XMinorTick', 'on', 'YMinorTick', 'on', ... 'XColor', [.1 .1 .1], 'YColor',[.1 .1 .1]);
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!

例4.代码
clc;clear;
y=[];x0=-4:0.1:4;
for x=-4:0.1:4;if x<=0;y=[y,10*sin(10*x)+10*cos(11*x)];endif x>0;y=[[y,exp(x)]];end
end
plot(x0(1:41),y(1:41),'k','LineWidth',1.5); hold on
plot(x0(41:81),y(41:81),'r','LineWidth',1.5); hold on
axis([min(x0) max(x0) min(y) max(y)]);
set(gca,'linewidth',1.5);
xlabel({'x'},'FontSize',18);
ylabel({'y'},'FontSize',18);
legend({'10*sin(10*x)+10*cos(11*x)','exp(x)'},'FontSize',15);
title({'分段函数'},'FontSize',18);
%设置边框宽度坐标轴美化
set(gca,'XGrid', 'off', 'YGrid', 'off', ... 'TickDir', 'in', 'TickLength', [.015 .015], ... 'XMinorTick', 'on', 'YMinorTick', 'on', ... 'XColor', [.1 .1 .1], 'YColor',[.1 .1 .1]);本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!