通俗解释概率论与数理统计中随机变量X的含义

通俗解释概率论与数理统计中随机变量X的含义

正文

  为了解释清楚这一概念，以抛硬币实验为例，假设我们现在做了这样一个实验E：将一枚硬币抛掷三次，观察正面H、反面T出现的情况。我们可以列出所有可能的实验结果：{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}，其中HHH表示硬币三次都掷为正面，HHT表示第一二次为正面，第三次为反面，其他以此类推。
  现在让我们首先引入样本空间的概念：将实验E的所有可能结果组成的集合称为E的样本空间，记为S。样本空间的元素，称为样本点，记为e。这是书上的概念，现在来说点人话，所谓样本点，就是指实验E中的每个结果，如其中一个实验结果HHH，即硬币三次都被掷为正面，这就是一个样本点。所有样本点的集合就是样本空间，回到我们的例子中就是指{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}，即实验E中所有可能的结果放在一起就组成了样本空间，为了对不同的样本空间区分，我们便将其记为S，你也可以记为其他的符号，如S 1 、S 2 等。
  接下来引入事件的概念：实验E的样本空间S的子集为E的随机事件，简称事件。通俗点说，就是实验E中任意结果的组合就可以是一个事件。拿我们的例子来说，它的事件可以是事件A：“第一次出现的是正面H”，那我们就来找实验结果中所有第一出现是H的实验结果，可以得到A={HHH, HHT, HTH, HTT}。再举个例子，它的事件也可以是事件B：“三次都是正面”，这个事件只有一个实验结果｛HHH｝。
  说了这么多，终于可以解释随机变量的概念了：设实验的样本空间为S={e}，X=X(e)是定义在样本空间S上的实值单值函数，称X=X{e}为随机变量。我们还是用例子来解释概念，对于实验E，我们有S={HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}，假设用X(e)记三次投掷硬币得到正面H的次数，此处你可以理解为X(e)的每一种取值都表示一个事件，那么一共有四种取值，代表了四种事件，分别为‘三次都为正面’值为3，‘有两次为正面’值为2，有一次为正面’值为1和‘三次都为反面’值为0。为了简写，用X表示X(e)，我们可以将X写成：

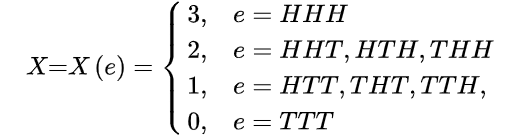
  有了随机变量X，我们就可以轻松的用符号表示出诸如求三次投掷得到正面H的总数大于1的概率，即P{X>1}，答案为1/2，因为从上面式子可以清楚的看出大于1的实验结果有4种分别为{HHH, HHT, HTH, THH}，占总数的一半。

注解：以上概念中的‘实验’皆指代随机实验，只是为了便于概念的通俗化，写作了实验。

参考资料：

1. 浙江大学概率论与数理统计第四版

微信公众号

  欢迎大家关注微信公众号鼓励我继续分享知识！~~

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！