Android 陀螺仪与图像坐标系处理
Android 陀螺仪与图像坐标系处理
最近在做项目的时候需要处理陀螺仪和摄像头两个传感器,并将其对齐,在这里记录一下处理过程。仅是个人理解,如有错误,欢迎批评指正。
1 陀螺仪坐标系与图像坐标
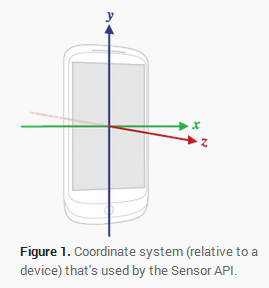
首先,Android手机中的陀螺仪的坐标方向如上图所示,在写程序时调用的监听器可以获得到的陀螺仪信息event.value[0],event.value[1],event.value[2]分别对应陀螺仪的x,y,z轴。
那么如何与手机拍摄到的图像进行匹配呢。
首先如果我们向上图那样竖着拿手机,拍摄到的图片如果在程序中不进行任何的旋转,则会得到如下方向的图片。

如果将手机横过来:

则拍摄到的是和看到的相同方向的图片:

这表明,从摄像头中获取到的图片就是该方向的图片,对于CMOS摄像头,图像是从上向下进行刷新的。
关于相机的拍摄方向:
-
无论如何摆放手机,拍摄出的画面总是和你看到的是一致的,之所以会出现获取到的图片与你看到的不一致的现象,是因为设备自动将图片旋转了
-
摄像头有一个默认的取景方向,手机一般是横屏放置,也就是竖着拿手机时,面向手机屏幕,摄像头的上边缘与手机边框的右边缘平行,从背面看就是下图:

-
横屏拍摄时,摄像头是正的,所见即所得,而手机竖过来,拍摄到的景物与你看到的是一致的,但是摄像头是以横屏为基准,则默认将其逆时针旋转了90度
-
无论如何,相机的刷新方向都应该看摄像头的方向,也就是如果正放摄像头,则是从上到下一行一行刷新,也就是在手机上显示正确的图片都是从右向左一列一列刷新
为了便于描述,下面以手机横过来时的情况作为基准,可以得到:

其中,蓝色坐标系为手机陀螺仪坐标系,橙色坐标系为我们自己假设的图像坐标系,那么可以得到如下关系:
pic_x = gyro_y;
pic_y = -gyro_x;
pic_z = gyro_z;
在获取陀螺仪角速度时可以将其直接按照上述关系进行保存,方便后续对图像的计算,也就是说,我们成功将陀螺仪的坐标系转化为图像上坐标系。
2 陀螺仪的数据处理
这里假设我们从陀螺仪中读取到的值都是较为精准的(这里暂时不考虑需要滤波的问题)。
对陀螺仪的数据处理分为两部分:
- 将陀螺仪的角速度信息转化为旋转矩阵
- 确保此旋转矩阵描述的是该帧图像(与图像的对齐问题)
2.1 陀螺仪->旋转矩阵
由于陀螺仪获取到的是角速度信息,在实际应用中,我们需要将其转化为可以描述物体旋转的旋转矩阵(这里使用李群so(3))(一定要注意左右手坐标系!!坑了我好久)
首先是李群so(3)的计算,这里放下代码:
cv::Mat ThetaHelper::getRotationMat(cv::Vec theta)
{cv::Mat cvmat(3, 3, CV_64F);cv::Mat skew_mat(3, 3, CV_64F);int eq=0;double th=theta[0]*theta[0]+theta[1]*theta[1]+theta[2]*theta[2];th=sqrt(th);if(th==0)eq=1;th=th+eq;theta[0]=theta[0]/th;theta[1]=theta[1]/th;theta[2]=theta[2]/th;//计算旋转矩阵skew_mat.at(0,0)=0;skew_mat.at(0,1)=theta[2];skew_mat.at(0,2)=-theta[1];skew_mat.at(1,0)=-theta[2];skew_mat.at(1,1)=0;skew_mat.at(1,2)=theta[0];skew_mat.at(2,0)=theta[1];skew_mat.at(2,1)=-theta[0];skew_mat.at(2,2)=0;cv::Mat e=cv::Mat::eye(3,3,CV_64F);cvmat =e+sin(th)*skew_mat.t()+(1-cos(th))*(skew_mat*skew_mat).t();return cvmat;
}
由于需要将获取到的图片通过OpenGL ES渲染到手机屏幕上,而OpenGL ES使用的是右手坐标系,所以获取旋转矩阵时需要计算右手坐标系。
2.2 陀螺仪与图像对齐
获取到旋转矩阵后,要解决的一个问题就是如何确保旋转矩阵确实是对该帧图片的描述。究其根源,其实就是对于时间戳的一个对齐。
首先要将图像时间戳和陀螺仪的时间戳转换到同一个时间体系中,这里都将其转化到RTC时间体系。
但是这样还不够,由于每帧图像只有一个时间戳,而我们仅能在获取到该帧图像后打上时间戳,一个本能的处理方式是:计算相邻两帧图像时间戳之间陀螺仪三轴的旋转角度
这里附上代码,仅供参考:
cv::Vec ThetaHelper::getTheta()
{cv::Vec theta;//该帧的三轴角度for(int i=0; i0){double lastftime= Timeframe[findex - 1];theta[0]=lastx*(gtime-lastftime)+lastt[0];theta[1]=lasty*(gtime-lastftime)+lastt[1];theta[2]=lastz*(gtime-lastftime)+lastt[2];}while(gtime 具体思路为:
假设当前陀螺仪时间戳为 t g c t_{gc} tgc
比较当前帧时间戳 t f t_f tf和下一帧陀螺仪时间戳 t g n t_{gn} tgn大小:
-
如果 t g n t_{gn} tgn< t f t_f tf,则使用 t g c t_{gc} tgc 乘以( t g n t_{gn} tgn- t g c t_{gc} tgc)作为当前时间段的变化角度
-
如果 t g n t_{gn} tgn> t f t_f tf,则使用 t g c t_{gc} tgcc乘以( t g n t_{gn} tgn- t f t_f tf)作为当前时间段的变化角度
-
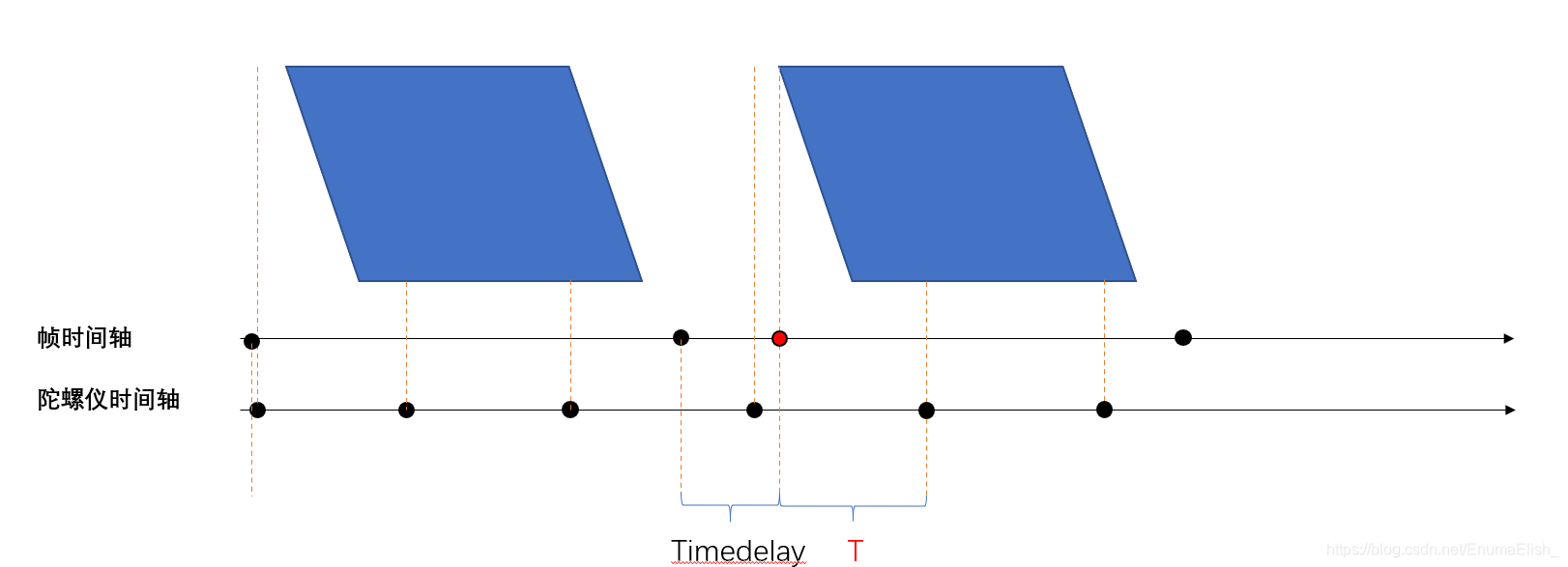
在进行到下一个图像帧时,还要加上上一图像帧时间戳到相对于该图像的第一个陀螺仪时间戳这个时间段内(T)的变化角度。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wsgYym4L-1590243875192)(Android 陀螺仪与图像坐标系处理.assets/image-20200523205738202.png)]
但这还不够,由于是在获取图像后才打上的帧时间戳(即帧时间轴上两个黑点),无法从陀螺仪获取到的角度是对该帧的准确描述(如果开始的地方不对齐导致旋转矩阵与帧有时间差),故如果将上一帧时间戳与下一图像帧开始时刻对齐,则可以确保陀螺仪数据是从一帧图像的开始进行描述。而尾部多出来的一部分角度在实际使用的时候可以忽略不计。具体做法是在使用时对帧时间戳加上一个常量timedelay,该常量的计算可以通过一些特殊的标定手段得到。
陀螺仪获取到的角度是对该帧的准确描述(如果开始的地方不对齐导致旋转矩阵与帧有时间差),故如果将上一帧时间戳与下一图像帧开始时刻对齐,则可以确保陀螺仪数据是从一帧图像的开始进行描述。而尾部多出来的一部分角度在实际使用的时候可以忽略不计。具体做法是在使用时对帧时间戳加上一个常量timedelay,该常量的计算可以通过一些特殊的标定手段得到。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!