KD树构建---kd树的三维代码和二维代码C++

1、三维空间点代码：

1、kdtree.h

/*** @file   kdtree.h* @brief Thisis a brief description.* @author dongjian* @par   Copyright (c):*         All Rights Reserved* @date   2018:04:24 *  @note   mattersneeding attention*/  
#ifndef _5383BD42_370E_4C00_A25E_AD4403E5656A
#define _5383BD42_370E_4C00_A25E_AD4403E5656A
#include 
#include 
#include namespace kdtree
{class Point //空间中的三维点{public:double x;double y;double z;// 末尾const的作用是 不会改变本类对象中的实例成员变量double Distance(const Point& p) const;// 有参构造函数。Point(double ox, double oy, double oz);void printPoint(){std::cout << "最近点：("<< this->x << "," << this->y << "," << this->z << ")"<<std::endl;}};class BBox{public:double xmin, ymin, zmin;double xmax, ymax, zmax;bool Contains(const Point& p) const;bool Contains(const BBox& bbox) const;// 相交的意思bool Intersects(const BBox& bbox) const;BBox(double x0, double x1, double y0, double y1, double z0, double z1);// 静态函数，返回值是BBoxstatic BBox UniverseBBox();double ShortestDistance(const Point& p) const;};enum Dimension{X = 0,Y = 1,Z = 2};class Node{public:Node* left;			//left childNode* right;		//right childint begin;			//start index [closeint end;				//end index  (openDimension dimension;	//cut dimensiondouble pivot;		//cut valueNode(int b, int e, Dimension dim, double piv);bool IsLeaf() const;// 左子叶信封 什么鬼？BBox LeftSubTreeEnvelope(const BBox& current_entext) const;BBox RightSubTreeEnvelope(const BBox& current_entext) const;};class KDTree{public:// 设置输入，构建树void SetInput(const std::vector<Point>& inputs);// 搜索void RangeSearch(const BBox& bbox, std::vector<int>& indices) const ;int NearestNeighbourSearch(const Point& searchpoint) const ;void  NearestNeighbourSearch(const Point& searchpoint, int k, std::vector<int>& indices) const;static int _leaf_max_size;private:const std::vector<Point>* pData; // 2维数组std::vector<int> indices;Node* pRoot;private:struct comparepair{bool operator()(const std::pair<int, double>&, const std::pair<int, double>&);};typedef std::priority_queue<std::pair<int, double>, std::vector<std::pair<int, double>>, comparepair> index_distance;Node* DivideTree(const std::vector<Point>& inputs,int start,int end);Dimension SelectDimension(const std::vector<Point>& inputs, int start, int end);int Partition(int start, int end, Dimension dim);double GetAt(int index, Dimension dim);void _range_search(const BBox& search_bbox, Node* pNode, const BBox& current_extent,std::vector<int>& indices) const ;int _nearest_neighbour(const Point& searchPoint, Node* pNode, const BBox& current_extent, double& current_shorest_dis) const ;void _nearest_neighbour(const Point& searchPoint, int k, index_distance& ins, Node* pNode, const BBox& current_extent, double& current_shorest_dis) const ;};}
#endif //_5383BD42_370E_4C00_A25E_AD4403E5656A

2、kdtree.cpp 含demo实现

#include "kdtree.h"
#include 
#include 
#include 
using namespace std;
using namespace kdtree;Point::Point(double ox, double oy, double oz) :
x(ox),
y(oy),
z(oz)
{}double Point::Distance(const Point& p) const
{double dx = p.x - x;double  dy = p.y - y;double dz = p.z - z;return sqrt(dx*dx + dy*dy + dz*dz);
}BBox Node::LeftSubTreeEnvelope(const BBox& current_entext) const
{BBox leftRegion(current_entext);switch (dimension){case X:leftRegion.xmax = pivot;break;case Y:leftRegion.ymax = pivot;break;case Z:leftRegion.zmax = pivot;break;}return leftRegion;
}BBox Node::RightSubTreeEnvelope(const BBox& current_entext) const
{BBox rightRegion(current_entext);switch (dimension){case X:rightRegion.xmin = pivot;break;case Y:rightRegion.ymin = pivot;break;case Z:rightRegion.zmin = pivot;break;}return rightRegion;
}bool BBox::Contains(const BBox& bbox) const
{if (bbox.xmin < xmin)		return false;if (bbox.xmax > xmax)		return false;if (bbox.ymin < ymin)		return false;if (bbox.ymax < ymax)		return false;if (bbox.zmin < zmin)		return false;if (bbox.zmax > zmax)		return false;return true;
}bool BBox::Contains(const Point& p) const
{return p.x >= xmin && p.x <= xmax && p.y >= ymin && p.y <= ymax&& p.z >= zmin && p.z <= zmax;
}bool BBox::Intersects(const BBox& bbox) const
{if (bbox.xmin > xmax || bbox.xmax < xmin) return false;if (bbox.ymin > xmax || bbox.ymax < ymin) return false;if (bbox.zmin > zmax || bbox.zmax < zmin) return false;return true;
}BBox BBox::UniverseBBox()
{double DOUBLE_MAX = std::numeric_limits<double>::max();return BBox(-DOUBLE_MAX, DOUBLE_MAX, -DOUBLE_MAX, DOUBLE_MAX, -DOUBLE_MAX, DOUBLE_MAX);
}BBox::BBox(double x0, double x1, double y0, double y1, double z0, double z1) :
xmin(x0),
xmax(x1),
ymin(y0),
ymax(y1),
zmin(z0),
zmax(z1)
{}double BBox::ShortestDistance(const Point& p) const
{double dx = xmin - p.x > 0 ? xmin - p.x : (p.x - xmax > 0 ? p.x - xmax : 0);double dy = ymin - p.y > 0 ? ymin - p.y : (p.y - ymax > 0 ? p.y - ymax : 0);double dz = zmin - p.z > 0 ? zmin - p.z : (p.z - zmax > 0 ? p.z - zmax : 0);return sqrt(dx*dx + dy*dy + dz*dz);
}Node::Node(int b, int e, Dimension dim, double piv) :
begin(b),
end(e),
dimension(dim),
pivot(piv),
left(nullptr),
right(nullptr)
{}bool Node::IsLeaf() const
{return left == nullptr && right == nullptr;
}
// 选择维度？
/*** @brief * * @param inputs 输入原始数据 * @param start 起始索引* @param end * @return Dimension  输入的数据中，在x y z轴上哪个跨度大，就输出哪个枚举类型*/
Dimension KDTree::SelectDimension(const std::vector<Point>& inputs, int start, int end)
{struct cmpobj{Dimension dim;cmpobj(Dimension d) :dim(d){}bool operator()(const Point& p0, const Point p1) const{if (dim == X)return p0.x < p1.x;if (dim == Y)return p0.y < p1.y;if (dim == Z)return p0.z < p1.z;return false;}};// span存的是最大－最小值double span[3];// 该pair 的first指向[first,last)范围内最小值元素，second指向最大值元素。auto pair =  std::minmax_element(inputs.begin() + start, inputs.begin() + end,cmpobj(X));span[0] = pair.second->x - pair.first->x;pair = std::minmax_element(inputs.begin() + start, inputs.begin() + end, cmpobj(Y));span[1] = pair.second->y - pair.first->y;pair = std::minmax_element(inputs.begin() + start, inputs.begin() + end, cmpobj(Z));span[2] = pair.second->z - pair.first->z;// 获得的索引是 span里面最大元素与第一个元素之间的距离，也就是获得最大元素的索引。auto index = std::distance(span, std::max_element(span, span + 3));return static_cast<Dimension>(index);
}double KDTree::GetAt(int index, Dimension dim)
{auto p = (*pData)[indices[index]];return  dim == X ? p.x : (dim == Y ? p.y : p.z);
}int KDTree::Partition(int start, int end, Dimension dimension)
{int size = end - start;if (size <= 0){cout << "a serious error occurs " << start << "\t" << endl;return -1;}struct cmpobj{Dimension dim;const std::vector<Point>* pData;bool operator()(int i, int j) const {if (X == dim)return (*pData)[i].x < (*pData)[j].x;if (Y == dim)return (*pData)[i].y < (*pData)[j].y;if (Z == dim)return (*pData)[i].z < (*pData)[j].z;return true;}cmpobj(Dimension dimension, const std::vector<Point>* pInputData):dim(dimension),pData(pInputData){}};int median = start +size / 2;std::nth_element(indices.begin() + start, indices.begin()+median , indices.begin() + end, cmpobj(dimension, pData));return median;
}int KDTree::NearestNeighbourSearch(const Point& searchpoint) const 
{double shortestDistance = std::numeric_limits<double>::max();return _nearest_neighbour(searchpoint, pRoot, BBox::UniverseBBox(), shortestDistance);
}void KDTree::NearestNeighbourSearch(const Point& searchpoint, int k, std::vector<int>& indices) const 
{double shortestDistance = std::numeric_limits<double>::max();indices.clear();index_distance neighbours;_nearest_neighbour(searchpoint, k, neighbours, pRoot, BBox::UniverseBBox(), shortestDistance);while (!neighbours.empty()){indices.push_back(neighbours.top().first);neighbours.pop();}
}bool KDTree::comparepair::operator()(const std::pair<int, double>& p0, const std::pair<int, double>& p1)
{return p0.second < p1.second;
}void KDTree::_nearest_neighbour(const Point& searchPoint, int k, index_distance& ins,Node* pNode, const BBox& current_extent, double& current_shorest_dis) const 
{double min_shortest_distance = current_extent.ShortestDistance(searchPoint);if (min_shortest_distance >= current_shorest_dis)return;if (pNode->IsLeaf()){for (auto i = pNode->begin; i < pNode->end; ++i){double distance = (*pData)[indices[i]].Distance(searchPoint);if (ins.size() < k){ins.push(pair<int, double>(indices[i], distance));	//add elementif (k == ins.size())current_shorest_dis = ins.top().second;}else {if (distance < current_shorest_dis){ins.pop();ins.push(pair<int, double>(indices[i], distance));//add elementcurrent_shorest_dis = ins.top().second;}}}}else{BBox leftRegion = pNode->LeftSubTreeEnvelope(current_extent);BBox rightRegion = pNode->RightSubTreeEnvelope(current_extent);double dis_to_left = leftRegion.ShortestDistance(searchPoint);double dis_to_right = rightRegion.ShortestDistance(searchPoint);if (dis_to_left < dis_to_right){_nearest_neighbour(searchPoint,k,ins,pNode->left,leftRegion,current_shorest_dis);_nearest_neighbour(searchPoint, k,ins,pNode->right, rightRegion, current_shorest_dis);}else{_nearest_neighbour(searchPoint,k,ins, pNode->right, rightRegion, current_shorest_dis);_nearest_neighbour(searchPoint,k,ins, pNode->left, leftRegion, current_shorest_dis);}}
}int KDTree::_nearest_neighbour(const Point& searchPoint, Node* pNode, const BBox& current_extent, double& current_shorest_dis) const 
{double min_shortest_distance = current_extent.ShortestDistance(searchPoint);if (min_shortest_distance >= current_shorest_dis)return -1;if (pNode->IsLeaf()){int shortestindex =-1;for (auto i = pNode->begin; i < pNode->end;++i){double distance = (*pData)[indices[i]].Distance(searchPoint);if (distance < current_shorest_dis){shortestindex = indices[i];current_shorest_dis = distance;}}return shortestindex;}else{BBox leftRegion = pNode->LeftSubTreeEnvelope(current_extent);BBox rightRegion = pNode->RightSubTreeEnvelope(current_extent);double dis_to_left = leftRegion.ShortestDistance(searchPoint);double dis_to_right = rightRegion.ShortestDistance(searchPoint);if (dis_to_left < dis_to_right){int left = _nearest_neighbour(searchPoint, pNode->left, leftRegion, current_shorest_dis);int right = _nearest_neighbour(searchPoint, pNode->right, rightRegion, current_shorest_dis);return right == -1 ? left : right;}else{int right = _nearest_neighbour(searchPoint, pNode->right, rightRegion, current_shorest_dis);int left = _nearest_neighbour(searchPoint, pNode->left, leftRegion, current_shorest_dis);return left == -1 ? right : left;}return -1;}
}int KDTree::_leaf_max_size = 2; //原来是15void KDTree::SetInput(const std::vector<Point>& inputs)
{pData = &inputs;// 指针的首地址 指向了inputs的地址indices.resize(inputs.size());for (int i = 0, n = inputs.size(); i < n; ++i)indices[i] = i;// 1 2 3 4 5 6 ....// Node类型的指针pRoot = DivideTree(inputs, 0, inputs.size()); //划分树
}Node* KDTree::DivideTree(const std::vector<Point>& inputs, int start, int end)
{//cout << "build " << start << "\t" << end << endl;int size = end - start;if (size <= 0)return nullptr;Dimension dim = SelectDimension(inputs, start, end); // 选择划分维度，是按X轴划分还是y轴还是z轴// 中位数int median = Partition(start, end, dim); //获取中位数Node* pNode = new Node(start, end, dim, GetAt(median, dim));//递归终止条件是输入的点的个数小于叶子节点最大点个数if (size > _leaf_max_size){pNode->left = DivideTree(inputs, start, median);pNode->right = DivideTree(inputs, median, end);}return pNode;
}void KDTree::RangeSearch(const BBox& bbox, std::vector<int>& indices) const 
{BBox universe_bbox = BBox::UniverseBBox();_range_search(bbox, pRoot, universe_bbox, indices);
}void KDTree::_range_search(const BBox& search_bbox, Node* pNode, const BBox& current_extent, std::vector<int>& ins) const 
{if (nullptr == pNode)return;if (pNode->IsLeaf()){for (int i = pNode->begin; i < pNode->end; ++i){const Point& p = (*pData)[indices[i]];if (search_bbox.Contains(p))ins.push_back(indices[i]);}}else{//trim bounding boxBBox leftRegion = pNode->LeftSubTreeEnvelope(current_extent);if (search_bbox.Contains(leftRegion)){for (int i = pNode->left->begin; i < pNode->left->end; ++i)ins.push_back(indices[i]);}else if (search_bbox.Intersects(leftRegion)){_range_search(search_bbox, pNode->left, leftRegion, ins);}BBox rightRegion = pNode->RightSubTreeEnvelope(current_extent);if (search_bbox.Contains(rightRegion)){for (int i = pNode->right->begin; i < pNode->right->end; ++i)ins.push_back(indices[i]);}else if (search_bbox.Intersects(rightRegion)){_range_search(search_bbox, pNode->right, rightRegion, ins);}}
}
int main(int argc, char *argv[]){std::vector<kdtree::Point> input;// 1、输入数据for (int  i = 0; i < 10; i++){double x,y,z;std::cin>>x>>y>>z;std::cout<<x<<y<<z<<std::endl;kdtree::Point p(x, y, z);input.push_back(p);}//2、构建树KDTree kdtree;kdtree.SetInput(input);//3、最近邻搜索//创建寻找的点int k =3;Point p1(1.2 , 2.1, 3.2);std::vector<int> indices;//索引kdtree.NearestNeighbourSearch(p1, k, indices);//4、打印K个最近点for(int i = 0; i<k; i++ ){input[indices[i]].printPoint();std::cout << "距离是：" << p1.Distance(input[indices[i]]) << std::endl;}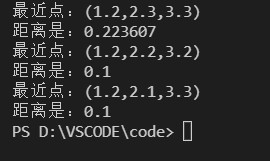return 0;
}

结果：

2、二维空间代码

1、kdtree_new.h

//
//  KDTree.h
//  Test
//
//  Created by xiuzhu on 2021/7/13.
//#ifndef kdtree_new_h
#define kdtree_new_h#include using namespace std;
//template 
class KDTree {
private:int key;vector<double> root;//树及其子树的根节点KDTree *parent;KDTree *left_child;KDTree *right_child;public:KDTree();~KDTree();bool is_empty();//判断KD树是否为空bool is_leaf();//判断树是否只有一个叶子节点bool is_root();//判断是否是树的根节点bool is_left();//判断该子kd树的根结点是否是其父kd树的左结点bool is_right();//判断该子kd树的根结点是否是其父kd树的右结点vector<vector<double> > Transpose(const vector<vector<double> > &Matrix);//坐标转换double findMiddleValue(vector<double> vec);//查找中指void buildKdTree(KDTree* tree, vector<vector<double> > data, unsigned depth);//构建kd树void printKdTree(KDTree* tree, unsigned int depth);//逐层打印KD树double measureDistance(vector<double> point1, vector<double> point2, unsigned method);//计算空间中两个点的距离vector<double> searchNearestNeighbor(vector<double> goal, KDTree *tree);在kd树tree中搜索目标点goal的最近邻};#endif /* KDTree_h */

2、kdtree_new.cpp

//
//  KDTree.cpp
//  Test
//
//  Created by xiuzhu on 2021/7/13.
//
#include "kdtree_new.h"
#include 
#include 
#include 
#include 
#include 
#include using namespace std;KDTree::KDTree():parent(nullptr),left_child(nullptr),right_child(nullptr){}
KDTree::~KDTree(){}
bool KDTree::is_empty()
{return root.empty();
}
bool KDTree::is_leaf()
{return (!root.empty()) && right_child == nullptr && left_child == nullptr;
}
bool KDTree::is_root()
{return (!is_empty()) && parent == nullptr;
}
bool KDTree::is_left()
{return parent->left_child->root == root;
}
bool KDTree::is_right()
{return parent->right_child->root == root;
}
//用于转换坐标
vector<vector<double> > KDTree::Transpose(const vector<vector<double>> &Matrix)
{unsigned row = Matrix.size();unsigned col = Matrix[0].size();vector<vector<double> > Trans(col,vector<double>(row,0));for (unsigned i = 0; i < col; ++i){for (unsigned j = 0; j < row; ++j){Trans[i][j] = Matrix[j][i];}}return Trans;
}
//在不同的坐标轴上寻找中值double KDTree::findMiddleValue(vector<double> vec)
{sort(vec.begin(),vec.end());auto pos = vec.size() / 2;return vec[pos];
}
void KDTree::buildKdTree(KDTree *tree, vector<vector<double>> data, unsigned int depth)
{//样本的数量unsigned long samplesNum = data.size();//终止条件if (samplesNum == 0){return;}if (samplesNum == 1){tree->root = data[0];return;}//样本的维度unsigned long k = data[0].size();//坐标轴个数vector<vector<double> > transData = Transpose(data);//选择切分属性unsigned splitAttribute = depth % k;vector<double> splitAttributeValues = transData[splitAttribute];//选择切分值double splitValue = findMiddleValue(splitAttributeValues);//cout << "splitValue" << splitValue  << endl;// 根据选定的切分属性和切分值，将数据集分为两个子集vector<vector<double> > subset1;vector<vector<double> > subset2;for (unsigned i = 0; i < samplesNum; ++i){if (splitAttributeValues[i] == splitValue && tree->root.empty())tree->root = data[i];else{if (splitAttributeValues[i] < splitValue)subset1.push_back(data[i]);elsesubset2.push_back(data[i]);}}//子集递归调用buildKdTree函数tree->left_child = new KDTree;tree->left_child->parent = tree;tree->right_child = new KDTree;tree->right_child->parent = tree;buildKdTree(tree->left_child, subset1, depth + 1);buildKdTree(tree->right_child, subset2, depth + 1);
}
void KDTree::printKdTree(KDTree *tree, unsigned int depth)//打印
{for (unsigned i = 0; i < depth; ++i)cout << "\t";for (vector<double>::size_type j = 0; j < tree->root.size(); ++j)cout << tree->root[j] << ",";cout << endl;if (tree->left_child == nullptr && tree->right_child == nullptr )//叶子节点return;else //非叶子节点{if (tree->left_child != nullptr){for (unsigned i = 0; i < depth + 1; ++i)cout << "\t";cout << " left:";printKdTree(tree->left_child, depth + 1);}cout << endl;if (tree->right_child != nullptr){for (unsigned i = 0; i < depth + 1; ++i)cout << "\t";cout << "right:";printKdTree(tree->right_child, depth + 1);}cout << endl;}
}
//计算空间中两个点的距离
double KDTree::measureDistance(vector<double> point1, vector<double> point2, unsigned int method){if (point1.size() != point2.size()){cerr << "Dimensions don't match！！" ;exit(1);}switch (method){case 0://欧氏距离{double res = 0;for (vector<double>::size_type i = 0; i < point1.size(); ++i){res += pow((point1[i] - point2[i]), 2);}return sqrt(res);}case 1://曼哈顿距离{double res = 0;for (vector<double>::size_type i = 0; i < point1.size(); ++i){res += abs(point1[i] - point2[i]);}return res;}default:{cerr << "Invalid method!!" << endl;return -1;}}}
//在kd树tree中搜索目标点goal的最近邻
//输入：目标点；已构造的kd树
//输出：目标点的最近邻
vector<double> KDTree::searchNearestNeighbor(vector<double> goal, KDTree *tree)
{/*第一步：在kd树中找出包含目标点的叶子结点：从根结点出发，递归的向下访问kd树，若目标点的当前维的坐标小于切分点的坐标，则移动到左子结点，否则移动到右子结点，直到子结点为叶结点为止,以此叶子结点为“当前最近点”*/unsigned long k = tree->root.size();//计算出数据的维数unsigned d = 0;//维度初始化为0，即从第1维开始KDTree* currentTree = tree;vector<double> currentNearest = currentTree->root;while(!currentTree->is_leaf()){unsigned index = d % k;//计算当前维if (currentTree->right_child->is_empty() || goal[index] < currentNearest[index]){currentTree = currentTree->left_child;}else{currentTree = currentTree->right_child;}++d;}currentNearest = currentTree->root;/*第二步：递归地向上回退， 在每个结点进行如下操作：(a)如果该结点保存的实例比当前最近点距离目标点更近，则以该例点为“当前最近点”(b)当前最近点一定存在于某结点一个子结点对应的区域，检查该子结点的父结点的另一子结点对应区域是否有更近的点（即检查另一子结点对应的区域是否与以目标点为球心、以目标点与“当前最近点”间的距离为半径的球体相交）；如果相交，可能在另一个子结点对应的区域内存在距目标点更近的点，移动到另一个子结点，接着递归进行最近邻搜索；如果不相交，向上回退*///当前最近邻与目标点的距离double currentDistance = measureDistance(goal, currentNearest, 0);//如果当前子kd树的根结点是其父结点的左孩子，则搜索其父结点的右孩子结点所代表//的区域，反之亦反KDTree* searchDistrict;if (currentTree->is_left()){if (currentTree->parent->right_child == nullptr)searchDistrict = currentTree;elsesearchDistrict = currentTree->parent->right_child;}else{searchDistrict = currentTree->parent->left_child;}//如果搜索区域对应的子kd树的根结点不是整个kd树的根结点，继续回退搜索while (searchDistrict->parent != nullptr){//搜索区域与目标点的最近距离double districtDistance = abs(goal[(d+1)%k] - searchDistrict->parent->root[(d+1)%k]);//如果“搜索区域与目标点的最近距离”比“当前最近邻与目标点的距离”短，表明搜索//区域内可能存在距离目标点更近的点if (districtDistance < currentDistance )//&& !searchDistrict->isEmpty(){double parentDistance = measureDistance(goal, searchDistrict->parent->root, 0);if (parentDistance < currentDistance){currentDistance = parentDistance;currentTree = searchDistrict->parent;currentNearest = currentTree->root;}if (!searchDistrict->is_empty()){double rootDistance = measureDistance(goal, searchDistrict->root, 0);if (rootDistance < currentDistance){currentDistance = rootDistance;currentTree = searchDistrict;currentNearest = currentTree->root;}}if (searchDistrict->left_child != nullptr){double leftDistance = measureDistance(goal, searchDistrict->left_child->root, 0);if (leftDistance < currentDistance){currentDistance = leftDistance;currentTree = searchDistrict;currentNearest = currentTree->root;}}if (searchDistrict->right_child != nullptr){double rightDistance = measureDistance(goal, searchDistrict->right_child->root, 0);if (rightDistance < currentDistance){currentDistance = rightDistance;currentTree = searchDistrict;currentNearest = currentTree->root;}}}//end ifif (searchDistrict->parent->parent != nullptr){searchDistrict = searchDistrict->parent->is_left()?searchDistrict->parent->parent->right_child:searchDistrict->parent->parent->left_child;}else{searchDistrict = searchDistrict->parent;}++d;}//end whilereturn currentNearest;
}const int data[6][2]={{2,3},{5,4},{9,6},{4,7},{8,1},{7,2}};
int main()
{vector<vector<double> > train(6, vector<double>(2, 0)); // 初始化为6个 值为（2,0）的坐标for (unsigned i = 0; i < 6; ++i)for (unsigned j = 0; j < 2; ++j)train[i][j] = data[i][j];KDTree* kdTree = new KDTree();kdTree->buildKdTree(kdTree, train, 0);kdTree->printKdTree(kdTree, 0);vector<double> goal;goal.push_back(4);goal.push_back(6);vector<double> nearestNeighbor = kdTree->searchNearestNeighbor(goal, kdTree);vector<double>::iterator beg = nearestNeighbor.begin();cout << "The nearest neighbor is: ";while(beg != nearestNeighbor.end()) cout << *beg++ << ",";cout << endl;return 0;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！