钢条的最优切割问题

问题描述：

一家公司购买长钢条，将其切割成短钢条出售，假设切割本身没有成本，长度为i的短钢条的价格为Pi。那给定一段长度为n的钢条和一个价格表Pi，求钢条的切割方案使得收益Rn最大。

举一个例子来说：

例如某公司以单价26元买到了一批长度为10的钢条，目前各长度钢条的市场价如下表所示：

要求：

随机生成钢条长度n和不同长度钢条的价格信息，编写程序确定一种钢条的切割方案，使公司的收益最大化。

动态规划：
对于长度为n的钢条，我们可以先切一刀，切下长度为1-10的钢条，共10种切法，
最大收益就是切下的钢条收益和剩下钢条的最大收益之和。

钢条长度为1的最大收益计算出来，保存到r[1]

长度为2的钢条，遍历每一种切法，收益最大的保存到r[2]

计算长度为n的钢条的最大收益，此时r数组已经保存了1——n-1长度钢条的最大收益
遍历这10种切法，就可以找到最大的收益

由于每种钢条长度的最大收益都被保存在数组r中，避免了很多的重复计算

设计思路：

对于一个动态规划问题：

第一步先确定最优解的结构。如果一个问题的解结构包含其子问题的最优解，就称此问题具有最优子结构性质。使用动态规划算法时，用子问题的最优解来构造原问题的最优解。因此必须考查最优解中用到的所有子问题。

第二步定义最优解的计算公式

第三步根据得到的求最优解公式，计算出结果。

第四步构造出最优解。

算法设计：

首先生成随机价格，将不同长度的钢条价格生成，然后通过算法去计算最优解，即最优切割问题的最优解，得到最高价格。

代码：

#include 
#include 
#include 
int N[11]={};//存储价格 
int r[11]={};
int upToDown(int);
int maxx(int a,int b);
int main()
{	int z,x,c,a[11]={0};printf("钢条长度:"); for(z=0;z<=10;z++)printf("%3d",z);//随机数生成，生成不同钢条长度的不同价格 srand((unsigned)time(NULL));for(z=0;z<=10;z++){a[z]=rand()%(25)+4;}printf("\n");for(z=0;z<=9;z++)for(x=z+1;x<=10;x++){if(a[z]>a[x]){c=a[z];a[z]=a[x];a[x]=c;}}a[0]=0;a[1]=1,a[2]=4,a[3]=7;printf("钢条价格:");for(z=0;z<=10;z++)N[z]=a[z];for(z=0;z<=10;z++)printf("%3d",a[z]);//对钢条进行切割计算				int current;puts("\n输入你要裁剪的钢条长度：");scanf("%d",¤t);int i;printf("%d长的钢条最大收益是：%d\n",current,upToDown(current));printf("各个长度的收益情况：\n长度：");for(i=0;i<=current;i++){printf("%3d ",i);}printf("\n");printf("收益：");for(i=0;i<=current;i++){printf("%3d ",r[i]);}
} 
int upToDown(int n) //每次返回的值是当前长度n的最大收益 
{if(n==0)return 0;int q=N[n];	int i;for(i=1;i=b)return a;elsereturn b;
}

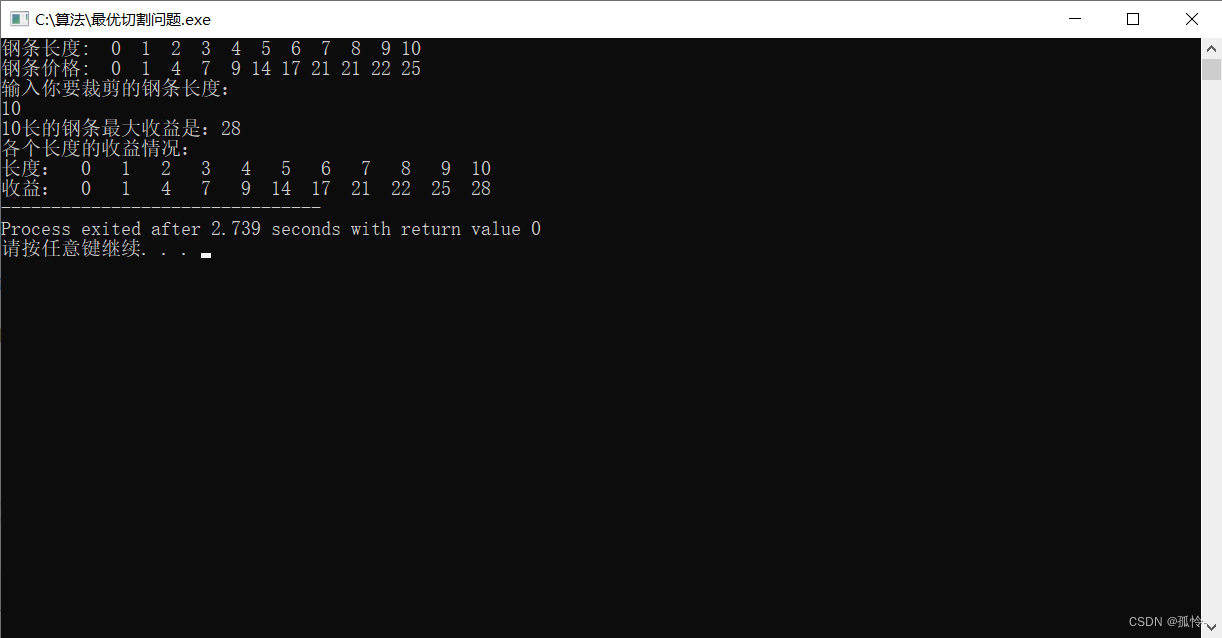
算法求解：

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！