群的基本概念-抽象代数【密码学数学基础】
什么是群
群为什么叫群，群（group）这个术语最早由Galois引入，他使用这个词仅仅表示它是元素的聚集。现在的抽象群是Galois的群概念的推广。群是抽象的概念，是代数学中最基本的代数结构，群是由一个集合以及一个二元运算所组成。
群的定义
设G是一个非空集合，·是它的一个二元运算，群必须满足以下条件：
若群G中元素个数是有限的，则G称为有限群（有限群的元素个数称为有限群的阶），否则称为无限群。
例如：
群的性质
（1）
（2）
（3）
（4） 
定理一：群里的单位元是唯一的
证明：反证法
假设存在两个单位元 e,e'∈G且e≠e'
而
，与假设矛盾，故群里的单位元是唯一的。
定理二：每个元素只有唯一的逆元
证明：假设存在元素a属于G，a有不相等的逆元b和c
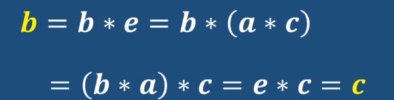
故每个元素只有唯一的逆元
群的简记符号（易混淆）
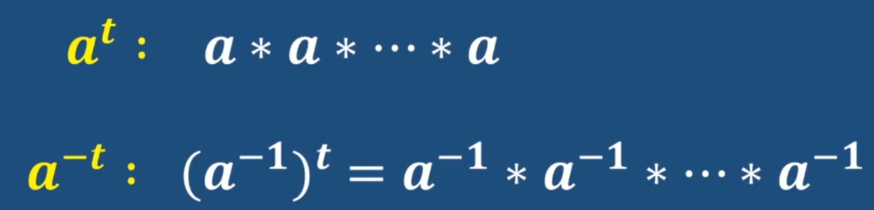
阿贝尔群（Abel group）
群乘：将集合中的任意两个元素构成唯一的另一个元素的运算。群乘不一定是代数运算中的乘法，也不一定满足交换律。
阿贝尔群又称交换群
下面将介绍阿贝尔群的定理
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！