神经网络语言模型 -- Neural Network Language Model

背景

2003年，Bengio首次提出Neural Network Language Model(NNLM), 开创了神经网络运用在语言模型的先河，论文 《A Neural Probabilistic Language Model》
上一章提到传统的统计语言模型的缺点，在高维的情况下，由于N元组的稀疏问题，传统的语言模型需要花大量时间解决平滑，插值等问题；N受限于算力，不大的时候文本的长距离依赖关系无法进行建模；同时N元组共现未必相似等问题。

模型介绍

针对这些传统语言模型的问题，NNLM尝试用三层神经网络进行建模

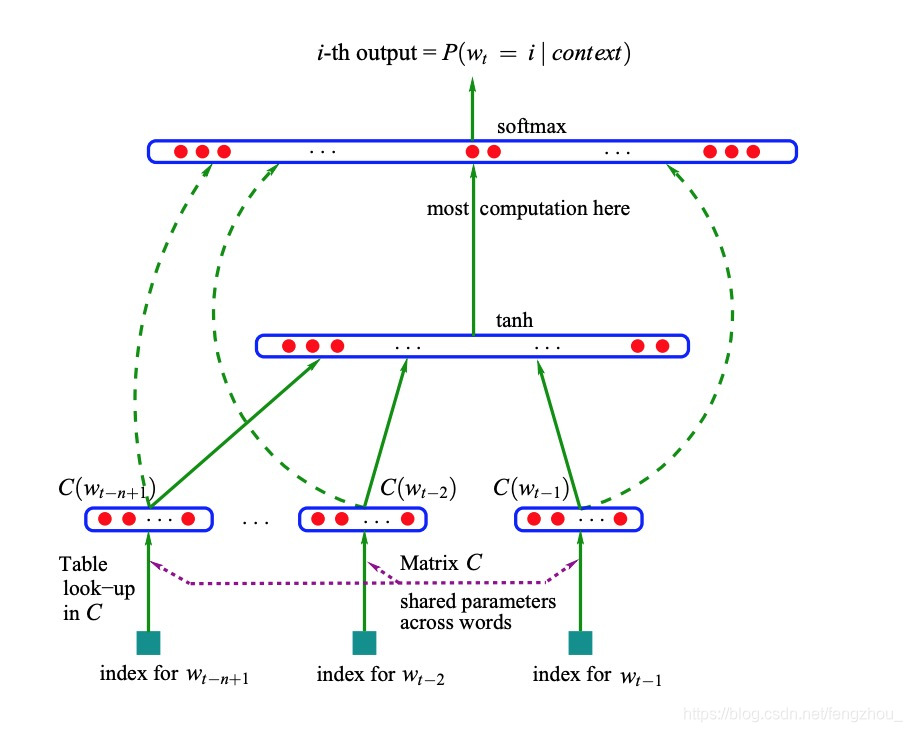
如图所示，整个模型有三层

第一层是输入层：模型的输入 w t − n + 1 ⋯ w t − 2 , w t − 1 w_{t-n+1}{\cdots}w_{t-2},w_{t-1} wt−n+1​⋯wt−2​,wt−1​表示n-1个词，目标是预测当前t时刻的 w t w_t wt​，模型引入词向量（Word Vector）的概念，将输入的词通过look-up table映射成为一个n-1个向量，这里我们假设词典大小$|V|$, 向量的维度为$d$, look-up table C的为$V\cdot d$的矩阵，将N-1个向量concat起来，输入层维度为$(n-1)\cdot d$的向量，这里记为$x$

第二层是隐藏层，通过一个fully connect layer传递，神经元的激活函数是tanh，参数 W h W_{h} Wh​为$(n-1)\cdot d\ast h$的矩阵，输出为 t a n h ( W h ⋅ x + b h ) tanh(W_h{\sdot}x+b_h) tanh(Wh​⋅x+bh​)，维度大小为h

第三层是输出层，依赖隐藏层的输出和输入层的输出之和 U ⋅ t a n h ( W h ⋅ x + b h ) + W o ⋅ x + b o U{\sdot}tanh(W_h{\sdot}x+b_h) +W_o{\sdot}x+b_o U⋅tanh(Wh​⋅x+bh​)+Wo​⋅x+bo​, 其中 W o W_o Wo​为$V\ast d\cdot (n-1)$的矩阵, $U$为$V\ast h$的矩阵，这里输出的向量维度为$V$，再通过softmax函数，每个神经元的节点即为t时刻出现第i个词的概率 P ( w t i ∣ w t − n + 1 ⋯ w t − 2 , w t − 1 ) P(w_t^i|w_{t-n+1}{\cdots}w_{t-2},w_{t-1}) P(wti​∣wt−n+1​⋯wt−2​,wt−1​)

模型的参数 θ = ( U , W h , b h , W 0 , b o ) \theta=(U, W_h, b_h, W_0, b_o) θ=(U,Wh​,bh​,W0​,bo​), 参数总数为$|V|(1+nd+h)+h(1+(n-1)d)$, 其中d为look-up表C的维度， h为隐藏层维度， V为词表大小，n-1为输入层的输入的词的个数

模型的损失函数loss function为
L = 1 T ∑ t l o g f ( w t , w t − 1 , ⋯ , w t − n + 1 ; θ ) + R ( θ ) (1) L=\frac{1}{T}\sum_tlogf(w_t,w_{t-1},{\cdots},w_{t-n+1};\theta) + R(\theta) \tag1 L=T1​t∑​logf(wt​,wt−1​,⋯,wt−n+1​;θ)+R(θ)(1)
其中 f ( w t , w t − 1 , ⋯ , w t − n + 1 ; θ ) f(w_t,w_{t-1},{\cdots},w_{t-n+1};\theta) f(wt​,wt−1​,⋯,wt−n+1​;θ)为概率 P ( w t ∣ w t − n + 1 ⋯ w t − 2 , w t − 1 ) P(w_t|w_{t-n+1}{\cdots}w_{t-2},w_{t-1}) P(wt​∣wt−n+1​⋯wt−2​,wt−1​), $R(\theta )$为正则项，其中 P ( w t ∣ w t − n + 1 ⋯ w t − 2 , w t − 1 ) = e y w t ∑ i V e y i P(w_t|w_{t-n+1}{\cdots}w_{t-2},w_{t-1})=\frac{e^{y_{wt}}}{\sum_i^Ve^{yi}} P(wt​∣wt−n+1​⋯wt−2​,wt−1​)=∑iV​eyieywt​​, 即softmax后的概率，通过反向传播公式优化算法即可得到模型参数$\theta$

优点

1. 相比传统的统计语言模型，Ngram的N增加只带来线性提升，而非指数复杂的提升
2. 通过高维空间连续稠密的词向量解决统计语言模型中解决稀疏（sparse）的问题，不用进行平滑等操作
3. 另外词向量的引入解决统计语言模型部分相似性的问题，为后续NLP词向量时代的发展做铺垫
4. 相比传统的统计语言模型，神经网络的非线性能力获得更好的泛化能力，perplexity（困惑度提升）

困惑度

困惑度（perplexity）的基本思想是：给测试集的句子赋予较高概率值的语言模型较好,当语言模型训练完之后，测试集中的句子都是正常的句子，那么训练好的模型就是在测试集上的概率越高越好，公式如下：
P P ( W ) = P ( w 1 w 2 ⋯ w N ) − 1 N = 1 P ( w 1 w 2 ⋯ w N ) N (2) PP(W) = P(w_1w_2{\cdots}w_N)^{-\frac{1}{N}}=\sqrt[N]{\frac{1}{P(w_1w_2{\cdots}w_N)}} \tag2 PP(W)=P(w1​w2​⋯wN​)−N1​=NP(w1​w2​⋯wN​)1​ ​(2)
由公式可知，句子概率越大，语言模型越好，迷惑度越小。

缺点

参数较多，部分计算复杂，在word2vec等后续模型中陆续优化

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！