Learning to Reason Deductively: Math Word Problem Solving as Complex Relation Extraction翻译

摘要

解决数学单词问题需要对文本中的数值进行演绎推理。最近的各种研究工作主要依赖于序列到序列或序列到树模型，以生成数学表达式，而无需在给定上下文的情况下显示执行数值之间的关系推理。尽管这在经验上是有效的，但这种方法通常并未为生成的表达提供合理解释。在这项工作中，我们将任务视为一个复杂的关系提取问题，并提出了一种新的方法，该方法提出了可解释的演绎推理步骤，以迭代方式构建目标表达式，其中每个步骤涉及定义两个数值上的基本操作，以作为它们的关系。通过在四个基准数据集上进行的大量实验表明，我们提出的模型显着优于现有的强基线。我们进一步证明，演绎过程不仅生成了可解释的步骤，而且还使能够对需要更复杂推理的问题进行更准确的预测。

1.介绍

　　数学单词问题（MWP）是求解由自然语言描述的数学问题的任务。解决MWP需要对上下文中出现的数值进行逻辑推理，以计算数值答案。最近的各种研究工作将该问题视为生成问题，通常，此类模型着重于生成完整的目标数学表达，通常以线性序列或树结构的形式表示。
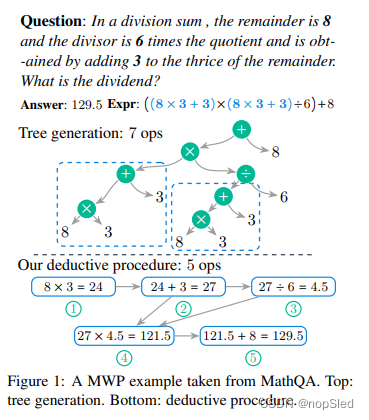
　　图1（顶部）描述了一种经典的方法，该方法试图以树结构的形式生成目标表达式，这是在最近的研究工作中采用的。具体而言，输出是可以从这种生成结构中获得的表达式。我们注意到，树结构的生成具有几个局限性。首先，这种结构通常在生成时涉及特定的顺序。在示例中，将加法（“+”）操作作为生成的第一步，这一决定可能是违反直觉的，并且没有提供足够的解释，以向人类学习者展示这一推理过程。此外，所得树包含相同的子树（“8×3+3”），如蓝色虚线中所示。除非引入某种专门设计的机制来重用已经生成的中间表达式，否则该方法将需要在其生成相同子表达的过程中重复相同的工作。
　　解决数学单词问题通常需要演绎推理，这也被认为是儿童认知发展中的重要能力之一。在这项工作中，我们提出了一种新的方法，该方法明确提出了演绎推理步骤。我们观察到，从根本上可以将MWP求解看作是一个复杂的关系提取问题，即确定给定问题文本中出现数值之间复杂关系的任务。每个基本算术操作（例如加法，减法）基本上定义了不同类型的关系。通过利用最近在文献中有关关系抽取任务的成功，我们提出的方法涉及一个迭代过程，该过程反复在两个选择的数值（包括新生成的数值）之间进行关系提取。
　　如图1所示，我们的方法直接提取8和3之间的关系（“乘法”或“×”），该关系来自“余数为8”和“余数的三倍”的上下文。此外，它使我们能够在第四步中重复中间表达式的结果。这个过程自然产生了演绎推理过程，从现有知识中得出了新知识。设计这样的复杂关系提取系统具有一些实际的挑战。例如，某些数量可能与问题无关，而其他一些数量可能需要多次使用。 该模型还需要学习如何正确处理从中间表达式中出现的新数量。学习如何有效搜索最佳操作序列（关系）以及何时停止演绎过程也很重要。
　　在这项工作中，我们做出了以下几个主要贡献：

• 我们将MWP求解作为一个复杂关系提取任务，我们旨在反复确定不同数值之间的基本关系。据我们所知，这是从新的角度成功解决MWP的第一个尝试。
• 我们的模型能够自动生成可解释的步骤，从而得到最终答案，并具有演绎推理过程。
• 我们在两种语言的四个标准数据集上的实验结果表明，我们的模型大大优于现有的强基线。我们进一步表明，该模型在具有更复杂方程式的问题上的性能要比以前的方法更好。

2.相关工作

早期工作的重点是使用手工制作的概率模型来解决MWP。Roy and Roth (2018) 设计了模板方法以发现声明语言和方程式之间的对齐方式。最近的工作通过使用基于序列或树的生成模型来解决该问题。 Wang et al. (2017) 提出了Math23k数据集，并提出了一种序列到序列（seq2seq）的方法来生成数学表达式。其他方法通过强化学习，基于模板的方法和组注意力机制改善了seq2seq模型。Xie and Sun (2019) 提出了一个目标驱动的树结构（GTS）模型来生成表达树。这种序列到树的方法可显着改善传统的seq2seq方法的性能。一些后续工作结合了外部知识，例如句法依存或常识知识。Cao et al. (2021) 将方程式建模为有向无环图以获得表达式。Zhang et al. (2020) and Li et al. (2020) 使用图卷积网络（GCN）对数值关系进行建模。预训练的语言模型（例如BERT）的应用被证明可显着受益于树的表达式生成。
　　与基于树的生成模型不同，我们的工作与演绎系统有关，我们旨在逐步生成表达式。最近的工作也一直在朝着这一方向发展。Ling et al. (2017) 构建了一个数据集，以提供对每个步骤表达式的解释。Amini et al. (2019) 创建了用分步操作标注的MathQA数据集，该标注提供了解决问题所需的每个中间步骤表达式。我们的演绎过程（图1）试图以增量的，分步的方式自动获得表达式。
　　我们的方法还与关系提取（RE）有关，这是信息提取领域的基本任务，该任务侧重于确定一对实体之间的关系。最近，Zhong and Chen (2021) 设计了一种简单有效的方法，可以直接对跨度表示的关系进行建模。在这项工作中，我们将一对数值之间的操作视为我们演绎推理过程中每个步骤的关系。传统方法应用了基于规则的方法来提取数学关系。
　　MWP求解通常被视为system 2任务之一，我们当前针对该问题的解决方法与神经符号推理有关。我们在模型（第3.2节）中设计可微分模块以在数值之间执行推理。

3.方法

数学单词问题求解任务可以定义如下。给定一个由$n$个单词列表组成的问题描述 S = { w 1 , w 2 , ⋯ , w n } \mathcal S=\{w_1,w_2,⋯,w_n\} S={w1​,w2​,⋯,wn​}，其中$\mathcal{S}$包含$m$个数值 Q S = { q 1 , q 2 , . . . , q m } \mathcal Q_S=\{q_1,q_2,...,q_m\} QS​={q1​,q2​,...,qm​}，我们的任务是解决问题并返回数值答案。理想情况下，答案应通过一系列基本数学操作进行数学推理过程计算，如图1所示。这些操作可以包括“+”（加法），“ - ”（减法），“×”（乘法）， “÷”（除法）和“ **”（指数）。
　　我们认为，上面的每个基本数学操作基本上都可以用于描述数值之间的特定关系。从根本上讲，解决数学单词问题是一个复杂关系提取的问题，这要求我们反复确定数值之间的关系（包括出现在文本中的数值和中间步骤构建的数值）。总体求解过程需要在每个步骤中调用关系分类模块，从而产生演绎推理过程。
　　实际上，如果不依赖某些可能没有出现在给定的问题描述中的预定义常数（例如$\pi$和1），某些问题事无法回答的。 因此，我们还考虑了一组常数 C = { c 1 , c 2 , ⋯ , c ∣ C ∣ } \mathcal C=\{c_1,c_2,⋯,c_{|\mathcal C|}\} C={c1​,c2​,⋯,c∣C∣​}。 此类常数也被认为是数值（即，它们被视为 { q m + 1 , q m + 2 , . . . , q m + ∣ C ∣ } \{q_{m+1},q_{m+2},...,q_{m+|\mathcal C|}\} {qm+1​,qm+2​,...,qm+∣C∣​}），这些常数在构建最终表达式时可能会扮演重要的角色。

3.1 A Deductive System

　　如图1所示，在两个数量之间应用数学关系（例如“+”）产生了中间表达式$e$。通常，在步骤$t$，计算后的结果表达式 e ( t ) e^{(t)} e(t)成为新创建的数值，并被添加到候选数值列表中，并在步骤$t+1$参与剩余的演绎推理过程。该过程可以在数学上表示如下：

• Initialization：
  Q = Q S ∪ C \mathcal Q=\mathcal Q_{S}\cup \mathcal C Q=QS​∪C
• At step $t$：
  e i , j , o p ( t ) = q i → o p q j q i , q j ∈ Q ( t − 1 ) Q ( t ) = Q ( t − 1 ) ∪ { e i , j , o p ( t ) } q ∣ Q ( t ) ∣ : = e i , j , o p ( t ) \begin{array}{cc} e^{(t)}_{i,j,op}=q_i\stackrel{op}{\rightarrow} q_j\quad q_i,q_j\in \mathcal Q^{(t-1)}\\ \mathcal Q^{(t)}=Q^{(t-1)}\cup \{e^{(t)}_{i,j,op}\}\\ q_{|\mathcal Q^{(t)}|}:=e^{(t)}_{i,j,op} \end{array} ei,j,op(t)​=qi​→opqj​qi​,qj​∈Q(t−1)Q(t)=Q(t−1)∪{ei,j,op(t)​}q∣Q(t)∣​:=ei,j,op(t)​​

其中 e i , j , o p ( t ) e^{(t)}_{i,j,op} ei,j,op(t)​代表将关系$op$应用于有序对 ( q i , q j ) (q_i,q_j) (qi​,qj​)后的表达式。遵循标准归纳系统，推理过程如图2所示。我们从具有数值列表 Q ( 0 ) \mathcal Q^{(0)} Q(0)的公理开始。如上所述，推断规则是 q i → o p q j q_i\stackrel{op}{\rightarrow} q_j qi​→opqj​，以在步骤$t$处获得新数值。

3.2 Model Components

　　（1）Reasoner
　　图3显示了我们模型中的归纳推理过程，其中涉及3个数值。我们首先将数值（例如2088）转换为一个数值字符“$<quant>$”。接下来，我们采用预训练的语言模型，例如BERT或Roberta，以获取每个数值$q$的数值表示$\text{q}$。
　　给定数值表示，我们考虑所有可能的数值对 ( q i , q j ) (q_i,q_j) (qi​,qj​)。与Lee et al. (2017)类似，我们可以通过拼接两个数值表示和它们之间的逐元素乘来获得每对的最终表示。如图3所示，我们在对表示的顶部应用非线性前馈网络（FFN），以获取新创建的表达式的表示。上述过程可以在数学上写为：
e i , j , o p = F F N o p ( q i , q j , q i ∘ q j ) , i ≤ j (1) \textbf e_{i,j,op}=FFN_{op}(\textbf q_i,\textbf q_j,\textbf q_i\circ \textbf q_j),i\le j\tag{1} ei,j,op​=FFNop​(qi​,qj​,qi​∘qj​),i≤j(1)
其中 e i , j , o p \textbf e_{i,j,op} ei,j,op​是中间表达式$e$的表示，$op$是应用于有序对 ( q i , q j ) (q_i,q_j) (qi​,qj​)的操作（例如“+”，“ - ”）。 F F N o p FFN_{op} FFNop​是一个指定操作的网络，在指定操作$op$下提供表达式表示。请注意，我们给定了约束$i\le j$。同时，我们还考虑了除法和减法的“反向操作”。
　　如图3所示，表达式 e 1 , 2 , ÷ e_{1,2,÷} e1,2,÷​将被视为$t=1$时的新数值表示。通常，我们可以将分数分配给单个推理步骤，从而产生基于操作$op$的 q i q_i qi​和 q j q_j qj​的表达式 e i , j ( t ) e^{(t)}_{i,j} ei,j(t)​。可以通过对在两个数值表示上定义的分数和在表达式上定义的分数进行求和来得到最终分数：
s ( e i , j , o p ( t ) ) = s q ( q i ) + s q ( q j ) + s e ( e i , j , o p ) (2) s(e^{(t)}_{i,j,op})=s_q(\textbf q_i)+s_q(\textbf q_j)+s_e(\textbf e_{i,j,op})\tag{2} s(ei,j,op(t)​)=sq​(qi​)+sq​(qj​)+se​(ei,j,op​)(2)
其中，我们有：
s q ( q i ) = w q ⋅ F F N ( q i ) s e ( e i , j , o p ) = w e ⋅ e i , j , o p (3) \begin{array}{cc} s_q(\textbf q_i)=\textbf w_q\cdot FFN(\textbf q_i)\\ s_e(\textbf e_{i,j,op})=\textbf w_e\cdot \textbf e_{i,j,op} \end{array}\tag{3} sq​(qi​)=wq​⋅FFN(qi​)se​(ei,j,op​)=we​⋅ei,j,op​​(3)
其中 s q ( ⋅ ) s_q(\cdot) sq​(⋅)和 s e ( ⋅ ) s_e(\cdot) se​(⋅)分别为分配给数值和表达式的得分， w q \textbf w_q wq​和 w e \textbf w_e we​是相应的可学习参数。我们的目标是找到最佳表达序列 [ e ( 1 ) , e ( 2 ) , ⋯ , e ( T ) ] [e^{(1)},e^{(2)},⋯,e^{(T)}] [e(1),e(2),⋯,e(T)]，使我们能够计算最终的数值答案，其中$T$是此演绎过程所需的步骤总数 。
　　（2）Terminator
　　我们的模型还具有一种机制，该机制可以决定是否在任何给定时间终止演绎过程。我们引入了一个二元标签$\tau$，其中1表示该过程在此处停止，否则为0。因此，在时间步骤$t$时表达式$e$的最终分数可以计算为：
S ( e i , j , o p ( t ) , τ ) = s ( e i , j , o p ( t ) ) + w τ ⋅ F F N ( e i , j , o p ) (4) S(e^{(t)}_{i,j,op},\tau)=s(e^{(t)}_{i,j,op})+\textbf w_{\tau}\cdot FFN(\textbf e_{i,j,op})\tag{4} S(ei,j,op(t)​,τ)=s(ei,j,op(t)​)+wτ​⋅FFN(ei,j,op​)(4)
其中 w τ \textbf w_{\tau} wτ​是评分$\tau$的参数向量。
　　（3）Rationalizer

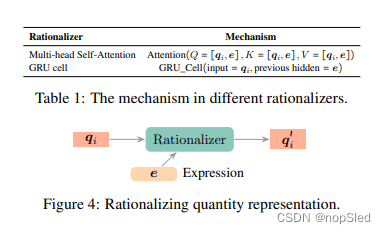
　　一旦我们在步骤$t$获得了新的中间表达式，那么对现有数值的表示进行更新是非常重要的。我们之所以称之为rationalization，是因为它有可能为我们提供合理的解释结果。如图4所示，中间表达$\text{e}$充当解释数值从$\text{q}$到 q ′ \textbf q' q′的理由。没有此步骤，该模型将存在潜在缺陷。也就是说，因为如果我们继续进行演绎推理过程，且数值表示不进行更新，那么最初排名的表达式（例如，在第一步）将始终比那些在整个过程中排名低的表达式优先。我们使用当前的中间表达式 e ( t ) e^{(t)} e(t)来更新数值表示，以便该数值在更新后会了解到生成的表达式。该过程可以在数学上表达如下：
q i ′ = R a t i o n a l i z e r ( q i , e ( t ) ) ∀ 1 ≤ i ≤ ∣ Q ∣ (5) \textbf q'_i=Rationalizer(\textbf q_i,\textbf e^{(t)})\quad \forall 1\le i\le |\mathcal Q|\tag{5} qi′​=Rationalizer(qi​,e(t))∀1≤i≤∣Q∣(5)
　　我们可以采用的两种知名技术来更新数值表示，即多头自注意力和一个门控循环单元（GRU）。 表1显示了两个的更新机制。对于第一种方法，我们从本质上构建了一个带有两个字符表示的句子（数值 q i \textbf q_i qi​和表达式$\text{e}$），以执行自注意力。在第二种方法中，我们将 q i \textbf q_i qi​用作输入，$\text{e}$作为GRU单元中先前的隐藏状态。

3.3 Training and Inference

与训练sequence-to-sequence模型相似，我们采用了teacher-forcing策略来指导模型在训练过程中使用golden表达式。 损失可以写为：
L ( θ ) = ∑ t = 1 T ( m a x ( i , j , o p ) ∈ H ( t ) , τ [ S θ ( e i , j , o p ( t ) , τ ) ] − S θ ( e i ∗ , j ∗ , o p ∗ ( t ) , τ ∗ ) ) + λ ∣ ∣ θ ∣ ∣ 2 (6) \mathcal L(\textbf θ)=\sum^T_{t=1}\bigg(\mathop{max}\limits_{(i,j,op)\in \mathcal H^{(t)},\tau}\bigg[\mathcal S_{\textbf θ}(e^{(t)}_{i,j,op},\tau)\bigg]-\mathcal S_{\textbf θ}(e^{(t)}_{i^*,j^*,op^*},\tau^*)\bigg)+\lambda ||\textbf θ||^2\tag{6} L(θ)=t=1∑T​((i,j,op)∈H(t),τmax​[Sθ​(ei,j,op(t)​,τ)]−Sθ​(ei∗,j∗,op∗(t)​,τ∗))+λ∣∣θ∣∣2(6)
其中$\text{θ}$包含演绎推理器中的所有参数，而 H ( t ) \mathcal H^{(t)} H(t)包含时刻$t$所有可能的数值对和关系选择。$\lambda$是 L 2 L_2 L2​正则化项的超参数。集合 H ( t ) \mathcal H^{(t)} H(t)随着新表达式的构建而增加，并在演绎推理过程中添加新数值。总体损失是通过对每个时间步骤的损失进行求和来计算的。
　　在推理期间，我们设置一个最大时间步长 T m a x T_{max} Tmax​，并找到在每个时间步中具有最高分数的最佳表达式 e ∗ e^∗ e∗。一旦选择了$\tau =1$，我们就停止构建新表达式并终止该过程。总体表达式（由结果表达式序列形成）将用于计算最终数值答案。
　　Declarative Constraints。我们的模型重复依靠现有数值来构建新数值，从而导致显示的演绎推理过程。这种方法的一个优点是，它允许方便地纳入某些声明性知识。例如，正如我们在等式6中看到的那样，默认方法考虑了最大化步骤中数量之间的所有可能组合。我们可以轻松地施加约束，以避免考虑某些组合。实际上，我们在某些数据集（例如SVAMP）中发现，没有任何应用于相同数量操作的表达式（例如9 + 9或9×9，其中9来自文本中的相同数量）。此外，我们还观察到中间结果不会为负。我们可以简单地在最大化过程中排除此类案例，从而有效地减少训练和推理期间的搜索空间。我们表明，添加此类声明性约束可以帮助提高性能。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！