杨辉三角问题ⅠⅡ

文章目录

• 1.Leetcode118 杨辉三角Ⅰ
• • 题目描述
  • 思路分析+代码实现
  • • 动态规划法
    • 递归法
• 2.Leetcode119 杨辉三角Ⅱ
• • 题目描述
  • 思路分析+代码实现

1.Leetcode118 杨辉三角Ⅰ

题目描述

给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。

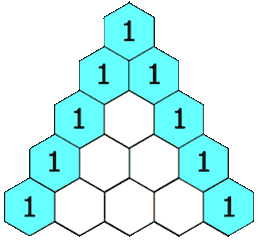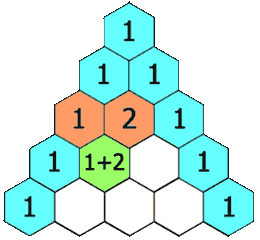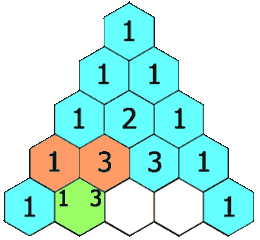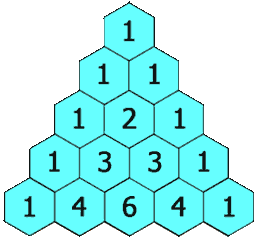
在杨辉三角中，每个数是它左上方和右上方的数的和。

思路分析+代码实现

动态规划法

如果能够知道一行杨辉三角，我们就可以根据每对相邻的值轻松地计算出它的下一行。
虽然这一算法非常简单，但用于构造杨辉三角的迭代方法可以归类为动态规划，因为我们需要基于前一行来构造每一行。

首先，我们会生成整个 triangle 列表，三角形的每一行都以子列表的形式存储。然后，我们会检查行数为 000 的特殊情况，否则我们会返回 [1]。如果 numRows>0，那么我们用 [1] 作为第一行来初始化 triangle with [1]，并按如下方式继续填充：

代码实现：

// 动态规划法public static List<List<Integer>> generate1(int numRows) {List<List<Integer>> triangle = new ArrayList<List<Integer>>();// 第一步：如果行数为0，直接返回if (numRows == 0) {return triangle;}// 第二步：设置第0行元素为1triangle.add(new ArrayList<Integer>());triangle.get(0).add(1);for (int rowNum = 1; rowNum < numRows; rowNum++) {// 创建新的一行List<Integer> row = new ArrayList<Integer>();// 找出这一行的上一行List<Integer> prevRow = triangle.get(rowNum - 1);// 这一行第一个元素为1row.add(1);for (int i = 1; i < rowNum; i++) {row.add(prevRow.get(i - 1) + prevRow.get(i));}// 每一行最后一个元素都为1row.add(1);triangle.add(row);}return triangle;}

递归法

递归方法总而言之就是抓住三点：

1.找整个递归的终止条件
2.找返回值
3.一次递归需要如何操

代码实现：

public static List<List<Integer>> generate(int numRows) {// 存储要返回的杨辉三角List<List<Integer>> list = new ArrayList<List<Integer>>();// 若0行，则返回空if (numRows == 0) {return list;}// 递归出口，这是第一步！找到出口if (numRows == 1) {list.add(new ArrayList<Integer>());list.get(0).add(1);return list;}// 递归，注意返回值！！！这是第二步list = generate(numRows - 1);// 一级递归要做啥，我们可以看第二行到第三行需要做啥// 首先是要申请一个list来存储第三行，然后通过第二行得到第三行// 第三行的首尾为1是确定了的，然后就是中间的数如何得到// 通过观察很容易拿到for循环里面的式子// 最后别忘了返回值List<Integer> row = new ArrayList<Integer>();row.add(1);// numRows-1行有numRows-1个元素，其中第一个和最后一个为1，j < numRows-1表示中间还能添加多少个元素for (int j = 1; j < numRows - 1; j++) {row.add(list.get(numRows - 2).get(j - 1) + list.get(numRows - 2).get(j));}row.add(1);list.add(row);return list;}

2.Leetcode119 杨辉三角Ⅱ

题目描述

给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。

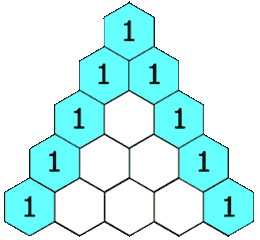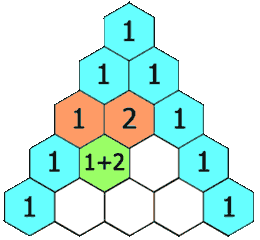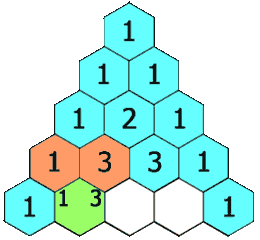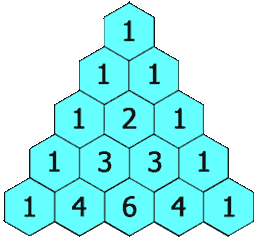
在杨辉三角中，每个数是它左上方和右上方的数的和。

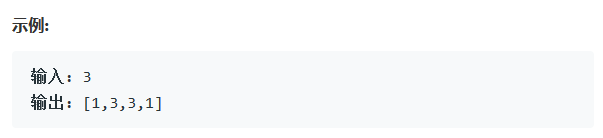
思路分析+代码实现

公式法一：
首先我们应该了解杨辉三角正好是二次项的展开式,(1+x)的n次幂的系数,
有通项公式C(n-1,m-1)=(n-1)!/[(m-1)!(n-m)!]
而研究每一项后,发现他们的规律,如
C(4,1)=C(4,0)*4/1,
C(4,2)=C(4,1)*3/2,
C(4,3)=C(4,2)*2/3,
C(4,4)=C(4,3)*1/4:

public static List<Integer> getRow(int rowIndex) {List<Integer> res = new ArrayList<Integer>(rowIndex + 1);int k=1;for (int i = 0; i <= rowIndex; i++) {res.add(k);k=k*(rowIndex-i)/(i+1);}return res;}

公式法二：

// 公式法2// C(n,k)​=n!/(k!(n−k)!)=(n∗(n−1)∗(n−2)∗...(n−k+1))/k!public static List<Integer> getRow2(int rowIndex) {List<Integer> ans = new ArrayList<Integer>();int N = rowIndex;for (int k = 0; k <= N; k++) {ans.add(Combination(N, k));}return ans;}private static int Combination(int N, int k) {long res = 1;for (int i = 1; i <= k; i++) {res = res * (N - k + i) / i;}return (int) res;}

优化版：

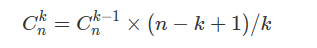
	public static List<Integer> getRow3(int rowIndex) {List<Integer> ans=new ArrayList<Integer>();int N=rowIndex;long pre=1;ans.add(1);for (int k = 1; k <=N; k++) {long cur=pre*(N-k+1)/k;ans.add((int)cur);pre=cur;}return ans;}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！