成考数学四-一元函数微分学-导数与微分

导数

1、导数的概念
1.函数在一点处的导数定义
定义：设函数$y=f(x)$在 x 0 x_0 x0​及其附近有定义，如果极限 lim ⁡ x → x 0 f ( x ) − f ( x 0 ) x − x 0 { \lim\limits_{x \to x_0}} \dfrac{f(x)-f(x_0)}{x-x_0} x→x0​lim​x−x0​f(x)−f(x0​)​存在，则称函数$f(x)$在 x = x 0 x = x_0 x=x0​处可导，极限的值称为函数$f(x)$在 x = x 0 x = x_0 x=x0​处的导数，记作 f ′ ( x 0 ) f^ ′(x_0) f′(x0​)， 𝑦 ′ ∣ 𝑥 = 𝑥 0 𝑦^′| 𝑥=𝑥_0 y′∣x=x0​， d y d x ∣ x = x 0 \dfrac{dy}{dx}|x=x_0 dxdy​∣x=x0​或 d f ( x ) d x ∣ x = x 0 \dfrac{df(x)}{dx}|x=x_0 dxdf(x)​∣x=x0​等.
记 ∆ x ＝ x − x 0 ∆x ＝ x − x_0 ∆x＝x−x0​， ∆ f ( x 0 ) = f ( x 0 + ∆ x ) － f ( x 0 ) ∆f(x_0)=f(x_0+∆x)－f(x_0) ∆f(x0​)=f(x0​+∆x)－f(x0​)，导数定义可表述为：
若极限 lim ⁡ ∆ x → 0 ∆ f ( x 0 ) ∆ x { \lim\limits_{∆x \to 0}} \dfrac{∆f(x_0)}{∆x} ∆x→0lim​∆x∆f(x0​)​存在，则称函数$f(x)$在 x = x 0 x = x_0 x=x0​处可导，极限的值称为函数$f(x)$在 x = x 0 x = x_0 x=x0​处的导数.
极限值 lim ⁡ ∆ x → 0 ∆ f ( x 0 ) ∆ x { \lim\limits_{∆x \to 0}} \dfrac{∆f(x_0)}{∆x} ∆x→0lim​∆x∆f(x0​)​，即导数值 𝑓 ′ ( x 0 ) 𝑓^′(x_0) f′(x0​)，称为函数$f(x)$在 x 0 x_0 x0​处的变化率， ∣ 𝑓 ′ ( x 0 ) ∣ | 𝑓^′(x_0)| ∣f′(x0​)∣的大小反映了$f(x)$在 x 0 x_0 x0​处函数值随着自变量变化而变化的快慢， 𝑓 ′ ( 𝑥 0 ) 𝑓^′(𝑥_0) f′(x0​)的正、负号反映的是函数值随着自变量的增加是增加还是减小.
2.函数在一点处的单侧导数
定义：设函数$f(x)$在 x 0 x_0 x0​及其左侧附近有定义，如果极限 lim ⁡ x → x 0 − f ( x ) − f ( x 0 ) x − x 0 { \lim\limits_{x \to x_0^-}} \dfrac{f(x)-f(x_0)}{x-x_0} x→x0−​lim​x−x0​f(x)−f(x0​)​存在，则称函数$f(x)$在 𝑥 = x 0 𝑥=x_0 x=x0​处左可导，极限的值称为函数$f(x)$在 𝑥 = x 0 𝑥=x_0 x=x0​处的左导数，记作 f − ′ ( x 0 ) f^′_- (x0) f−′​(x0).
同理，可以定义函数$f(x)$在 𝑥 = x 0 𝑥=x_0 x=x0​处的右导数，记作 f + ′ ( x 0 ) f^′_+ (x_0) f+′​(x0​).
定理：设函数 $y=f(x)$在 x 0 x_0 x0​及其附近有定义，则$f(x)$在 x 0 x_0 x0​处可导，且 f ′ ( x 0 ) = A f^ ′(x_0) = A f′(x0​)=A 的充分必要条件是： $f(x)$在 x 0 x_0 x0​处既是左可导的，又是右可导的，且 f − ′ ( x 0 ) = f + ′ ( x 0 ) = A f^′_- (x_0) = f^′_+ (x_0) = A f−′​(x0​)=f+′​(x0​)=A.
当函数$f(x)$在区间(𝑎, 𝑏)内的每一点都可导时，就说它在区间(𝑎, 𝑏)内可导， 𝑓 ′ ( 𝑥 ) 𝑓^′(𝑥) f′(x)称为$f(x)$在区间(𝑎, 𝑏)内的导函数.
当函数$f(x)$在区间(a, b)内的每一点都可导，且在$x=a$处右可导,在$x=b$处左可导时，就说它在区间[a, b]上可导， f ′ ( x ) f ^′(x) f′(x)也称为$f(x)$在区间[a, b]上的导函数.
3.函数在一点处导数的几何意义
f ′ ( x 0 ) f^′(x_0) f′(x0​)表示的是曲线$y=f(x)$在点 ( x 0 , f ( x 0 ) ) (x_0,f(x_0)) (x0​,f(x0​))处切线的斜率，所以曲线$y=f(x)$在点 ( x 0 , f ( x 0 ) ) (x_0,f(x_0)) (x0​,f(x0​))处的切线方程
𝐲 = 𝐟 ( 𝐱 𝟎 ) + 𝐟 ′ ( 𝐱 𝟎 ) ( 𝐱 − 𝐱 𝟎 ) 𝐲 = 𝐟(𝐱_𝟎) + 𝐟^′(𝐱_𝟎)(𝐱 − 𝐱_𝟎) y=f(x0​)+f′(x0​)(x−x0​)
过切点且与曲线在该点的切线垂直的直线称为曲线在该点的法线，当 f ′ ( x 0 ) ≠ 0 f^′(x_0) \neq 0 f′(x0​)=0 时，曲线$y=f(x)$在点 ( x 0 , f ( x 0 ) ) (x_0,f(x_0)) (x0​,f(x0​))处的法线方程
𝐲 = 𝐟 ( 𝐱 𝟎 ) − 1 𝐟 ′ ( 𝐱 𝟎 ) ( 𝐱 − 𝐱 𝟎 ) 𝐲 = 𝐟(𝐱𝟎) − \dfrac{1}{𝐟^′(𝐱_𝟎)} (𝐱 − 𝐱_𝟎) y=f(x0)−f′(x0​)1​(x−x0​)
两条曲线在点 ( x 0 , y 0 ) (x_0,y_0) (x0​,y0​)处相切指它们在该点的切线重合，即它们在 x 0 x_0 x0​处函数值和导数值都相等
2、基本导数公式

1. 常数函数的导数 ( 𝐶 ) ′ = 0 (𝐶)^′ = 0 (C)′=0
2. 幂函数的导数 ( x α ) ′ = α x α − 1 (x^α)^′ = αx^{α−1} (xα)′=αxα−1
3. 指数函数的导数 ( e x ) ′ = e x , ( a x ) ′ = a x l n a (e^x)^′ = e^x, (a^x)^′ = a^xlna (ex)′=ex,(ax)′=axlna
4. 对数函数的导数 ( l n x ) ′ = 1 x , ( l o g a x ) ′ = 1 x l n a (lnx)^′ = \dfrac{1}{x} , (log_ax)^′ = \dfrac{1}{xlna} (lnx)′=x1​,(loga​x)′=xlna1​
5. 三角函数的导数
   ( s i n x ) ′ = c o s x , ( c o s x ) ′ = − s i n x (sinx)^′ = cosx,(cosx)^′ = −sinx (sinx)′=cosx,(cosx)′=−sinx
   ( t a n x ) ′ = s e c 2 x , ( c o t x ) ′ = − c s c 2 x (tanx)^′ = sec^2x,(cotx)^′ = −csc^2x (tanx)′=sec2x,(cotx)′=−csc2x
   ( s e c x ) ′ = s e c x t a n x , ( c s c x ) ′ = − c s c x c o t x (secx)^′ = secxtanx,(cscx)^′ = −cscxcotx (secx)′=secxtanx,(cscx)′=−cscxcotx
   记忆口诀：常为 0，幂降次，s 变 c，c 反 s；指不变，对倒数
6. 反三角函数的导数
   ( a r c s i n x ) ′ = 1 1 − x 2 (arcsinx)^′ = \dfrac{1}{\sqrt{1-x^2}} (arcsinx)′=1−x2 ​1​
   ( a r c c o s x ) ′ = − 1 1 − x 2 (arccosx)^′ = − \dfrac{1}{\sqrt{1-x^2}} (arccosx)′=−1−x2 ​1​
   ( a r c t a n x ) ′ = 1 1 + x 2 (arctanx)^′ = \dfrac{1}{1+x^2} (arctanx)′=1+x21​
   ( a r c c o t x ) ′ = − 1 1 + x 2 (arccotx)^′ = − \dfrac{1}{1+x^2} (arccotx)′=−1+x21​
   3、函数在一点处可到与连续的关系
   函数在一点可导是比它在这一点处连续更强的一种性质
   定理：若函数$f(x)$在 x 0 x_0 x0​处可导，则$f(x)$在 x 0 x_0 x0​处连续. .
   注意：连续仅仅是可导的必要条件，而不是充分条件.
   例如，函数$f(x)=|x|$在$x=0$ 处连续，但由于，
   f − ′ ( 0 ) = lim ⁡ x → 0 − − x − 0 x = − 1 f^′_- (0) = { \lim\limits_{x \to 0^-}\dfrac{-x-0}{x}}= −1 f−′​(0)=x→0−lim​x−x−0​=−1
   f − ′ + ( 0 ) = lim ⁡ x → 0 + x − 0 x = 1 f^′_-+ (0) = { \lim\limits_{x \to 0^+}\dfrac{x-0}{x}}= 1 f−′​+(0)=x→0+lim​xx−0​=1
   所以$f(x)=|x|$在$x=0$处不可导.

微分

1、微分的概念

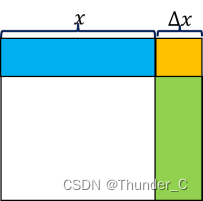
如图，边长为𝑥的正方形，当其边长增加了∆𝑥时，它的面积增加了
∆ S = ( x + ∆ x ) 2 − x 2 = 2 x ∆ x + ( ∆ x ) 2 ∆S = (x + ∆x)^2 − x^2 = 2x∆x + (∆x)^2 ∆S=(x+∆x)2−x2=2x∆x+(∆x)2.

上述面积的增加值由两部分构成， 2x∆x是∆x的一次项， ( ∆ x ) 2 (∆x)^2 (∆x)2满足
lim ⁡ ∆ x → 0 ( ∆ x ) 2 ∆ x = 0 {\lim\limits_{∆x \to 0} \dfrac{ (∆x)^2}{∆x}}=0 ∆x→0lim​∆x(∆x)2​=0,即 ( ∆ x ) 2 = o ( ∆ x ) . (∆x)^2 = o(∆x). (∆x)2=o(∆x).
2、函数在一点处的微分
定义：设函数$y=f(x)$在 𝑥 0 𝑥_0 x0​及其附近有定义，如果函数值$f(x)$在点 𝑥 0 𝑥_0 x0​处的改变量 ∆ 𝑓 ( 𝑥 0 ) ∆𝑓(𝑥_0) ∆f(x0​)可以表示成自变量改变量的一次项 𝑎 ( 𝑥 0 ) ∆ 𝑥 𝑎(𝑥_0)∆𝑥 a(x0​)∆x与自变量改变量的高阶无穷小量$o(∆x)$之和，即 ∆ f ( x 0 ) = a ( x 0 ) ∆ x + o ( ∆ x ) ∆f(x_0) = a(x_0)∆x + o(∆x) ∆f(x0​)=a(x0​)∆x+o(∆x)，则称函数$f(x)$在 x 0 x_0 x0​处可微， a ( x 0 ) ∆ x a(x_0)∆x a(x0​)∆x称为$f(x)$在 x 0 x_0 x0​处的微分，记作 d f ( x 0 ) = a ( x 0 ) ∆ x df(x_0) = a(x_0)∆x df(x0​)=a(x0​)∆x.
3、函数在一点处可微与可导的关系
微分计算公式
定理：函数$f(x)$在 x 0 x_0 x0​处可微的充要条件是函数$f(x)$在 x 0 x_0 x0​处可导，且 d f ( x 0 ) = f ′ ( x 0 ) d x df(x_0) = f^′(x_0)dx df(x0​)=f′(x0​)dx，其中$dx=∆x$.
本定理说明，一元函数的可导性与可微性是等价的性质，且导数值与微分值满足等式 f ′ ( x ) = d f ( x ) d x f^′(x) = \dfrac{df(x)}{dx} f′(x)=dxdf(x)​，即导数值等于函数微分与自变量微分的商，所以导数有时也称为微商.

导数的运算

1、导数的四则运算
定理：若函数$f(x),g(x)$在 𝑥 0 𝑥_0 x0​处可导，则其和、差、积、商构成的函数均在 𝑥 0 𝑥_0 x0​处可导，且：
⑴ [ 𝐟 ( 𝐱 ) ± 𝐠 ( 𝐱 ) ] ′ ∣ 𝐱 0 = 𝐟 ′ ( 𝐱 0 ) ± 𝐠 ′ ( 𝐱 0 ) [𝐟(𝐱) ± 𝐠(𝐱)]^′ |_{𝐱_0} = 𝐟^′(𝐱_0) ± 𝐠^′(𝐱_0) [f(x)±g(x)]′∣x0​​=f′(x0​)±g′(x0​)
⑵ [ 𝐟 ( 𝐱 ) 𝐠 ( 𝐱 ) ] ′ ∣ 𝐱 0 = 𝐟 ′ ( 𝐱 0 ) 𝐠 ( 𝐱 𝟎 ) + 𝐟 ( 𝐱 0 ) 𝐠 ′ ( 𝐱 0 ) [𝐟(𝐱)𝐠(𝐱)]^′ |_{𝐱_0} = 𝐟^′(𝐱_0)𝐠(𝐱_𝟎) + 𝐟(𝐱_0)𝐠^′(𝐱_0) [f(x)g(x)]′∣x0​​=f′(x0​)g(x0​)+f(x0​)g′(x0​)
⑶ [ 𝐟 ( 𝐱 ) 𝐠 ( 𝐱 ) ] ′ ∣ 𝐱 0 = 𝐟 ′ ( 𝐱 0 ) 𝐠 ( 𝐱 0 ) − 𝐟 ( 𝐱 0 ) 𝐠 ′ ( 𝐱 0 ) 𝐠 2 ( 𝐱 0 ) ( 𝐠 ( 𝐱 0 ) ≠ 0 ) [\dfrac{𝐟(𝐱)}{𝐠(𝐱)}]^′ |_{𝐱_0} = \dfrac{𝐟^′(𝐱_0)𝐠(𝐱_0)−𝐟(𝐱_0)𝐠^′(𝐱_0)}{𝐠^2(𝐱_0)} (𝐠(𝐱_0) \neq 0) [g(x)f(x)​]′∣x0​​=g2(x0​)f′(x0​)g(x0​)−f(x0​)g′(x0​)​(g(x0​)=0)
2、复合函数的链式求导法则
1.复合函数的链式求导法则
定理：设函数$y=f(g(x))$是函数$y=f(u)$和$u=g(x)$的复合，若$g(x)$在 x 0 x_0 x0​处可导，$f(u)$在 u 0 = g ( x 0 ) u_0 = g(x_0) u0​=g(x0​)处可导，则函数$y=f(g(x))$关于$x$在 x 0 x_0 x0​处的导数为：
d y d x ∣ x = x 0 = f ′ ( u 0 ) g ′ ( x 0 ) = f ′ ( g ( x 0 ) ) g ′ ( x 0 ) \dfrac{dy}{dx}|_{x=x_0} = f^′(u_0)g^′(x_0) = f^′(g(x_0))g^′(x_0) dxdy​∣x=x0​​=f′(u0​)g′(x0​)=f′(g(x0​))g′(x0​)
2.复合函数的微分
已知函数$y=f(u)$可微，利用微分计算公式，得 d y = f ′ ( u ) d u dy = f^′(u)du dy=f′(u)du，若函数$u=g(x)$可微，且复合函数$f(g(x))$有意义，则根据复合函数的链式求导法则及微分计算公式，可知$y=f(g(x))$的微分是
d y = d y d x d x = f ′ ( g ( x ) ) g ′ ( x ) d x = f ′ ( u ) d u = f ′ ( u ) u ′ ( x ) d x dy =\dfrac{dy}{dx}dx= f^′(g(x))g^′(x)dx = f^′(u)du = f^′(u)u^′(x)dx dy=dxdy​dx=f′(g(x))g′(x)dx=f′(u)du=f′(u)u′(x)dx
3、隐函数求导法
用自变量的解析式明显表达出来的函数叫显函数。
由方程$F(x,y)=0$确定𝑦是𝑥的函数且不能由显式给出的函数叫隐函数。
由方程$F(x,y)=0$确定的隐函数$y=y(x)$，将$y=y(x)$代入方程得恒等式
$F(x,y(x))=0$
隐函数存在且可导，利用复合函数求导法，上式两边同时对𝑥求导，求导时把𝑦看作中间变量，解出 𝑦 x ′ 𝑦^′_x yx′​的表达式（可含𝑦 ）。
4、对数求导法
1.当函数可以表示成多个因子的积、商，即 y = ∏ k = 1 m f k ( x ) ∏ k = 1 n g k ( x ) y=\dfrac{ ∏^m_{k=1}f_k(x)}{ ∏^n_{k=1}g_k(x)} y=∏k=1n​gk​(x)∏k=1m​fk​(x)​时，为了简化求导运算，可以在等式两端取
对数，将原式变成如下形式
l n y = ∑ k = 1 m l n f k ( x ) − ∑ k = 1 n l n g k ( x ) lny = ∑^m_{k=1}lnf_k(x) − ∑^n_{k=1}lng_k(x) lny=∑k=1m​lnfk​(x)−∑k=1n​lngk​(x) ，
2.在求函数 y = 𝑓 ( 𝑥 ) 𝑔 ( 𝑥 ) y = 𝑓(𝑥)^{𝑔(𝑥)} y=f(x)g(x)的导数时，可以在等式两端取对数，将原式变成如下形式：$lny=g(x)lnf(x)$，两端关于变量 $x$ 求导，将 $y$ 看作是中间变量，得
y ′ y = g ′ ( x ) l n f ( x ) + g ( x ) f ( x ) f ′ ( x ) \dfrac{y^′}{y} = g^′(x)lnf(x) + \dfrac{g(x)}{f(x)}f^′(x) yy′​=g′(x)lnf(x)+f(x)g(x)​f′(x)
所以 y ′ = f ( x ) g ( x ) [ g ′ ( x ) l n f ( x ) + g ( x ) f ( x ) f ′ ( x ) ] y^′ = f(x)^{g(x)} [g^′(x)lnf(x) + \dfrac{g(x)}{f(x)}f^′(x)] y′=f(x)g(x)[g′(x)lnf(x)+f(x)g(x)​f′(x)]
5、高阶导数
当运动物体移动的距离 $S$ 与移动时间 $t$ 之间的关系式$S=S(t)$已知时，导数 𝑆 ′ ( 𝑡 ) 𝑆^′(𝑡) S′(t)表示的是该物体在 $t$ 时刻的瞬时速度$v(t)$，即 𝑣 ( 𝑡 ) = 𝑆 ′ ( 𝑡 ) 𝑣(𝑡) = 𝑆^′(𝑡) v(t)=S′(t)。该物体在 $t$ 时刻的加速度$a(t)$指的是
lim ⁡ ∆ t → 0 ( v ( t + ∆ t ) − v ( t ) ∆ t = v ′ ( 𝑡 ) {\lim\limits_{∆t \to 0} \dfrac{ (v(t+∆t)-v(t)}{∆t}}=v^′(𝑡) ∆t→0lim​∆t(v(t+∆t)−v(t)​=v′(t)
即$a(t)$是$s(t)$的导数的导数。为了明确$a(t)$与$s(t)$的关系，需要引进二阶导数的概念.
设函数$f(x)$在$(a,b)$内有定义，并在$(a,b)$中的每一点$x$都有导数 𝑓 ′ ( 𝑥 ) 𝑓^′(𝑥) f′(x)，这种对应就定义了一个新的函数关系，称这个函数为$f(x)$ 在$(a,b)$内的导函数，记为 y = 𝑓 ′ ( 𝑥 ) . y = 𝑓^′(𝑥). y=f′(x).
如果导函数 f ′ ( x ) f^′(x) f′(x)还是一个$(a,b)$内的可导函数，那么它的导数 [ f ′ ( x ) ] ′ [f^′(x)]^′ [f′(x)]′就称为函数$f(x)$的二阶导数，
记作 f ′′ ( x ) f^{′′}(x) f′′(x)，即 f ′′ ( x ) = [ f ′ ( x ) ] ′ f^{′′}(x) = [f^′(x)]^′ f′′(x)=[f′(x)]′.
函数𝑓(𝑥)的三阶导数定义为 f ′′′ ( x ) = [ f ′′ ( x ) ] ′ f^{′′′}(x) = [f^{′′}(x)]^′ f′′′(x)=[f′′(x)]′.
二阶和高于二阶的导数统称为高阶导数。函数$f(x)$的$n$ 阶导数记作 f ( n ) ( x ) f^{(n)}(x) f(n)(x)或 d n f ( x ) f x n \dfrac{d^nf(x)}{fx^n} fxndnf(x)​，其定义为
f ( n ) ( x ) = [ f n − 1 ( x ) ] ′ f^{(n)}(x) = [f^{n-1}(x)]^′ f(n)(x)=[fn−1(x)]′或 d n f ( x ) d x n = d d x [ d n − 1 f ( x ) d x n − 1 ] \dfrac{d^nf(x)}{dx^n} = \dfrac{d}{dx}[\dfrac{d^{n-1}f(x)}{dx^{n-1}}] dxndnf(x)​=dxd​[dxn−1dn−1f(x)​]

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！