Matlab 使用最小二乘法拟合球面（待验证）

功能

根据给出点的笛卡尔坐标，使用最小二乘法拟合球面并且返回球的球心坐标及半径。要求给出有效点的数目不少于4。

实现思路

在matlab中有相应的函数实现，苦于理解实现详细。于是使用基础的方式来实现这个功能。

步骤

1. 得到残差和公式
   $$F = \sum_{i=1}^n [(x_i-a)^2+(y_i-b)^2+(z_i-c)^2-R^2]^2$$

2. 分别将残差和对参数求偏导
   

   $$\frac{\partial F}{\partial a} = -4\sum_{i=1}^n(x_i-a)[(x_i-a)^2+(y_i-b)^2+(z_i-c)^2-R^2]$$
   $$\frac{\partial F}{\partial b} = -4\sum_{i=1}^n(y_i-b)[(x_i-a)^2+(y_i-b)^2+(z_i-c)^2-R^2]$$
   $$\frac{\partial F}{\partial c} = -4\sum_{i=1}^n(z_i-c)[(x_i-a)^2+(y_i-b)^2+(z_i-c)^2-R^2]$$
   $$\frac{\partial F}{\partial R} = -4R\sum_{i=1}^n[(x_i-a)^2+(y_i-b)^2+(z_i-c)^2-R^2]$$

3. 将点坐标值带入各个残差和偏导，令值为0，构造方程组
   

   $$\begin{cases} \frac{\partial F}{\partial a} = 0 \\[2ex] \frac{\partial F}{\partial b} = 0 \\[2ex] \frac{\partial F}{\partial c} = 0 \\[2ex] \frac{\partial F}{\partial R} = 0 \end{cases}$$

4. 求解偏导方程组

5. 选取有效值

命令概要

sym     % 构造符号数字，变量或者对象
syms    % 构造符号变量
diff    % 微分或求偏导
subs    % 符号替换
solve   % 解代数方程组

实现

function [a,b,c,R] = fitspherebyls(xyz)
%% use Least-Squares to fit sphere
% xyz
% x1 y1 z1
% x2 y2 z2
% x3 y3 z3
% x4 y4 z4% 去除重复点data = unique(xyz,'rows');row = size(data,1);if row<4warning('points too less');a = [];b = [];c = [];R = [];return;endsyms x y z a b c R;F = sym(((x-a)^2+ (y-b)^2+ (z-c)^2-R^2)^2);Fda = diff(F,'a');Fdb = diff(F,'b');Fdc = diff(F,'c');FdR = diff(F,'R');Q1 = sym(0);Q2 = sym(0);Q3 = sym(0);Q4 = sym(0);for i = 1:rowQ1 = Q1+subs(Fda,{x,y,z},{data(i,:)});Q2 = Q2+subs(Fdb,{x,y,z},{data(i,:)});Q3 = Q3+subs(Fdc,{x,y,z},{data(i,:)});Q4 = Q4+subs(FdR,{x,y,z},{data(i,:)});end
% maybe accelerate the next step's solving
%     Q1 = simplify(Q1);
%     Q2 = simplify(Q2);
%     Q3 = simplify(Q3);
%     Q4 = simplify(Q4);[a,b,c,R] = solve([Q1,Q2,Q3,Q4],[a,b,c,R]);% get valid resolver indexexactindex = find(R>0);if length(exactindex)~=1warning('there exists several solvers!');enda = a(exactindex);b = b(exactindex);c = c(exactindex);R = R(exactindex);a = double(a);b = double(b);c = double(c);R = double(R);
end

结果

% 测试
[a,b,c,R] = fitspherebyls(xyz);
figure;
drawsphere(a,b,c,R);
hold on;
plot3(xyz(:,1),xyz(:,2),xyz(:,3),'go');

注：drawsphere

% 数据
xyz = [0.000048179270400   0.000974212773000   0.000973191636000;0.000025318593500   0.000999572338000                   0;0.000101367950000   0.002008911220000                   0;0.000000000000000   0.000000000000000   0.000000000000000;0.000025352224800  -0.000000000000000   0.000999571173000;0.000048179270400  -0.000974212773000   0.000973191636000;0.000025318593500  -0.000999572338000                   0;0.000101501493000  -0.000000000000000   0.002008893060000]
% 结果
a = 0.020001153020509
b = 3.341785572735592e-07
c =-3.010937940913924e-06
R = 0.020000863489075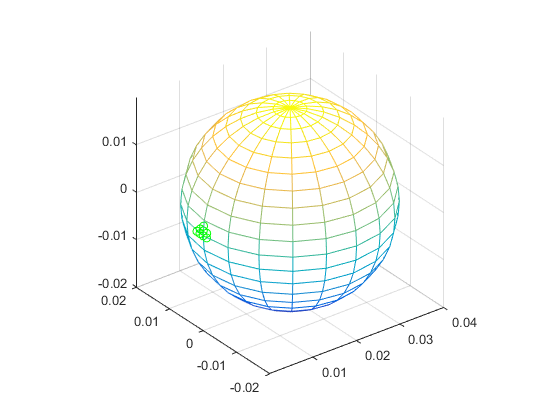

% 数据
xyz = [0.033740036200000   0.024673352000000   0.000000000002491;0.039257969700000   0.026234770200000   0.000000000008931;0.039007559400000   0.026130110000000   0.000967862085000;0.033495158000000   0.024572286800000   0.000909697381000;0.048077128800000   0.028730340300000   0.000000000020469;0.047817859800000   0.028619924600000   0.001060877460000;0.025288350900000   0.022253016000000   0.000823148352000;0.025050554400000   0.022142505300000   0.001719459190000;0.033248167500000   0.024454629000000   0.001899488150000;0.038754388700000   0.026007646700000   0.002020468700000]
% 结果
a =-0.368054174150326
b = 1.455102906016445
c = 0.058582848220979
R = 1.486959475326920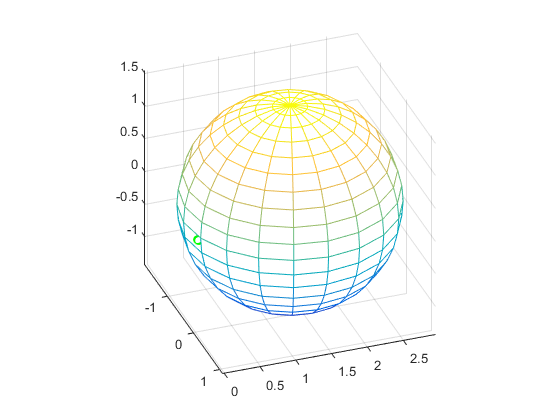

注：绿色为输入的点数据。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！