模拟CMOS集成电路设计入门学习（14）

有源电流镜

（1）小信号增益

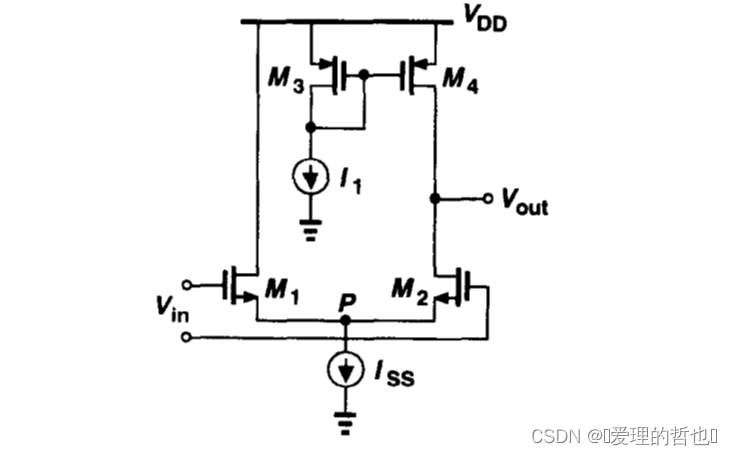
 分析上图所示差动放大器的小信号增益

方法一：

因为，由下图可得：

 我们只需再计算出即可。

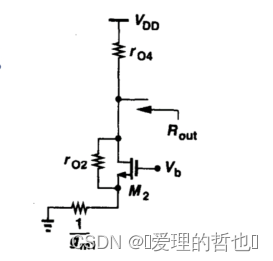
 M2受到M1的源级输出阻抗的负反馈，因此等效的输出阻抗等于，

{公式：源端带负载，从漏端看进去的等效输出阻抗=，这里忽略了体效应}

从而·，

所以

{如果，则}

方法二：

先分别计算出和，并将结果相乘得到。

①计算

借助上图，我们可以求出：

其中表示从M2源端看进去得到的电阻。因为M2的漏端接有一个相对大的电阻. 

 的值必须借助公式（3.110）得到：

{ 公式（3.110）表明,当在源端看输入阻抗时,漏端的阻抗要除以}

由此可得出：

{如果,；如果，。}

②计算

 可得：

③计算

 （2）大信号特性

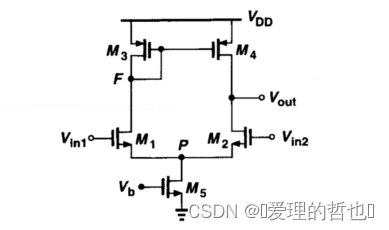
①如果相对于足够的负，M1、M3、M4均关断。因为没有电流可以从流出，M2和M5都工作在深线性区，传输的电流为0。因此，；

②随着接近,M1导通，使的部分电流流过M3，且使M4开启。

从而输出电压就依赖于和之间的差值；

③和很接近时，M2和M4都处于饱和区，产生一个很高的增益；

④当变得比正得多的时候，，，增大而减小，最终驱使进入线性区；

⑤如果足够大，M2关断，M4的电流为0且工作在深线性区，从而

 同时，在实际上，电路中的不对称可能会导致产生一个大的偏差，很可能驱使M2或者M4进入线性区。例如，如果M2的阈值电压稍小于M1的阈值电压，即使，前者的电流也比后者大，使显著下降。因此，该电路很少在开环的情况下用来放大小信号。

（3）小信号分析

（4）共模特性

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！