高斯列主元消去法求解方程组，附c++代码与使用java实现代码

，1，列主元消去法思想

   在顺序消元法中，ann是被除数，所以ann不能为0，另外，若ann很小，计算结果可能引入较大误差。因此，在进行第K次（k>=1）变换前，在[k，n]行之间找到主元素最大的那一行，和第K行交换位置，这样保证akk始终是该列中绝对值最大的那一个。然后在接着使用高斯顺序消元法进行求解即可。

2，代码实现

   在原本顺序消元法的基础上，定义了maxValue列主元最大值，和maxRow列主元最大行，此行也就是需要交换的行。先通过for循环找出列中最大值所在的行，并将该行所在的数组下标，赋值给maxRow。然后在通过一次for循环将当前所在的第K行与找到的最大行进行交换，通过定义一个中间变量temp来将存储两行元素数组中的值进行交换，然后在进行高斯顺序消元法即可。

3，c++代码

      这里c++代码，矩阵数据的输入和输出使用的是txt文件输入输出，具体的txt数据格式请看上一篇关于顺序消元法的代码，C++顺序消元法

#include 
#include  
#include  
#include using namespace std;int main(){int i,j,k,n;double eps,ratio,sum;ifstream data_in("gauss_source.txt");ofstream data_out("gauss_result.txt");//输入增广矩阵系数data_in>>n; //输入方程个数double *x=new double[n]; //动态分配存储空间（指针）double **a =new double*[n]; //二级指针指向指针数组首地址，n 个方程，二维动态数组for(i=0; i>a[i][j]; //输入系数矩阵}}for(i=0; i>a[i][n]; //输入等号右端向量的各元素 a[][]为增广矩阵}data_in>>eps; //输入最小主元素.为了避免主元素为 0 的情况，设置一个比较小的实数data_in.close();//***********************列主元消去法*******************************double maxValue;//列主元最大值int maxRow;//列主元最大行，也就是需要交换的行for(k=0; k<(n-1); k++) {//先找到列主元的最大行maxRow=k;maxValue=abs(a[k][k]);int m;for(m=k+1;mmaxValue){maxRow=m;maxValue=abs(a[m][k]);}}//交换第k行与第maxrow行//遍历每一个元素for(m=k;m<=n;m++){double temp=a[k][m];a[k][m]=a[maxRow][m];a[maxRow][m]=temp;}//*******************接下来是高斯顺序消元法*************************for(i=(k+1); i=0; --i){sum=0.0;for(j=(i+1); j
 
输出：
 
 
再附上自己使用java代码重新实现的顺序消元法的结果，这次采用的是键盘输入的方式，输入数据。
 
import java.util.Scanner;
import static java.lang.Math.abs;/*** @program: new begin new study* @description: 列主元消元法* @author: FMm* @create: 2022-03-27 20:51**/
public class guass_soltuion {public static void main(String[] args) {int n;//方程未知数的个数double eps;//eps最小住院Scanner sc = new Scanner(System.in);System.out.print("请输入方程的个数：");n = sc.nextInt();double[] arr = new double[n];double[][] arr2 = new double[n][n + 1];for (int i = 0; i < n; i++) {//输入矩阵系数与bfor (int j = 0; j <= n; j++) {if (j != n) {System.out.println("请输入第"+(i+1)+"行X"+ j);} else {System.out.println("请输入第"+(i+1)+"行b"+ i);}arr2[i][j] = sc.nextDouble();}}System.out.println("请输入eps");eps=sc.nextDouble();guass_sequence(arr2,arr,eps,n);guass_output(n,arr);}/*** @author: FMm* @description: 用通过列主元消去法求上三角矩阵，并回代求值* @param: arr2temp 增广矩阵数组* @param: arr 用来回代存放xi值得数组* @param: eps * @param: n x的个数* @return: void* @create: 2022/3/29 15:25*/public static void guass_sequence (double[][] arr2temp,double[] arr,double eps,int n){double maxValue;//列主元最大值int maxRow;//列主元最大行，也就是需要交换的行double ratio;double sum;for(int k=0;kmaxValue){maxRow=m;maxValue=abs(arr2temp[m][k]);}}//交换第k行与第maxrow行//遍历每一个元素for(m=k;m<=n;m++){double temp=arr2temp[k][m];arr2temp[k][m]=arr2temp[maxRow][m];arr2temp[maxRow][m]=temp;}for(int i=(k+1); i=0; --i){sum=0.0;for(int j=(i+1); j
 
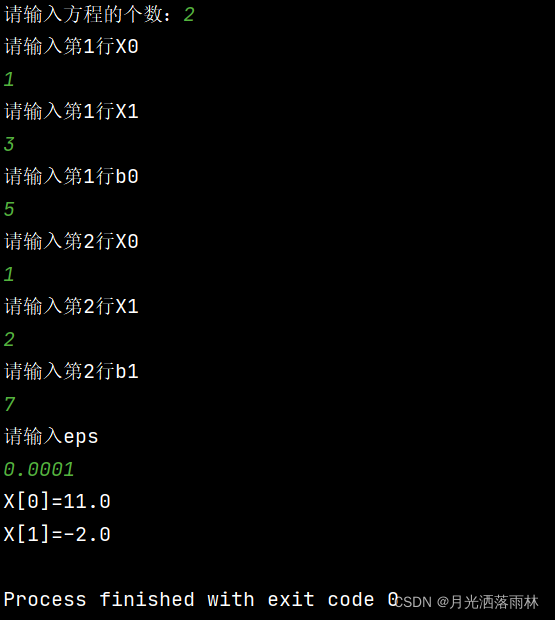
 输入及输出结果：
 
 
 
                        

                        

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！