学习笔记--电磁场与电磁波（1）

电磁场与电磁波

文章目录

• 电磁场与电磁波
• 1 数学基础
• • 1.1 矢量分析
  • • 1.1.1 基本定义
    • 1.1.2 矢量基本运算
  • 1.2 场的分析
  • • 1.2.1 场的分析方法（即函数的分析方法）
    • 1.2.2 场的宏观分析
    • • 标量场（函数）的等值面
      • 矢量场的矢量线
    • 1.2.3 场的微观分析
    • • 标量场（函数）的方向导数和梯度
      • 梯度运算法则
      • 梯度计算
      • 矢量场（函数）的通量和散度
      • 矢量场（函数）的环量和旋度
      • 两个重要恒等式
  • 1.4 亥姆霍兹定理
  • 1.5 三种坐标系
  • • 1.5.1 直角坐标系
    • 1.5.2 柱坐标系
    • 1.5.3 球坐标系

1 数学基础

1.1 矢量分析

1.1.1 基本定义

• 矢量：既有大小又有方向的量；

• 标量：只有大小没有方向的量；

• 矢量函数：一元矢量函数的定义，给定自变量 $t$ ，定义域为$[a,b]$ ，有一种对应关系 A ⃗ = A ⃗ ( t ) \vec{A}=\vec{A}(t) A =A (t)，则称 A ⃗ \vec{A} A 是 $t$ 的一元矢量函数。

• 时空矢量函数：在直角坐标系下，以空间和时间为自变量的四元矢量函数可以表示为：
  A ⃗ = A ⃗ ( x , y , z , t ) = A x ( x , y , z , t ) e ⃗ x + A y ( x , y , z , t ) e ⃗ y + A z ( x , y , z , t ) e ⃗ z = A x e ⃗ x + A y e ⃗ y + A z e ⃗ z \begin{align} \vec{A} &= \vec{A}(x,y,z,t) \\ &= A_x(x,y,z,t)\vec{e}_x + A_y(x,y,z,t)\vec{e}_y + A_z(x,y,z,t)\vec{e}_z \\& =A_x\vec{e}_x + A_y\vec{e}_y + A_z\vec{e}_z \end{align} A ​=A (x,y,z,t)=Ax​(x,y,z,t)e x​+Ay​(x,y,z,t)e y​+Az​(x,y,z,t)e z​=Ax​e x​+Ay​e y​+Az​e z​​​

1.1.2 矢量基本运算

• 矢量加法：
  A ⃗ + B ⃗ = ( A x e ⃗ x + A y e ⃗ y + A z e ⃗ z ) + ( B x e ⃗ x + B y e ⃗ y + B z e ⃗ z ) = ( A x + B x ) e ⃗ x + ( A y + B y ) e ⃗ y + ( A z + B z ) e ⃗ z \begin{align} \vec{A} +\vec{B} &= (A_x\vec{e}_x + A_y\vec{e}_y + A_z\vec{e}_z) + (B_x\vec{e}_x + B_y\vec{e}_y + B_z\vec{e}_z) \\& = (A_x+B_x)\vec{e}_x + (A_y+B_y)\vec{e}_y + (A_z+B_z)\vec{e}_z \end{align} A +B ​=(Ax​e x​+Ay​e y​+Az​e z​)+(Bx​e x​+By​e y​+Bz​e z​)=(Ax​+Bx​)e x​+(Ay​+By​)e y​+(Az​+Bz​)e z​​​

• 矢量减法：
  A ⃗ − B ⃗ = ( A x e ⃗ x + A y e ⃗ y + A z e ⃗ z ) − ( B x e ⃗ x + B y e ⃗ y + B z e ⃗ z ) = ( A x − B x ) e ⃗ x + ( A y − B y ) e ⃗ y + ( A z − B z ) e ⃗ z \begin{align} \vec{A} - \vec{B} &= (A_x\vec{e}_x + A_y\vec{e}_y + A_z\vec{e}_z) - (B_x\vec{e}_x + B_y\vec{e}_y + B_z\vec{e}_z) \\& = (A_x-B_x)\vec{e}_x + (A_y-B_y)\vec{e}_y + (A_z-B_z)\vec{e}_z \end{align} A −B ​=(Ax​e x​+Ay​e y​+Az​e z​)−(Bx​e x​+By​e y​+Bz​e z​)=(Ax​−Bx​)e x​+(Ay​−By​)e y​+(Az​−Bz​)e z​​​

• 矢量点乘：
  A ⃗ ⋅ B ⃗ = B ⃗ ⋅ A ⃗ = ( A x e ⃗ x + A y e ⃗ y + A z e ⃗ z ) ⋅ ( B x e ⃗ x + B y e ⃗ y + B z e ⃗ z ) = ( A x B x ) + ( A y B y ) + ( A z B z ) = ∣ A ⃗ ∣ ∣ B ⃗ ∣ cos ⁡ θ \begin{align} \vec{A} \cdot \vec{B} &= \vec{B} \cdot \vec{A} \\&= (A_x\vec{e}_x + A_y\vec{e}_y + A_z\vec{e}_z) \cdot (B_x\vec{e}_x + B_y\vec{e}_y + B_z\vec{e}_z) \\& = (A_x B_x) + (A_y B_y) + (A_z B_z) \\& = |\vec{A}| |\vec{B}|\cos \theta \end{align} A ⋅B ​=B ⋅A =(Ax​e x​+Ay​e y​+Az​e z​)⋅(Bx​e x​+By​e y​+Bz​e z​)=(Ax​Bx​)+(Ay​By​)+(Az​Bz​)=∣A ∣∣B ∣cosθ​​

• 矢量叉乘：
  A ⃗ × B ⃗ = − B ⃗ × A ⃗ = ( A x e ⃗ x + A y e ⃗ y + A z e ⃗ z ) × ( B x e ⃗ x + B y e ⃗ y + B z e ⃗ z ) = ∣ e ⃗ x e ⃗ y e ⃗ z A x A y A z B x B y B z ∣ = ( A y B z − A z B y ) e ⃗ x + ( A z B x − A x B z ) e ⃗ y + ( A x B y − A y B x ) e ⃗ z = n ⃗ ∣ A ⃗ ∣ ∣ B ⃗ ∣ sin ⁡ θ \begin{align} \vec{A} \times \vec{B} &= - \vec{B} \times \vec{A} \\&= (A_x\vec{e}_x + A_y\vec{e}_y + A_z\vec{e}_z) \times (B_x\vec{e}_x + B_y\vec{e}_y + B_z\vec{e}_z) \\ \\& = \begin{vmatrix} \vec{e}_x & \vec{e}_y & \vec{e}_z\\ A_x & A_y & A_z\\ B_x & B_y & B_z\\ \end{vmatrix} \\ \\& = (A_y B_z - A_z B_y)\vec{e}_x + (A_z B_x - A_x B_z)\vec{e}_y + (A_x B_y - A_y B_x)\vec{e}_z \\& = \vec{n} |\vec{A}| |\vec{B}|\sin \theta \end{align} A ×B ​=−B ×A =(Ax​e x​+Ay​e y​+Az​e z​)×(Bx​e x​+By​e y​+Bz​e z​)= ​e x​Ax​Bx​​e y​Ay​By​​e z​Az​Bz​​ ​=(Ay​Bz​−Az​By​)e x​+(Az​Bx​−Ax​Bz​)e y​+(Ax​By​−Ay​Bx​)e z​=n ∣A ∣∣B ∣sinθ​​
  n ⃗ \vec{n} n 的方向符合右手定则。

• 矢量混合积：
  A ⃗ × B ⃗ ⋅ C ⃗ = ( A ⃗ × B ⃗ ) ⋅ C ⃗ \begin{align} \vec{A} \times \vec{B} \cdot \vec{C} &= (\vec{A} \times \vec{B}) \cdot \vec{C} \end{align} A ×B ⋅C ​=(A ×B )⋅C ​​
  先算叉乘再算点乘，计算结果为标量；

  重要矢量恒等式：

A ⃗ × B ⃗ ⋅ C ⃗ = B ⃗ × C ⃗ ⋅ A ⃗ = C ⃗ × A ⃗ ⋅ B ⃗ C ⃗ ⋅ A ⃗ × B ⃗ = A ⃗ ⋅ B ⃗ × C ⃗ = B ⃗ ⋅ C ⃗ × A ⃗ \begin{align} \vec{A} \times \vec{B} \cdot \vec{C} &= \vec{B} \times \vec{C} \cdot \vec{A} = \vec{C} \times \vec{A} \cdot \vec{B} \\ \vec{C} \cdot \vec{A} \times \vec{B} &= \vec{A} \cdot \vec{B} \times \vec{C} = \vec{B} \cdot \vec{C} \times \vec{A} \end{align} A ×B ⋅C C ⋅A ×B ​=B ×C ⋅A =C ×A ⋅B =A ⋅B ×C =B ⋅C ×A ​​

1.2 场的分析

1.2.1 场的分析方法（即函数的分析方法）

1.2.2 场的宏观分析

标量场（函数）的等值面

定义：标量场仅有大小，具有相同函数值的点的集合，这些点组成一个曲面，该曲面称为等值面。

表示方式： A = A ( x , y , z , t 0 ) = C A=A(x,y,z,t_0)=C A=A(x,y,z,t0​)=C，$C$为常数；

矢量场的矢量线

定义：矢量场既有大小又有方向，一般用一些有向线来形象地表示它的空间分布，这些有向线称为矢量线。

表示方式： A ⃗ = A x e ⃗ x + A y e ⃗ y + A z e ⃗ z \vec{A}=A_x\vec{e}_x+A_y\vec{e}_y+A_z\vec{e}_z A =Ax​e x​+Ay​e y​+Az​e z​

1.2.3 场的微观分析

标量场（函数）的方向导数和梯度

（1）标量场（函数）的方向导数

定义：在函数定义域内的点，对某一方向求导得的导数；

数学描述：

设标量场函数
φ = 抽象 φ ( M ) = 直坐标 φ ( x , y , z ) \varphi \overset{\text{抽象}}{=} \varphi (M) \overset{\text{直坐标}}{=} \varphi (x,y,z) φ=抽象φ(M)=直坐标φ(x,y,z)
定义域内，考察任意一点 M 0 M_0 M0​，其邻域内，考察任意一点 $M$，前者向后者连线方向 l ⃗ \vec{l} l 构成某一方向，两点之间的距离是 $\rho$，则将
∂ φ ∂ l ∣ M 0 = lim ⁡ ρ → 0 φ ( M ) − φ ( M 0 ) ρ = lim ⁡ ρ → 0 φ ( x 0 + Δ x , y 0 + Δ y , z 0 + Δ z ) − φ ( x 0 , y 0 , z 0 ) ρ = lim ⁡ ρ → 0 因变量变化量 长度变化量 \begin{align} \frac{\partial \varphi}{\partial l}{|}_{M_0} &= \underset{\rho\to 0}{\lim} \frac{\varphi(M)-\varphi(M_0)}{\rho} \\&= \underset{\rho\to 0}{\lim} \frac{\varphi(x_0 + \Delta x,y_0 + \Delta y,z_0 + \Delta z) - \varphi(x_0,y_0,z_0)}{\rho} \\&= \underset{\rho\to 0}{\lim} \frac{因变量变化量}{长度变化量} \end{align} ∂l∂φ​∣M0​​​=ρ→0lim​ρφ(M)−φ(M0​)​=ρ→0lim​ρφ(x0​+Δx,y0​+Δy,z0​+Δz)−φ(x0​,y0​,z0​)​=ρ→0lim​长度变化量因变量变化量​​​
定义为函数 $\phi$ 在 M 0 M_0 M0​ 点沿 l ⃗ \vec{l} l 的方向导数。

直角坐标系下方向导数的计算：

若场（函数）$\phi =\phi (x,y,z)$ 在点 $M(x,y,z)$ 处可微，$\cos \alpha$、$\cos \beta$、$\cos \gamma$ 为方向 l ⃗ \vec{l} l 的方向余弦，则场在该点处沿该方向的方向导数必定存在，且为
∂ φ ∂ l ∣ M = ∂ φ ∂ x cos ⁡ α + ∂ φ ∂ y cos ⁡ β + ∂ φ ∂ z cos ⁡ γ \frac{\partial \varphi}{\partial l}{|}_{M}= \frac{\partial \varphi}{\partial x}\cos \alpha + \frac{\partial \varphi}{\partial y}\cos \beta + \frac{\partial \varphi}{\partial z}\cos \gamma ∂l∂φ​∣M​=∂x∂φ​cosα+∂y∂φ​cosβ+∂z∂φ​cosγ

（2）标量场（函数）的梯度

定义：梯度是一个矢量，表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

数学描述：
G ⃗ = g r a d φ = ∂ φ ∂ x e ⃗ x + ∂ φ ∂ y e ⃗ y + ∂ φ ∂ z e ⃗ z \begin{align} \vec{G} &= grad \, \varphi \\&= \frac{\partial \varphi}{\partial x}\vec{e}_x + \frac{\partial \varphi}{\partial y}\vec{e}_y + \frac{\partial \varphi}{\partial z}\vec{e}_z \end{align} G ​=gradφ=∂x∂φ​e x​+∂y∂φ​e y​+∂z∂φ​e z​​​

称为 $\phi$ 的梯度；

由于上述写法过于麻烦，引入哈密顿算符简化写法：
g r a d φ = ∂ φ ∂ x e ⃗ x + ∂ φ ∂ y e ⃗ y + ∂ φ ∂ z e ⃗ z = ( ∂ ∂ x e ⃗ x + ∂ ∂ y e ⃗ y + ∂ ∂ z e ⃗ z ) φ = ∇ φ ∇ = ∂ ∂ x e ⃗ x + ∂ ∂ y e ⃗ y + ∂ ∂ z e ⃗ z \begin{align} grad \, \varphi &= \frac{\partial \varphi}{\partial x}\vec{e}_x + \frac{\partial \varphi}{\partial y}\vec{e}_y + \frac{\partial \varphi}{\partial z}\vec{e}_z \\&= ( \frac{\partial}{\partial x}\vec{e}_x + \frac{\partial}{\partial y}\vec{e}_y + \frac{\partial}{\partial z}\vec{e}_z ) \, \varphi \\&= \nabla \varphi \\ \\ \nabla &= \frac{\partial}{\partial x}\vec{e}_x + \frac{\partial}{\partial y}\vec{e}_y + \frac{\partial}{\partial z}\vec{e}_z \end{align} gradφ∇​=∂x∂φ​e x​+∂y∂φ​e y​+∂z∂φ​e z​=(∂x∂​e x​+∂y∂​e y​+∂z∂​e z​)φ=∇φ=∂x∂​e x​+∂y∂​e y​+∂z∂​e z​​​

梯度运算法则

设 $c$ 为常数，$u$ 和 $v$ 为两个标量场（函数）
∇ c = 0 ∇ ( c u ) = c ∇ u ∇ ( u ± v ) = ∇ u ± ∇ v ∇ ( u v ) = v ∇ u + u ∇ v ∇ ( u v ) = 1 v 2 ( v ∇ u − u ∇ v ) ∇ [ f ( u ) ] = f ′ ( u ) ∇ u \begin{align} & \nabla c = 0 \\ & \nabla(cu) = c\nabla u \\ & \nabla(u\pm v) = \nabla u \pm \nabla v \\ & \nabla(u v) = v \nabla u + u \nabla v\\ & \nabla(\frac{u}{v}) = \frac{1}{v^2} (v \nabla u - u \nabla v)\\ & \nabla[f(u)] = f'(u)\nabla u \end{align} ​∇c=0∇(cu)=c∇u∇(u±v)=∇u±∇v∇(uv)=v∇u+u∇v∇(vu​)=v21​(v∇u−u∇v)∇[f(u)]=f′(u)∇u​​

梯度计算

直角坐标系下的点 $P(x,y,z)$ 与坐标原点确定的矢量为 r ⃗ \vec{r} r 与坐标原点之间的距离为 $r$，求 ∇ 1 r \nabla\frac{1}{r} ∇r1​、$\nabla r$。
∇ 1 r = − r ⃗ 0 r 2 = − r ⃗ r 3 ∇ r = r ⃗ 0 \nabla\frac{1}{r} = -\frac{\vec{r}_0}{r^2}=-\frac{\vec{r}}{r^3} \\ \nabla r = \vec{r}_0 ∇r1​=−r2r 0​​=−r3r ​∇r=r 0​

矢量场（函数）的通量和散度

以矢量场 A ⃗ = A ⃗ ( x , y , z , t ) \vec{A}=\vec{A}(x,y,z,t) A =A (x,y,z,t) 为例；

通量的定义：

• 开曲面矢量场的通量：
  ψ = ∫ s A ⃗ ⋅ d S ⃗ = ∫ s A ⃗ ⋅ n ⃗ d S \psi = \int_s\vec{A} \cdot d\vec{S} = \int_s\vec{A} \cdot \vec{n} d S ψ=∫s​A ⋅dS =∫s​A ⋅n dS

• 闭曲面矢量场的通量：
  ψ = ∮ s A ⃗ ⋅ d S ⃗ = ∮ s A ⃗ ⋅ n ⃗ d S \psi = \oint_s\vec{A} \cdot d\vec{S} = \oint_s\vec{A} \cdot \vec{n} d S ψ=∮s​A ⋅dS =∮s​A ⋅n dS

面方向的定义：

• 开曲面：满足右手螺旋的方向 n ⃗ \vec{n} n
• 闭曲面：朝外法线方向 n ⃗ \vec{n} n

通量的物理意义：

• 从定义式看出是点乘，结果是标量，仅有大小。按点乘几何意义的 A ⃗ \vec{A} A 要向 n ⃗ \vec{n} n 的方向投影，投影后就与面垂直。

• 对于封闭面，标量就要考虑大小的几种可能

  $\psi >0$：净通量流出，内部有源；

  $\psi <0$：净通量流入，内部有洞（负源）；

  $\psi =0$：无源。对应无源场；

散度的定义

单位体积的通量，即通量密度为散度；
d i v A ⃗ = lim ⁡ Δ V → 0 ∮ s A ⃗ ⋅ d S ⃗ Δ V = ∇ ⋅ A ⃗ = ( ∂ ∂ x e ⃗ x + ∂ ∂ y e ⃗ y + ∂ ∂ z e ⃗ z ) ⋅ ( A x e ⃗ x + A y e ⃗ y + A z e ⃗ z ) = ∂ A x ∂ x + ∂ A y ∂ y + ∂ A z ∂ z \begin{align} div\,\vec{A} &= \underset{\Delta V\to 0}{\lim} \frac{\oint_s\vec{A} \cdot d\vec{S}}{\Delta V} \\&= \nabla\cdot\vec{A} \\&= (\frac{\partial}{\partial x}\vec{e}_x + \frac{\partial}{\partial y}\vec{e}_y + \frac{\partial}{\partial z}\vec{e}_z) \cdot (A_x\vec{e}_x + A_y\vec{e}_y + A_z\vec{e}_z) \\&= \frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z} \end{align} divA ​=ΔV→0lim​ΔV∮s​A ⋅dS ​=∇⋅A =(∂x∂​e x​+∂y∂​e y​+∂z∂​e z​)⋅(Ax​e x​+Ay​e y​+Az​e z​)=∂x∂Ax​​+∂y∂Ay​​+∂z∂Az​​​​

散度定理（高斯公式）

计算式等于定义式。
∇ ⋅ A ⃗ = lim ⁡ Δ V → 0 ∮ s A ⃗ ⋅ d S ⃗ Δ V \begin{align} \nabla\cdot\vec{A} &= \underset{\Delta V\to 0}{\lim} \frac{\oint_s\vec{A} \cdot d\vec{S}}{\Delta V} \end{align} ∇⋅A ​=ΔV→0lim​ΔV∮s​A ⋅dS ​​​
右边的 $\Delta V$ 和极限符号移到左边，并对左边体积分得到
∫ V ∇ ⋅ A ⃗ d V = ∮ s A ⃗ ⋅ d S ⃗ \begin{align} \int_V \nabla \cdot \vec{A} \,dV &= {\oint_s\vec{A} \cdot d\vec{S}} \end{align} ∫V​∇⋅A dV​=∮s​A ⋅dS ​​
提示：

• 积分方程组和微分方程组的互化纽带；
• 右边是矢量场的闭曲面的面积分（通量），左边是该闭曲面围成的体积的矢量场散度的体积分；
• 闭曲面的面积分，与该闭曲面围成的体积的体积分互化关系；
• 给出了通量的一种计算方法，即使用散度的体积分获得；

矢量场（函数）的环量和旋度

环量的定义
ψ = ∮ s A ⃗ ⋅ d l ⃗ = ∮ s A cos ⁡ θ d l \psi = \oint_s\vec{A} \cdot d\vec{l} = \oint_s A \cos\theta \,dl ψ=∮s​A ⋅dl =∮s​Acosθdl

环量的物理意义

• 从定义式看出是点乘，结果是标量，仅有大小。按点乘几何意义的 A ⃗ \vec{A} A 要向 l ⃗ \vec{l} l 的方向投影，投影后就与面垂直，即垂直于 n ⃗ \vec{n} n 。
• 对于封闭曲线，标量就要考虑大小的几种可能
  $\psi \ne 0$ ：封闭曲线内有涡旋源没有做大于或小于零区分；
  $\psi =0$ ：无旋。对应无旋场；（静电场是无旋场）

环量密度定义

单位面积的环量，即环量面密度：
lim ⁡ Δ V → 0 ∮ c A ⃗ ⋅ d l ⃗ Δ S \begin{align} \underset{\Delta V\to 0}{\lim} \frac{\oint_c\vec{A} \cdot d\vec{l}}{\Delta S} \end{align} ΔV→0lim​ΔS∮c​A ⋅dl ​​​
旋度的定义

环量面密度的最大值；
r o t A ⃗ = n ⃗ lim ⁡ Δ S → 0 ∣ ∮ c A ⃗ ⋅ d l ⃗ ∣ m a x Δ S = ∇ × A ⃗ = ( ∂ ∂ x e ⃗ x + ∂ ∂ y e ⃗ y + ∂ ∂ z e ⃗ z ) × ( A x e ⃗ x + A y e ⃗ y + A z e ⃗ z ) = ∣ e ⃗ x e ⃗ y e ⃗ z ∂ ∂ x ∂ ∂ y ∂ ∂ z A x A y A z ∣ = ( ∂ A z ∂ y − ∂ A y ∂ z ) e ⃗ x + ( ∂ A x ∂ z − ∂ A z ∂ x ) e ⃗ y + ( ∂ A y ∂ x − ∂ A x ∂ y ) e ⃗ z \begin{align} rot\,\vec{A} &= \vec{n} \underset{\Delta S\to 0}{\lim} \frac{{|\oint_c\vec{A} \cdot d\vec{l}|}_{max}} {\Delta S} \\&= \nabla \times \vec{A} \\&= (\frac{\partial}{\partial x}\vec{e}_x + \frac{\partial}{\partial y}\vec{e}_y + \frac{\partial}{\partial z}\vec{e}_z ) \times (A_x\vec{e}_x + A_y\vec{e}_y + A_z\vec{e}_z) \\&= \begin{vmatrix} \vec{e}_x & \vec{e}_y & \vec{e}_z \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ A_x & A_y & A_z \end{vmatrix}\\&= (\frac{\partial A_z}{\partial y} - \frac{\partial A_y}{\partial z})\vec{e}_x + (\frac{\partial A_x}{\partial z} - \frac{\partial A_z}{\partial x})\vec{e}_y + (\frac{\partial A_y}{\partial x} - \frac{\partial A_x}{\partial y})\vec{e}_z \end{align} rotA ​=n ΔS→0lim​ΔS∣∮c​A ⋅dl ∣max​​=∇×A =(∂x∂​e x​+∂y∂​e y​+∂z∂​e z​)×(Ax​e x​+Ay​e y​+Az​e z​)= ​e x​∂x∂​Ax​​e y​∂y∂​Ay​​e z​∂z∂​Az​​ ​=(∂y∂Az​​−∂z∂Ay​​)e x​+(∂z∂Ax​​−∂x∂Az​​)e y​+(∂x∂Ay​​−∂y∂Ax​​)e z​​​

旋度定理（斯托克斯定理）

计算式=定义式。
∇ × A ⃗ = n ⃗ lim ⁡ Δ S → 0 ∣ ∮ c A ⃗ ⋅ d l ⃗ ∣ m a x Δ S \begin{align} \nabla \times \vec{A} &= \vec{n} \underset{\Delta S\to 0}{\lim} \frac{{|\oint_c\vec{A} \cdot d\vec{l}|}_{max}} {\Delta S} \\ \end{align} ∇×A ​=n ΔS→0lim​ΔS∣∮c​A ⋅dl ∣max​​​​
右边的 $\Delta S$ 和极限符号移到左边，并对左边面积分得到

∫ s ∇ × A ⃗ ⋅ d S ⃗ = ∮ c A ⃗ ⋅ d l ⃗ \int_s \nabla \times \vec{A} \cdot d\vec{S} =\oint_c\vec{A} \cdot d\vec{l} ∫s​∇×A ⋅dS =∮c​A ⋅dl
提示：

• 积分方程组和微分方程组的互化纽带；
• 右边是矢量场的闭曲线的线积分（环量），左边是该闭曲面围成的面积的矢量场旋度的面积分；
• 闭曲线的线积分，与该闭曲线围成的面积的面积分互化关系；
• 给出了环量的一种计算方法，即使用旋度的面积分获得；

两个重要恒等式

• 标量场的梯度的旋度恒等于０矢量
  ∇ × ( ∇ φ ) = 0 ⃗ \nabla \times (\nabla \varphi) = \vec{0} ∇×(∇φ)=0

• 矢量场的旋度的散度恒等于０标量
  ∇ ⋅ ( ∇ × A ⃗ ) = 0 ⃗ \nabla \cdot (\nabla \times \vec{A}) = \vec{0} ∇⋅(∇×A )=0

1.4 亥姆霍兹定理

亥姆霍兹定理：矢量场 F ⃗ \vec{F} F 在无限空间中处处单值，且其导数连续有界，而源分布在有限空间区域中，则矢量场由其散度和旋度唯一确定，并且表示为两个矢量场之和 F ⃗ = F ⃗ 1 + F ⃗ 2 \vec{F}=\vec{F}_1+\vec{F}_2 F =F 1​+F 2​ ，其中 为 F ⃗ 1 \vec{F}_1 F 1​ 一个标量场 $\phi$ 的负梯度， F ⃗ 2 \vec{F}_2 F 2​ 为一个矢量场 A ⃗ \vec{A} A 的旋度。

提示：负梯度中的负号是人为引入，在后面会看到，标量场 $\phi$ 表示电位，而一般是选取无限远处电位为零。

数学公式表述：
F ⃗ = F ⃗ 1 + F ⃗ 2 F ⃗ 1 = − ∇ φ F ⃗ 2 = ∇ × A ⃗ F ⃗ = − ∇ φ + ∇ × A ⃗ \begin{align} &\vec{F} = \vec{F}_1 + \vec{F}_2 \\ &\vec{F}_1 = -\nabla \varphi \\ &\vec{F}_2 = \nabla \times \vec{A} \\ &\vec{F} = -\nabla \varphi + \nabla \times \vec{A} \\ \end{align} ​F =F 1​+F 2​F 1​=−∇φF 2​=∇×A F =−∇φ+∇×A ​​
分解后的意义：

• 研究矢量场 F ⃗ \vec{F} F 转去研究矢量场的分量 F ⃗ 1 \vec{F}_1 F 1​ 和 F ⃗ 2 \vec{F}_2 F 2​，进一步要研究标量场 $\phi$ 和矢量场 A ⃗ \vec{A} A ，在后面时变电磁场会看到和有一定的关系，而只需研究一个即可。

• 分解后两个矢量场的特点：
  ∇ × F ⃗ 1 = − ∇ × ( ∇ φ ) = 0 ⃗ ∇ ⋅ F ⃗ 2 = ∇ ⋅ ( ∇ × A ⃗ ) = 0 \begin{align} \nabla \times\vec{F}_1 &= - \nabla \times (\nabla\varphi )\\ &=\vec{0} \\\\ \nabla\cdot\vec{F}_2 &= \nabla \cdot (\nabla \times \vec{A}) \\ &={0} \end{align} ∇×F 1​∇⋅F 2​​=−∇×(∇φ)=0 =∇⋅(∇×A )=0​​
  说明分解后的场一个是无旋场，一个是无源场。

矢量场由其散度和旋度唯一确定
F ⃗ = F ⃗ 1 + F ⃗ 2 { ∇ ⋅ F ⃗ = ∇ ⋅ F ⃗ 1 + ∇ ⋅ F ⃗ 2 = ∇ ⋅ F ⃗ 2 = 0 ∇ ⋅ F ⃗ 1 = 令 ρ ε ∇ × F ⃗ = ∇ × F ⃗ 1 + ∇ × F ⃗ 2 = ∇ × F ⃗ 1 = 0 ∇ × F ⃗ 2 = 令 0 ⃗ \begin{align} &\,\,\,\,\,\vec{F} = \vec{F}_1 + \vec{F}_2 \\ &\begin{cases} \nabla\cdot\vec{F} &= \nabla\cdot\vec{F}_1 &+ \nabla\cdot\vec{F}_2 \, &{\xlongequal{\nabla\cdot\vec{F}_2 =0}} &\nabla\cdot\vec{F}_1 &\xlongequal{令} \frac{\rho}{\varepsilon} \\ \nabla \times \vec{F} &= \nabla \times \vec{F}_1 &+ \nabla \times \vec{F}_2 \, &{\xlongequal{\nabla \times \vec{F}_1 = 0}} &\nabla \times \vec{F}_2 &\xlongequal{令} \vec{0} \end{cases} \\ \\ \end{align} ​F =F 1​+F 2​{∇⋅F ∇×F ​=∇⋅F 1​=∇×F 1​​+∇⋅F 2​+∇×F 2​​∇⋅F 2​=0 ∇×F 1​=0 ​∇⋅F 1​∇×F 2​​令 ερ​令 0 ​​​
则有
{ ∇ ⋅ F ⃗ = ρ ε ∇ × F ⃗ = 0 ⃗ \begin{cases} \nabla \cdot \vec{F} &= \frac{\rho}{\varepsilon} \\ \nabla \times \vec{F} &= \vec{0} \end{cases} {∇⋅F ∇×F ​=ερ​=0 ​
使用静电场代替矢量场 E ⃗ → F ⃗ \vec{E}\to\vec{F} E →F ，则可得到静电场的场方程
{ ∇ ⋅ E ⃗ = ρ ε ∇ × E ⃗ = 0 ⃗ \begin{cases} \nabla \cdot \vec{E} &= \frac{\rho}{\varepsilon} \\ \nabla \times \vec{E} &= \vec{0} \end{cases} {∇⋅E ∇×E ​=ερ​=0 ​
在直角坐标系下具体化展开
{ ∂ ∂ x e ⃗ x + ∂ ∂ y e ⃗ y + ∂ ∂ z e ⃗ z ) ⋅ ( E x e ⃗ x + E y e ⃗ y + E z e ⃗ z ) = ρ ε ∣ e ⃗ x e ⃗ y e ⃗ z ∂ ∂ x ∂ ∂ y ∂ ∂ z E x E y E z ∣ = 0 ⃗ \begin{align} \begin{cases} \frac{\partial}{\partial x}\vec{e}_x + \frac{\partial}{\partial y}\vec{e}_y + \frac{\partial}{\partial z}\vec{e}_z ) \cdot (E_x\vec{e}_x + E_y\vec{e}_y + E_z\vec{e}_z) = \frac{\rho}{\varepsilon} \\ \\ \begin{vmatrix} \vec{e}_x & \vec{e}_y & \vec{e}_z \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ E_x & E_y & E_z \end{vmatrix} = \vec{0} \end{cases} \end{align} ⎩ ⎨ ⎧​∂x∂​e x​+∂y∂​e y​+∂z∂​e z​)⋅(Ex​e x​+Ey​e y​+Ez​e z​)=ερ​ ​e x​∂x∂​Ex​​e y​∂y∂​Ey​​e z​∂z∂​Ez​​ ​=0 ​​​

{ ∂ E x ∂ x + ∂ E y ∂ y + ∂ E z ∂ z = ρ ε ( ∂ E z ∂ y − ∂ E y ∂ z ) e ⃗ x + ( ∂ E x ∂ z − ∂ E z ∂ x ) e ⃗ y + ( ∂ E y ∂ x − ∂ E x ∂ y ) e ⃗ z = 0 ⃗ \begin{cases} \frac{\partial E_x}{\partial x} + \frac{\partial E_y}{\partial y} + \frac{\partial E_z}{\partial z} = \frac{\rho}{\varepsilon} \\ \\ (\frac{\partial E_z}{\partial y} - \frac{\partial E_y}{\partial z})\vec{e}_x + (\frac{\partial E_x}{\partial z} - \frac{\partial E_z}{\partial x})\vec{e}_y + (\frac{\partial E_y}{\partial x} - \frac{\partial E_x}{\partial y})\vec{e}_z = \vec{0} \end{cases} ⎩ ⎨ ⎧​∂x∂Ex​​+∂y∂Ey​​+∂z∂Ez​​=ερ​(∂y∂Ez​​−∂z∂Ey​​)e x​+(∂z∂Ex​​−∂x∂Ez​​)e y​+(∂x∂Ey​​−∂y∂Ex​​)e z​=0 ​

解出三个分量，得到矢量场，尤其散度和旋度唯一确定。

1.5 三种坐标系

1.5.1 直角坐标系

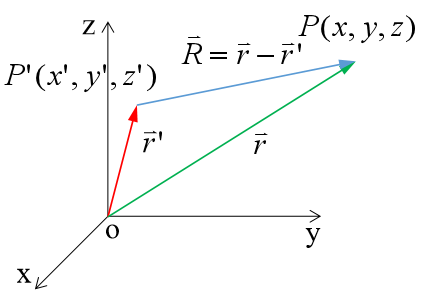
1.5.2 柱坐标系

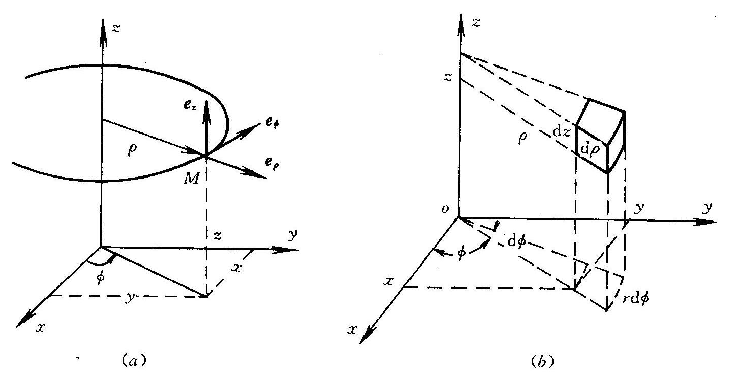
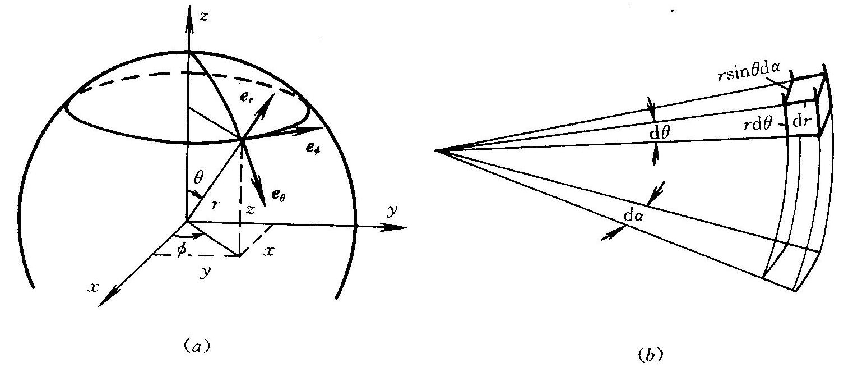
1.5.3 球坐标系

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！