【基础】自动驾驶控制算法第三讲 轮胎侧偏与车辆动力学方程

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

文章目录

• 前言
• 一、为啥不用运动学方程？
• 动力学方程
• • • 纵向控制
    • 横向控制
• 二自由度动力学方程
• • 假设
  • • 轮胎的侧偏特性（一种清新脱俗的解释）
  • 自行车模型推导
• 总结

前言

信息来源于B站 忠厚老实的老王，侵删。

提示：以下是本篇文章正文内容，下面案例可供参考

一、为啥不用运动学方程？

• 简化太多
• 非线性方程
• 纵向速度和方向盘转角耦合

用途： 坐标变换（注意这里忽略了侧偏角的速度）（）

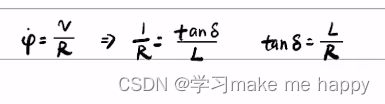
动力学方程

• 考虑了轮胎的特性
• 商业化的自动驾驶算法都是以动力学方程为基础

• 关于a_n，使用了运动学得到的公式，相对于横摆角，侧偏角变化率比较小，这个情况适用于高速，所以可以用这个公式。
• 但，tan（delta）这个公式没有考虑轮胎的侧偏特性，所以这个模型用来做高速运动控制不够（有时间再吸收一下）
• 图片红字部分说明的是横纵向的解耦。说白了，一个负责改变速度的大小，一个负责改变速度的方向。
• 黑子部分介绍了运动学模型中的耦合。

纵向控制

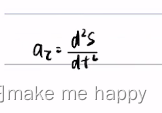
横向控制

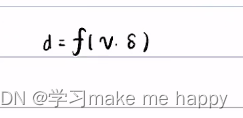
求解思路：

二自由度动力学方程

假设

1. 前轮转角比较小
2. v_x（车辆坐标系下）是常数

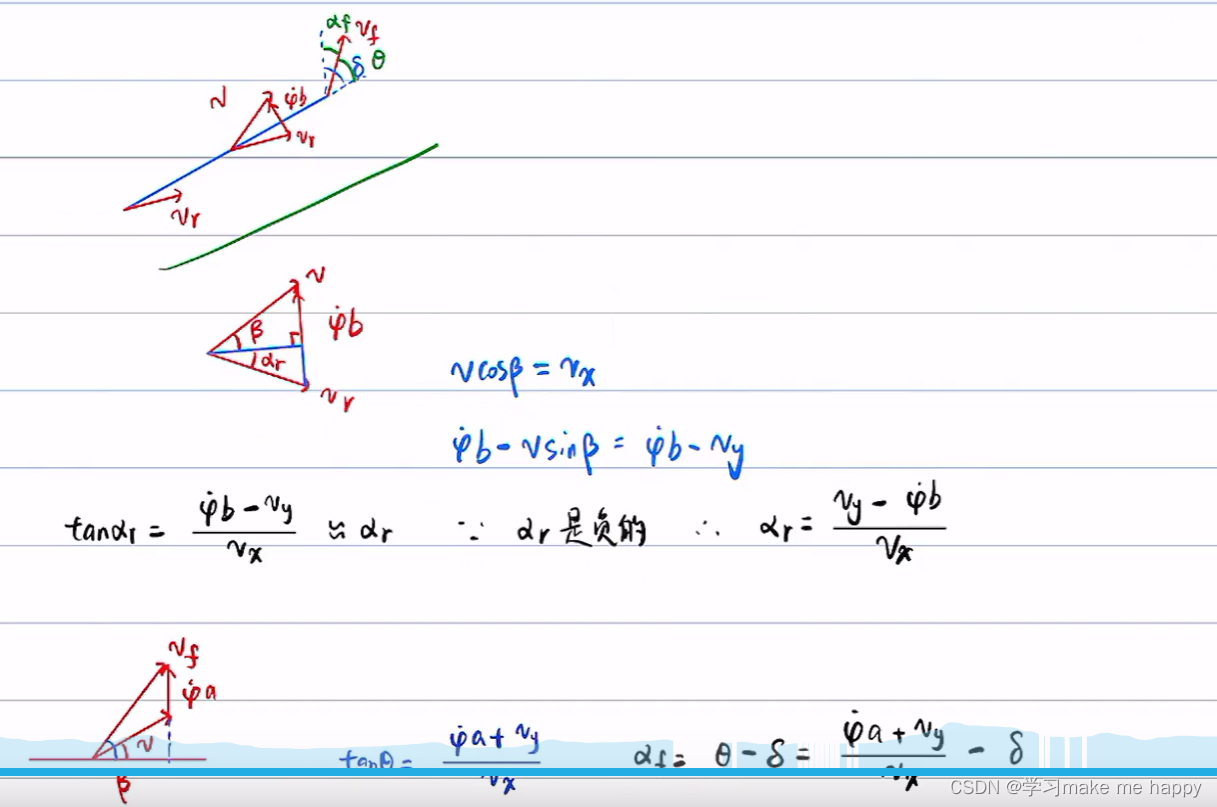
轮胎的侧偏特性（一种清新脱俗的解释）

下图讲的是轮胎侧偏的等效


上图适用于非极限工况。

自行车模型推导

下图中up猪漏了一项，自己找一下吧。

下面做了一个重要的假设。

然而，我们并不满足于此，我们需要下面的关系。

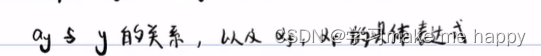
下面是dotdota_y带小尾巴的解释


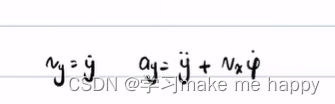
下面是求侧偏角的过程，利用的也是理论力学的知识。

推导出来的动力学模型

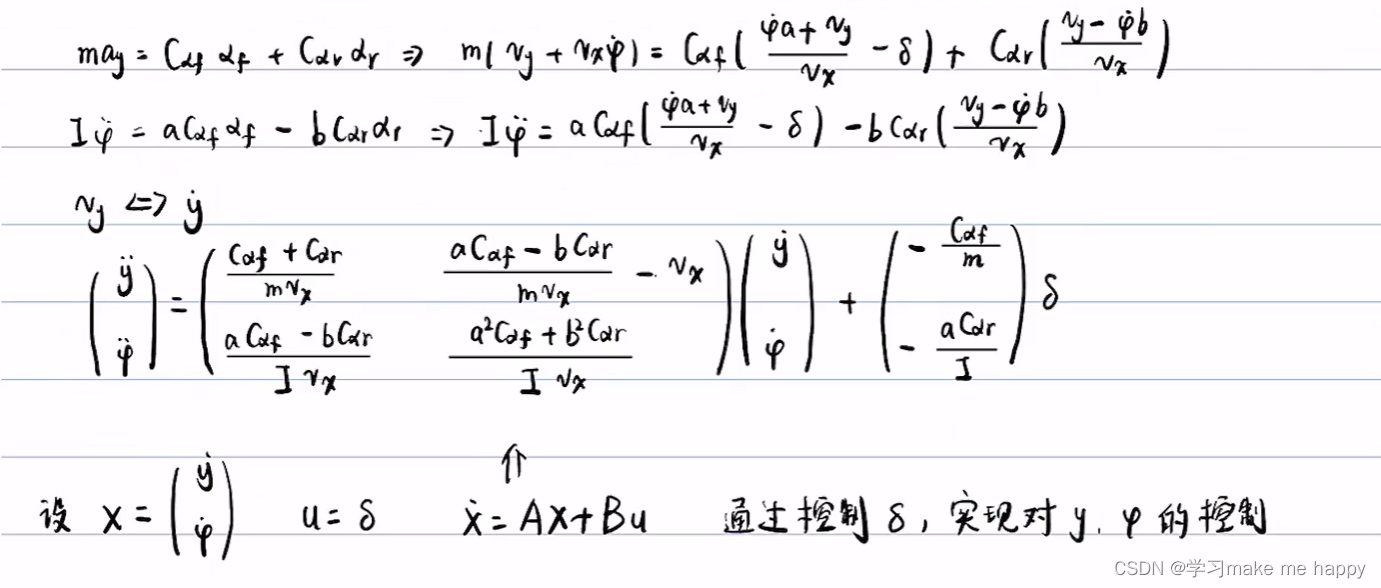
总结

感谢老王。
本课中还有一些知识点需要消化吸收。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！