matlab奇偶分解_【 MATLAB 】序列的奇偶分解的 MATLAB 函数编写实践
序列 x(n)的奇偶分解的公式为:
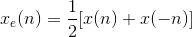
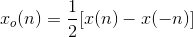
编写一个序列 x(n) 的奇偶分解式 xe(n) 和 xo(n),需要考虑的问题是序列长度,下标的变化。
这里必须做个声明,下面的程序中用到了前几篇博客中的几个函数,这里给贴出来:
信号相加:
function [y,n] = sigadd(x1,n1,x2,n2)
% implements y(n) = x1(n) + x2(n)
% [y,n] = sigadd(x1,n1,x2,n2)
%____________________________________
% y = sum sequence over n, which includes n1 and n2
% x1 = first sequence over n1
% x2 = second sequence over n2( n2 can be different from n1)
%
n = min( min(n1), min(n2) ):max( max(n1), max(n2) ); %duration of y(n)
y1 = zeros(1,length(n)); y2 = y1; %initialization
y1( find( ( n >= min(n1) )&( n <= max(n1) ) == 1 ) ) = x1; %x1 with duration of y1
y2( find( ( n >= min(n2) )&( n <= max(n2) ) == 1 ) ) = x2; %x2 with duration of y2
y = y1 + y2;
信号移位:
function [y,n] = sigshift(x,m,k)
%implements y(n) = x(n - k)
%_________________________
%[y,n] = sigshift(x,m,k)
%
n = m+k;
y = x;
单位阶跃序列:
function [x,n]=stepseq(n0,n1,n2);
% generate x(n) = u(n - n0); n1 <= n <= n2
%_____________________________________________
%[x,n] = stepseq(n0, n1, n2);
%
n = [n1:n2];
x = [(n-n0) >= 0];
下面给出函数程序:
function [xe, xo, m] = evenodd(x, n)
% Real signal decomposition into even and odd parts
%__________________________________________________
%[xe, xo, m] = evenodd(x, n)
%
if any( imag(x) )
error('x is not a real sequence!');
end
% Ensure m of xe and xo
m = - fliplr(n);
m1 = min([m,n]);
m2 = max([m,n]);
m = m1:m2;
% Ensure x over m
nm = n(1) - m(1);
n1 = 1:length(n);
x1 = zeros(1,length(m)); % initialization
x1(nm + n1) = x;
x = x1; % new x which enlarge index n
% xe and xo
xe = 0.5*(x + fliplr(x));
xo = 0.5*(x - fliplr(x));
序列和及其位置分别装入 x 和 n 数组。首先确认是否已知序列是实序列并在m数组中确定偶部和奇部分量的位置,最后将所得奇偶分量存入xe和xo数组中。
下面以一个实例来验证上述函数:
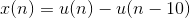
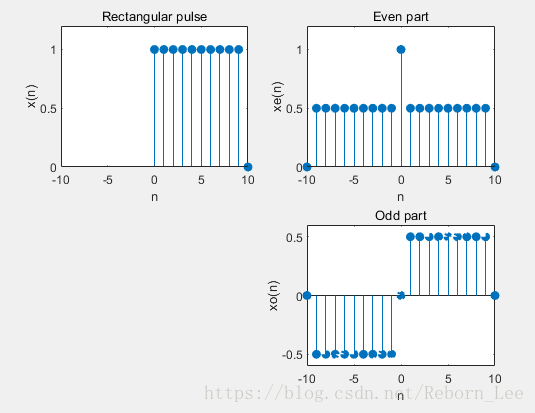
将x(n)分解为奇偶分量。
clc
clear
close all
n = 0:10;
x = stepseq(0,0,10) - stepseq(10,0,10);
[xe, xo, m] = evenodd(x,n);
subplot(2,2,1);
stem(n,x,'filled');
title('Rectangular pulse');
xlabel('n');ylabel('x(n)');
axis([-10,10,0,1.2]);
subplot(2,2,2);
stem(m,xe,'filled');
title('Even part');
xlabel('n');ylabel('xe(n)');
axis([-10,10,0,1.2]);
subplot(2,2,4);
stem(m,xo,'filled');
title('Odd part');
xlabel('n');ylabel('xo(n)');
axis([-10,10,-0.6,0.6]);
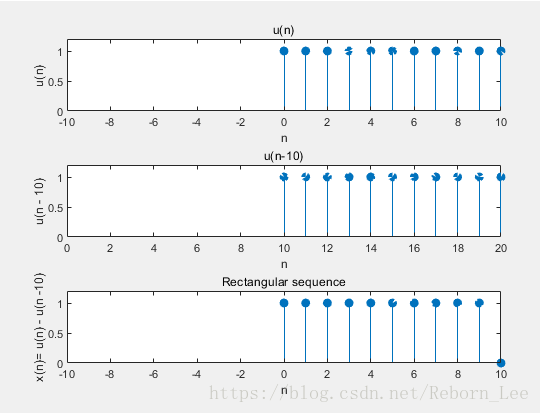
事实上,这篇博文到这里已经结束了,那我还想看看序列x(n)= u(n) - u(n-10)的合成过程:
clc
clear
close all
[u1,n1] = stepseq(0,0,10);
subplot(3,1,1)
stem(n1,u1,'filled');
title('u(n)');
ylabel('u(n)');xlabel('n');
axis([-10,10,0,1.2]);
[u2,n2] = sigshift(u1,n1,10);
subplot(3,1,2)
stem(n2,u2,'filled');
title('u(n-10)')
xlabel('n');ylabel('u(n - 10)');
axis([0,20,0,1.2]);
[x,n] = sigadd(u1,n1,-u2,n2);
subplot(3,1,3)
stem(n,x,'filled');
title('Rectangular sequence');
xlabel('n');ylabel('x(n)= u(n) - u(n -10)');
axis([-10,10,0,1.2]);
本文同步分享在 博客“李锐博恩”(CSDN)。
如有侵权,请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”,欢迎正在阅读的你也加入,一起分享。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!