MATH-现代-行列式

克拉默法则

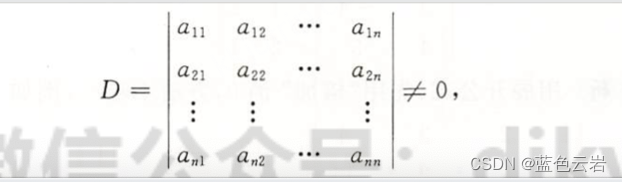
1. 如果一个方程组的系数行列式不等于零
   

2. 则方程组有唯一一组解
   
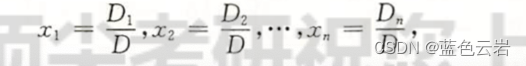
   D是系数矩阵
   
   Di是用方程右边的直组成的列替换系数矩阵的第i列得到的矩阵

推论1: 如果齐次方程组的系数矩阵行列式不为零，则该行列式只有0解
推论2: 如果齐次方程组有非零解，系数矩阵行列式一定等于零

特殊行列式

1. 主对角线上下三角矩阵-等于主对角线元素的积
   2. 主对角线：从左上到右下

2. 副对角线矩阵-等于副对角线元素的积，正负取决于（交换次数）的奇偶行

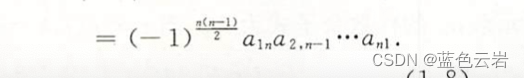
3. 拉普拉斯展开式
   

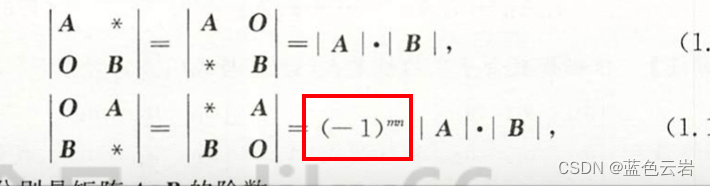
4. 范德门行列式
   
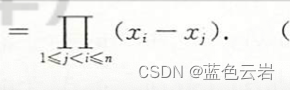
   从右往左，从下往上依次减一遍

方阵的行列式的性质

1. 转置矩阵行列式不变
2. ｜kA｜= kn|A|，矩阵的数乘的行列式等于该数的n次方乘以该矩阵的行列式
   3. 矩阵乘积的行列式=行列式的乘积
   4. 逆矩阵的行列式等于矩阵的行列式的倒数
   5. |A| = ｜A｜的n-1次方*
   6. 矩阵特征值的乘积等于矩阵行列式的值
3. 相似矩阵行列式相同，相似矩阵加上k倍的单位矩阵的行列式也相同

余子式和代数余子式

1. n阶行列式=任意一行的元素和对应的代数余子式的乘积之和
   
2. 任意一行或者一列和不同于它的一行或列的代数余子式的乘积位0
3. 根据以上两个性质可以推出，AA* = |A|E，只有对应的元素和余子式的乘积=｜A｜，其他都是0
   
   余子式是去除该元素剩下的行列式，代数余子式有一个系数，二者可以通过该系数转化

行列式完全展开式

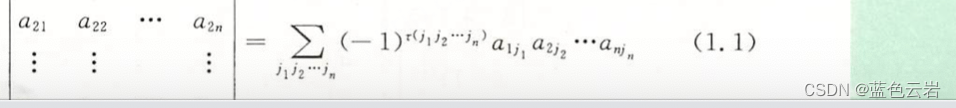
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！