蒙特卡洛树搜索及实现三子棋游戏

蒙特卡洛树搜索及实现三子棋游戏

预备知识

双人有限零和顺序游戏

MCTS运行所在的框架/环境是一个游戏，它本身是一个非常抽象和宽泛的概念，因此这里我们只关注一种游戏类型：双人有限零和顺序游戏。这个名词一开始听起来会有些复杂，但是实际上非常简单，现在来让我们将它分解一下：

游戏：意味着我们在一种需要交互的情境中，交互通常会涉及一个或多个角色
有限：表明在任意时间点，角色之间存在的交互方式都是有限的
双人：游戏中只有两个角色
顺序：玩家依次交替进行他们的动作
零和：参与游戏的两方有完全相反的目标，换句话说就是，游戏的任意结束状态双方的收益之和等于零
  我们可以很轻松的验证，围棋、国际象棋和井字棋都是双人有限零和顺序游戏：有两位玩家参与，玩家能进行的动作总是有限的，双方的游戏目标是完全相反的（所有游戏的结果之和等于0）

原文链接：https://blog.csdn.net/qq_16137569/article/details/83543641

游戏树

游戏树是一种常见的数据结构,其中每一个节点代表游戏的一个确定状态,从一个节点到该节点的一个子节点（如果存在）是一个移动。节点的子节点数目称为分支因子。游戏树的根节点代表游戏的初始状态。游戏树的终端节点是没有子节点的节点，至此游戏结束，无法再进行移动。终端节点的状态也就是游戏的结果（输/赢/平局）。

下面以井字棋游戏为例，形象地来看下什么是游戏树。

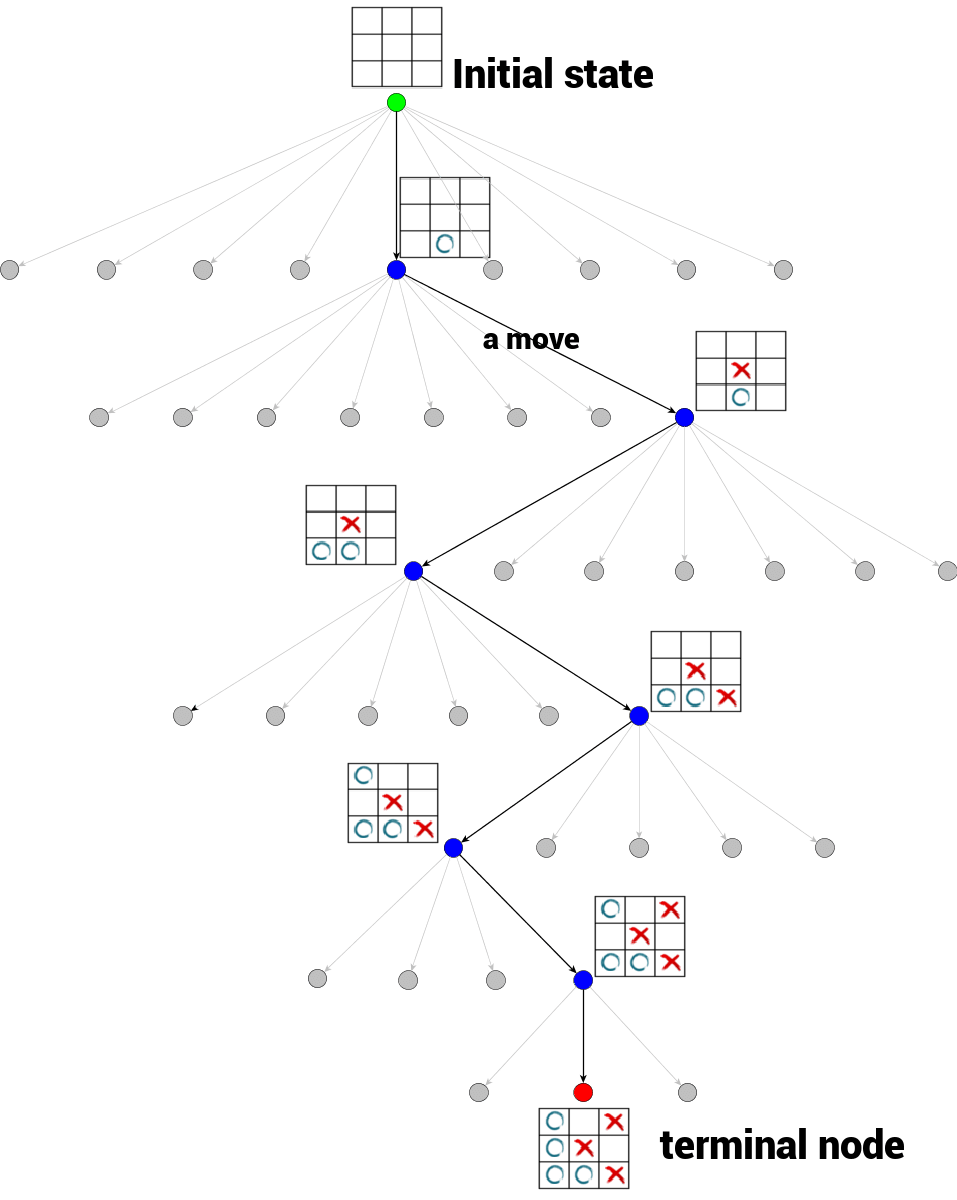
每个父节点的子节点数量对应着本次可以执行的Action的数量

蒙特卡洛树搜索

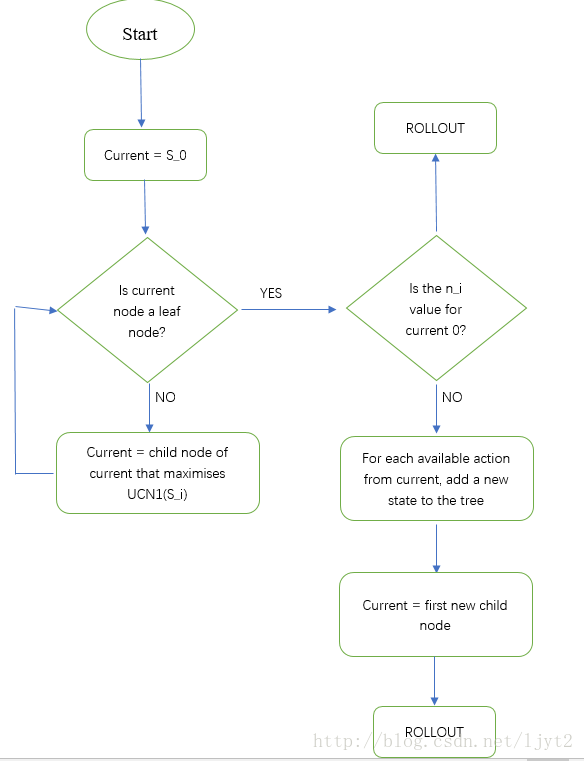
搜索流程图

搜索步骤

1. 选择
   从根节点开始，我们选择采用UCB计算得到的最大的值的孩子节点，如此向下搜索，直到我们来到树的底部的叶子节点(没有孩子节点的节点),若果该节点没有子节点,就会去执行扩展

2. 扩展
   到达叶子节点后，如果还没有到达终止状态，那么我们就要对这个节点进行扩展(这里是一个迭代过程)，扩展出一个或多个节点。可以扩展一个节点也可以扩展多个节点.

3. 模拟
   我们基于目前的这个状态，根据某一种策略（例如random policy）进行模拟，直到游戏结束为止，产生结果，比如胜利或者失败。此处的模拟可以指定模拟多少轮也可以指定模拟多少时间.所以模拟的本质还是用频率去逼近概率

4. 反向传播

   根据模拟的结果，我们要自底向上，反向更新所有节点的信息.一般需要更新的值有该节点被访问的次数和该节点的奖励值.若模拟结果为胜利,则奖励为正,模拟结果为失败,则奖励为负.奖励函数也可以设计的很复杂

每次搜索步骤需要N次的模拟,但只对应了一次下棋,每次下棋后都会更新状态,并从新状态开始(人也下完了棋),进行下一次的搜索.(下一步棋)

具体案例可以看博客

节点状态

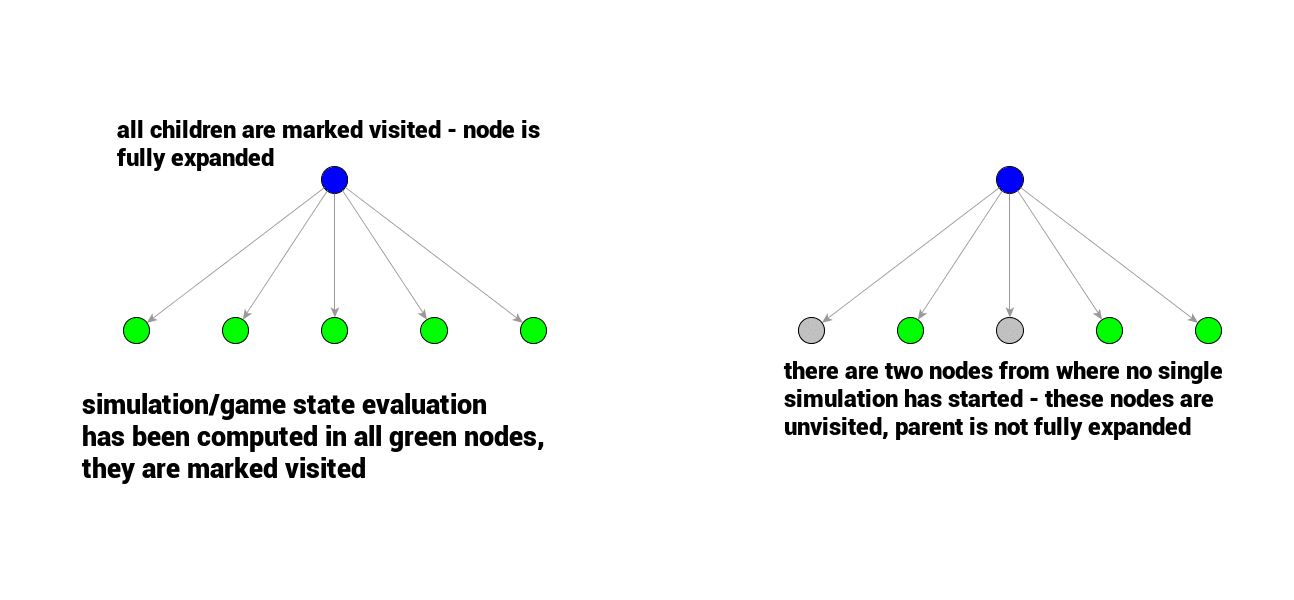
某个节点的所有子节点全都被访问过,则该节点称作完全扩展,否则就是未完全扩展.

图中灰色的节点表示被扩展出来但是还没有被访问过

UCT计算

U C T ( v i , v ) = Q ( v i ) N ( v i ) + c log ⁡ ( N ( v ) ) N ( v i ) \mathbb{U C} \mathbb{T}\left(v_{i}, v\right)=\frac{Q\left(v_{i}\right)}{N\left(v_{i}\right)}+c \sqrt{\frac{\log (N(v))}{N\left(v_{i}\right)}} UCT(vi​,v)=N(vi​)Q(vi​)​+cN(vi​)log(N(v))​ ​

($N(vi)$ 是节点被访问的次数，而 $N(v)$ 则是其父节点已经被访问的总次数)

UCT的第一部分是(总收益/总次数=平均每次的收益）,即优先选择收益大的.但只有这一项是不够的,那些未被选中的节点之后就再也无法选到了,

UCT的第二部分是倾向于那些未被探索的节点,(子节点被探索的越少则分母越小,)

c是一个常数,用于平衡两部分的值

何时停止

原则上,模拟的次数越多则结果越好,但在实际中往往会指定一个时间限制或是模拟次数限制,防止运行时间过长(比如跟你对战的ai迟迟不下棋).在模拟结束后,最佳的移动通常是访问次数最多的那个节点.

代码实现

实现一个三子棋程序

其中蒙特卡洛树代码来自git

蒙特卡洛核心类

1. mcts类:

   search方法对应模拟方法

   executeRound方法定义了一次模拟流程

   selectNode对应节点选择,

   • 该节点若有子节点,则使用getBestChild方法获得UCT值最大的节点
   • 若无子节点,则使用expand方法扩展子节点

   rollout方法将在选择的节点上随机执行一种Action

   backpropogate方法对应反向传播

   getBestChild,在n次executeRound执行完后,选择子节点中最优的

   getAction方法是从子节点中获取其动作(下到哪里)

2. treeNode类,用于构建树形结构,存储当前节点的状态

3. randomPolicy方法:规定了rollout时使用哪种方式,一般使用随机选择的方式

from __future__ import divisionimport time
import math
import randomdef randomPolicy(state):while not state.isTerminal():try:action = random.choice(state.getPossibleActions())except IndexError:raise Exception("Non-terminal state has no possible actions: " + str(state))state = state.takeAction(action)return state.getReward()class treeNode():def __init__(self, state, parent):self.state = stateself.isTerminal = state.isTerminal()self.isFullyExpanded = self.isTerminalself.parent = parentself.numVisits = 0self.totalReward = 0self.children = {}class mcts():def __init__(self, timeLimit=None, iterationLimit=None, explorationConstant=1 / math.sqrt(2),rolloutPolicy=randomPolicy):if timeLimit != None:if iterationLimit != None:raise ValueError("Cannot have both a time limit and an iteration limit")# time taken for each MCTS search in millisecondsself.timeLimit = timeLimitself.limitType = 'time'else:if iterationLimit == None:raise ValueError("Must have either a time limit or an iteration limit")# number of iterations of the searchif iterationLimit < 1:raise ValueError("Iteration limit must be greater than one")self.searchLimit = iterationLimitself.limitType = 'iterations'self.explorationConstant = explorationConstantself.rollout = rolloutPolicydef search(self, initialState):self.root = treeNode(initialState, None)if self.limitType == 'time':  # 时间限制timeLimit = time.time() + self.timeLimit / 1000while time.time() < timeLimit:self.executeRound()else:  # 次数限制for i in range(self.searchLimit):self.executeRound()# executeRound执行完后,其叶子节点就存放了他们的信息bestChild = self.getBestChild(self.root, 0)return self.getAction(self.root, bestChild)def executeRound(self):node = self.selectNode(self.root) reward = self.rollout(node.state)self.backpropogate(node, reward)def selectNode(self, node):while not node.isTerminal: # 这里会一直找到游戏结束,即最后一个节点if node.isFullyExpanded:node = self.getBestChild(node, self.explorationConstant)else:return self.expand(node)  # 每次把所有的孩子都扩展出来return nodedef expand(self, node):actions = node.state.getPossibleActions()for action in actions:if action not in node.children:newNode = treeNode(node.state.takeAction(action), node) node.children[action] = newNodeif len(actions) == len(node.children):node.isFullyExpanded = Truereturn newNoderaise Exception("Should never reach here")def backpropogate(self, node, reward):while node is not None:node.numVisits += 1node.totalReward += rewardnode = node.parentdef getBestChild(self, node, explorationValue):bestValue = float("-inf")bestNodes = []for child in node.children.values():nodeValue = child.totalReward / child.numVisits + explorationValue * math.sqrt(2 * math.log(node.numVisits) / child.numVisits)if nodeValue > bestValue:bestValue = nodeValuebestNodes = [child]elif nodeValue == bestValue:bestNodes.append(child)return random.choice(bestNodes)def getAction(self, root, bestChild):for action, node in root.children.items():if node is bestChild:return action

状态类

1. Action类是动作类,封装了执行的动作,比如下棋到哪个位置
2. NaughtsAndCrossesState类是状态类,要提供以下方法
   1. 维护玩家状态: currentPlayer
   2. 维护棋盘状态: board
   3. 提供一个获得所有可行状态的方法getPossibleActions
   4. 提供一个执行Action的方法takeAction,并且要更新自己的状态
   5. 提供一个isTerminal函数,用于判断游戏是否结束
   6. 提供一个getReward方法,用于计算奖励

from __future__ import divisionfrom copy import deepcopy
from mcts import mcts
from functools import reduce
import operatorclass NaughtsAndCrossesState(object):def __init__(self):self.target_num = 3  # 最终目标self.board_width = 3self.board = [[0] * self.board_width for _ in range(self.board_width)]self.currentPlayer = 1def getPossibleActions(self):possibleActions = []for i in range(len(self.board)):for j in range(len(self.board[i])):if self.board[i][j] == 0:possibleActions.append(Action(player=self.currentPlayer, x=i, y=j))return possibleActionsdef takeAction(self, action):newState = deepcopy(self)newState.board[action.x][action.y] = action.playernewState.currentPlayer = self.currentPlayer * -1return newStatedef isTerminal(self):for row in self.board:if abs(sum(row)) == self.target_num:return Truefor column in list(map(list, zip(*self.board))):if abs(sum(column)) == self.target_num:return Truefor diagonal in [[self.board[i][i] for i in range(len(self.board))],[self.board[i][len(self.board) - i - 1] for i in range(len(self.board))]]:if abs(sum(diagonal)) == self.target_num:return Truereturn reduce(operator.mul, sum(self.board, []), 1)def getReward(self):for row in self.board:if abs(sum(row)) == self.target_num:return sum(row) / self.target_numfor column in list(map(list, zip(*self.board))):if abs(sum(column)) == self.target_num:return sum(column) / self.target_numfor diagonal in [[self.board[i][i] for i in range(len(self.board))],[self.board[i][len(self.board) - i - 1] for i in range(len(self.board))]]:if abs(sum(diagonal)) == self.target_num:return sum(diagonal) / self.target_numreturn Falseclass Action():def __init__(self, player, x, y):self.player = playerself.x = xself.y = ydef __str__(self):return str((self.x, self.y))def __repr__(self):return str(self)def __eq__(self, other):return self.__class__ == other.__class__ and self.x == other.x and self.y == other.y and self.player == other.playerdef __hash__(self):return hash((self.x, self.y, self.player))if __name__ == '__main__':import numpy as nps = NaughtsAndCrossesState()tree = mcts(timeLimit=1000)while True:# 机器下棋action = tree.search(initialState=s)s = s.takeAction(action)print("ai:", action)print(np.array(s.board))if s.isTerminal():print("ai win")break# 人下棋x, y = list(map(int, input().split()))action = Action(-1, x, y)s = s.takeAction(action)print("人:", action)print(np.array(s.board))print(s.isTerminal())if s.isTerminal():print("human win")break

我们在实际使用中,只需定义一个合适的State和Action类并实现其方法,就可以应用到mcts中.不要将State和Action耦合在MCTS中,这样就没有扩展性了

参考博客

面向初学者的蒙特卡洛树搜索MCTS详解及其实现

MCTS蒙特卡洛搜索树实现井字棋游戏

蒙特卡洛树搜索（新手教程）

博客

视频地址

git代码地址

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！