Adaptive Graph Convolutional Recurrent Network for Traffic Forecasting

研究问题

自适应捕捉交通流时间序列中的时空依赖问题

背景动机

• 当前的大多数深度学习方法基于共享参数模型（不同节点对应同一卷积），由于每条道路的 具体情况不一样，这种方式无法捕捉细粒度的数据模式
• 现存方法要求根据距离或相似度预先定义一个图来捕捉空间相关性，这个图不一定能完善地表示空间依赖

模型思想

• 设计节点自适应参数学习(NAPL)模块，分解传统GCN中的参数，根据节点嵌入从所有节点共享的权重池和偏差池生成特定节点参数以捕获节点特定模式
• 设计数据自适应图生成(DAGG)模块，自动推断不同序列之间的相互依赖关系
• 提出一种自适应图卷积递归网络(AGCRN)，基于这两个模块和RNN架构自动捕获交通序列的细粒度时空关联。

符号定义

N个节点在t个时刻的时间序列可以表示为 X = { X : , 0 , X : , 1 , … , X : , t , … } \mathcal{X}=\left\{\boldsymbol{X}_{:, 0}, \boldsymbol{X}_{:, 1}, \ldots, \boldsymbol{X}_{:, t}, \ldots\right\} X={X:,0​,X:,1​,…,X:,t​,…}，其中 X : , t = { x 1 , t , x 2 , t , … , x i , t , … x N , t } T ∈ R N × 1 \boldsymbol{X}_{:, t}=\left\{x_{1, t}, x_{2, t}, \ldots, x_{i, t}, \ldots x_{N, t}\right\}^{T} \in R^{N \times 1} X:,t​={x1,t​,x2,t​,…,xi,t​,…xN,t​}T∈RN×1，目标是学习一个预测函数，使得

{ X : , t + 1 , X : , t + 2 , … , X : , t + τ } = F θ ( X : , t , X : , t − 1 , … , X : , t − T + 1 ; G ) \left\{\boldsymbol{X}_{:, t+1}, \boldsymbol{X}_{:, t+2}, \ldots, \boldsymbol{X}_{:, t+\boldsymbol{\tau}}\right\}=\mathcal{F}_{\boldsymbol{\theta}}\left(\boldsymbol{X}_{:, \boldsymbol{t}}, \boldsymbol{X}_{:, t-1}, \ldots, \boldsymbol{X}_{:, t-\boldsymbol{T}+1} ; \mathcal{G}\right) {X:,t+1​,X:,t+2​,…,X:,t+τ​}=Fθ​(X:,t​,X:,t−1​,…,X:,t−T+1​;G)

其中$$\mathcal{G}=(\mathcal{V},\mathcal{E},\mathbf{A})$$

模型结构

• 节点自适应参数学习(NAPL)模块

传统GCN的计算公式如下

Z = ( I N + D − 1 2 A D − 1 2 ) X Θ + b Z=\left(\boldsymbol{I}_{\boldsymbol{N}}+\boldsymbol{D}^{-\frac{1}{2}} \boldsymbol{A} \boldsymbol{D}^{-\frac{1}{2}}\right) \boldsymbol{X} \boldsymbol{\Theta}+\mathbf{b} Z=(IN​+D−21​AD−21​)XΘ+b

假设 A ∈ R N × N A \in R^{N \times N} A∈RN×N， X ∈ R N × C X \in R^{N \times C} X∈RN×C， Θ ∈ R C × F \Theta \in R^{C \times F} Θ∈RC×F, Z ∈ R N × F Z \in R^{N \times F} Z∈RN×F可以看到，所有节点的特征都经过共同的参数$$\Theta$$处理后从C维变成了F维。为了获取节点特异的参数，一个直观的想法是令 Θ ∈ R N × C × F \Theta \in R^{N \times C \times F} Θ∈RN×C×F,但这样会在N较大的情况下引入过多参数。因此，作者采取了矩阵分解的技巧，令 E G ∈ R N × d , W G ∈ R d × C × d E_G \in R^{N \times d}, W_G \in R^{d \times C \times d} EG​∈RN×d,WG​∈Rd×C×d，GCN计算公式变为

Z = ( I N + D − 1 2 A D − 1 2 ) X E G W G + E G b G Z=\left(I_{N}+D^{-\frac{1}{2}} A D^{-\frac{1}{2}}\right) X E_{\mathcal{G}} W_{\mathcal{G}}+E_{\mathcal{G}} b_{\mathcal{G}} Z=(IN​+D−21​AD−21​)XEG​WG​+EG​bG​

• 数据自适应图生成(DAGG)模块

第一次见到这么简单的自学习公式，特点是矩阵和自己的转置相乘可以直接得到一个对称矩阵，不过其他论文有时候假设的是具有非对称性

D − 1 2 A D − 1 2 = softmax ⁡ ( ReL ⁡ U ( E A ⋅ E A T ) ) \boldsymbol{D}^{-\frac{1}{2}} \boldsymbol{A} \boldsymbol{D}^{-\frac{1}{2}}=\operatorname{softmax}\left(\operatorname{ReL} U\left(\boldsymbol{E}_{\boldsymbol{A}} \cdot \boldsymbol{E}_{\boldsymbol{A}}^{\boldsymbol{T}}\right)\right) D−21​AD−21​=softmax(ReLU(EA​⋅EAT​))

• 自适应图卷积递归网络(AGCRN)

重写GRU计算过程

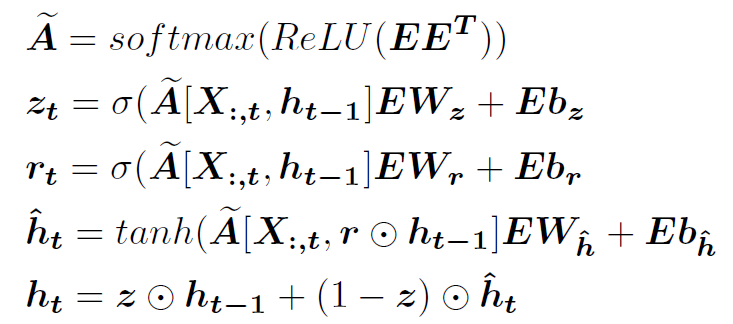
实验部分

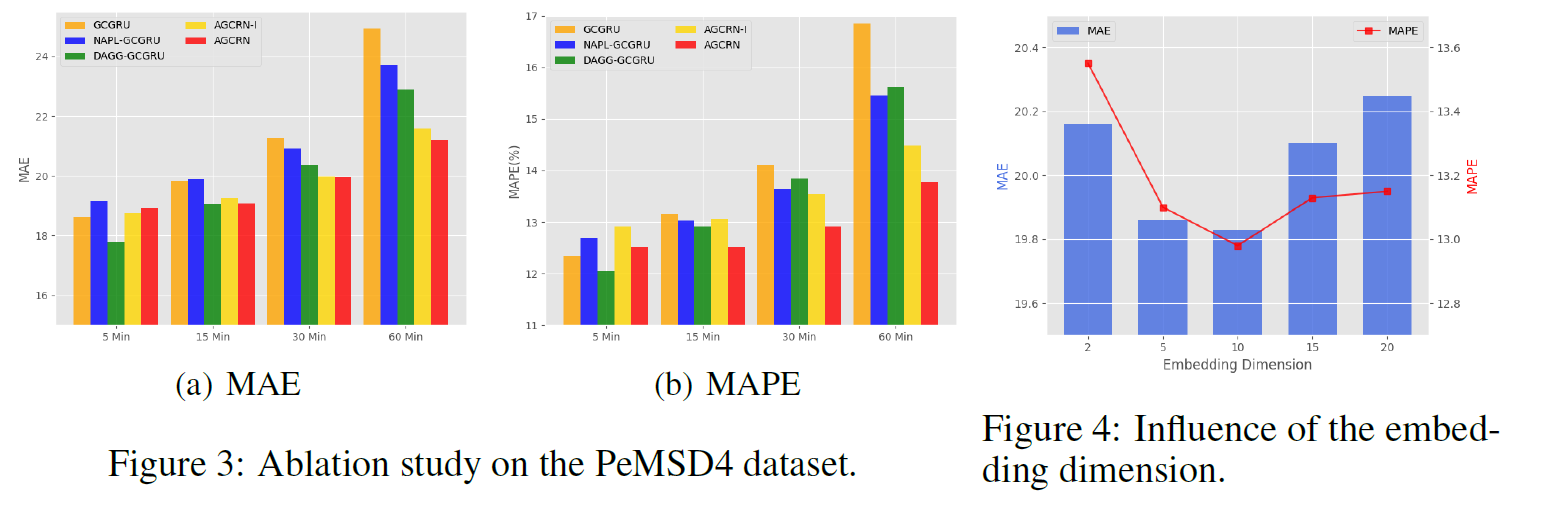
• 对比实验

• 消融实验

评价

这篇论文设计的比较巧妙的地方在于对传统图卷积的共享参数部分做了矩阵分解，从而获得节点特异性的参数。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！