用于交通预测的自适应图卷积递归网络
交通预测最近的工作主要集中在设计复杂的图神经网络结构，借助预定义的图来捕获共享模式。本文认为学习特定于节点的模式对于交通预测至关重要，而预定义的图是可以避免的。我们提出了两个自适应模块来增强图卷积网络（GCN）的新功能：1）节点自适应参数学习（NAPL）模块，捕获特定于节点的模式；2） 数据自适应图生成（DAGG）模块，用于自动推断不同交通序列之间的相互依赖关系。提出了一种自适应图卷积递归网络（AGCRN）。基于这两个模块和递归网络自动捕获交通序列中的细粒度空间和时间相关性。
传统方法只是应用时间序列模型，无法捕捉非线性相关性或复杂的时空模式。基于深度学习的方法，专注于新的神经网络架构，以捕获所有交通序列共享的显著时空模式。使用递归神经网络或时间卷积模块建模时间依赖性，使用基于GCN的方法建模非结构化交通序列及其相互依赖关系。但它们偏向于所有交通序列之间突出和共享的模式。共享参数空间使得当前的方法在准确捕获细粒度数据源特定模式方面较差。事实上，交通序列表现出多样化的模式，不同数据源（节点/传感器）有不同属性。此外，现有的基于GCN的方法需要通过相似性或距离度量预先定义一个连接图，以捕获空间相关性。以这种方式生成的图形通常是直观的、不完整的，并且不是直接针对预测任务的。
没有设计更复杂的网络体系结构，而是通过修改现有方法（即GCN）的基本构造块来分别解决上述问题。具体来说，我们建议使用两个用于流量预测任务的自适应模块来增强GCN。1）节点自适应参数学习（NAPL）模块，用于学习每个交通序列的节点特定的模式，NAPL分解传统GCN中的参数，并根据节点嵌入从所有节点共享的权重池和偏差池生成节点特定参数；2）数据自适应图生成（DAGG）模块，用于从数据中推断节点嵌入（属性），并在训练期间生成图形。NAPL和DAGG是独立的。模块中的所有参数都可以以端到端的方式学习。们将NAPL和DAGG与递归网络相结合，提出了一种统一的流量预测模型——自适应图卷积递归网络（AGCRN）。AGCRN可以捕获交通序列中特定于节点的细粒度空间和时间相关性，将修改后的GCN中嵌入的节点与DAGG中的嵌入统一起来。
问题定义：多步交通预测问题
表示t时间步的N个源，找到一个函数F，根据过去的T步历史数据，来预测下一个τ步数据
节点自适应参数学习
GCN的卷积操作可表示如下
，
代表可学习权重和偏差，Θ和b是在所有节点上共享的。虽然共享参数可能有助于在许多问题中学习所有节点中最显著的模式，并且可以显著减少参数数量，但我们发现对于交通预测问题，它是次优的。由于各种因素，不同交通序列之间往往存在不同的模式。仅捕获所有节点之间的共享模式对于准确的交通预测是不够的，必须为每个节点保持一个唯一的参数空间来学习特定于节点的模式。
但为每个节点分配参数
参数量太大，且可能过度拟合。故我们使用节点自适应参数学习模块来加强传统GCN，其用到矩阵分解。不是学习，NAPL学习两个更小的参数矩阵：1） 节点嵌入矩阵
d是嵌入维度，d<
生成。对于某个节点i，其参数
根据节点嵌入
从大的共享权重池
提取，这个可以解释为从由所有交通序列中发现的一组候选模式中学习特定于节点的模式。同样的操作也可用于b。NAPL-GCN可表示为
数据自适应图生成
另一个问题是需要一个提前定义的邻接矩阵。现有的工作主要是利用距离函数或相似性度量来提前计算图：1）距离函数，它根据不同节点之间的地理距离定义图；2） 相似性函数，通过测量节点属性或交通序列本身的相似性来定义节点接近度。这些方法非常直观。预定义图不能包含关于空间依赖性的完整信息，并且与预测任务没有直接关系，这可能会导致相当大的偏差。
为此我们提出了一个数据自适应图生成（DAGG）模块来自动从数据中推断隐藏的相互依赖关系。首先随机初始化的可学习节点嵌入字典
，EA的每一行代表一个节点嵌入，de表示节点嵌入的维度。通过将
相乘，我们可以推断出每对节点之间的空间相关性：
利用softmax函数对自适应矩阵进行归一化处理。EA将自动更新，以学习不同交通序列之间的隐藏依赖，并获得图卷积的自适应矩阵
DAGG增强的GCN可以表述为
自适应图卷积递归网络
自适应图卷积递归网络（AGCRN），它集成了NAPL-GCN、DAGG和门控递归单元（GRU），以捕获交通序列中特定于节点的空间和时间相关性。AGCRN将GRU中的MLP层替换为我们的NAPL-GCN，以学习特定于节点的模式。还通过DAGG模块自动发现空间依赖关系
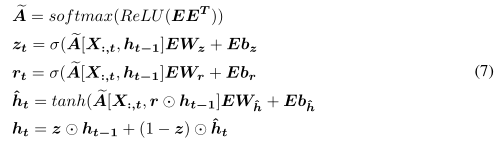
z和r分别是重置门和更新门。AGCRN中的所有参数都可以通过反向传播进行端到端的训练。AGCRN将所有嵌入矩阵统一为E，而不是在不同的NAPL-GCN层和DAGG中学习单独的节点嵌入矩阵。这提供了一个强大的正则化器，以确保所有GCN块中嵌入的节点一致，并使我们的模型具有更好的可解释性。
为了实现多步流量预测，我们将几个AGCRN层堆叠为编码器，以捕获特定于节点的时空模式。将历史数据表示为
。通过应用线性变换将表示从
投影到
，我们可以获得所有节点的接下来τ步的交通预测。我们选择L1损失作为我们的训练目标，并一起优化多步预测的损失。损失函数可以表示为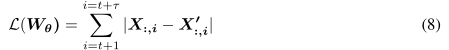
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！