矩阵论(五)——矩阵分析

矩阵论（五）——矩阵分析

• 1. 向量范数
• 2. 矩阵范数
• 3. 向量序列与矩阵序列的极限
• • 3.1 向量序列的极限
  • 3.2 矩阵序列的极限
• 4. 矩阵幂级数

1. 向量范数

向量范数： $\forall x\in V$，若非负实数$||x||$满足
   (1) 正定性：$||x||\ge 0，且||x||=0⟺x=0$
   (2) 齐次性：$||ax||=|a|||x||，a\in F$
   (3) 三角不等式：$\forall x，y\in V，都有||x+y||\le ||x||+||y||$
则称||x||为向量x的范数，$[V；||.||]$为赋范空间

1-范数： ∣ ∣ x ∣ ∣ 1 = Σ i ∣ x i ∣ ||x||_1 = \Sigma_i |x_i| ∣∣x∣∣1​=Σi​∣xi​∣
2-范数(向量长度，由内积所诱导的范数)： ∣ ∣ x ∣ ∣ 2 = ( x ， x ) = x H x = Σ i ∣ x i ∣ 2 ||x||_2 = \sqrt{(x，x)} = \sqrt{x^H x} = \sqrt{\Sigma_i|x_i|^2} ∣∣x∣∣2​=(x，x) ​=xHx ​=Σi​∣xi​∣2 ​
$\infty$-范数： ∣ ∣ x ∣ ∣ ∞ = m a x ∣ x i ∣ ||x||_\infty = max|x_i| ∣∣x∣∣∞​=max∣xi​∣
p-范数： ∀ p ∈ ( 1 , + ∞ ) ， ∣ ∣ x ∣ ∣ p = Σ i ∣ x i ∣ p p ， ∀ x ∈ C n \forall p \in (1,\ +\infty)，||x||_p = \sqrt[p]{\Sigma_i |x_i|^p}，\forall x \in C^n ∀p∈(1, +∞)，∣∣x∣∣p​=pΣi​∣xi​∣p ​，∀x∈Cn

例如：
若 x = ( 1 , i , 1 + i ) T x = (1,\ i,\ 1 + i)^T x=(1, i, 1+i)T，有
∣ ∣ x ∣ ∣ 1 = 1 + ∣ i ∣ + ∣ 1 + i ∣ = 1 + 1 + 2 = 2 + 2 ||x||_1 = 1 + |i| + |1 + i| = 1 + 1 + \sqrt{2} = 2 + \sqrt{2} ∣∣x∣∣1​=1+∣i∣+∣1+i∣=1+1+2 ​=2+2 ​
∣ ∣ x ∣ ∣ 2 = 1 2 + ∣ i ∣ 2 + ∣ 1 + i ∣ 2 = 1 + 1 + 2 2 = 2 ||x||_2 = \sqrt{1^2 + |i|^2 + |1 + i|^2} = \sqrt{1 + 1 + \sqrt{2}^2} = 2 ∣∣x∣∣2​=12+∣i∣2+∣1+i∣2 ​=1+1+2 ​2 ​=2
∣ ∣ x ∣ ∣ ∞ = m a x { 1 , 1 , 2 } = 2 ||x||_\infty = max\{1,\ 1,\ \sqrt{2}\} = \sqrt{2} ∣∣x∣∣∞​=max{1, 1, 2 ​}=2 ​


向量范数的连续性： α 1 , ⋯ , α n 为 C n \alpha_1,\ \cdots,\ \alpha_n为C^n α1​, ⋯, αn​为Cn的任一组基， ∣ ∣ . ∣ ∣ 为 C n ||.||为C^n ∣∣.∣∣为Cn上任一向量范数， ∀ x ∈ C n ， 有 x = Σ i x i α i ， x i ∈ C n ， 则 f ( x 1 , ⋯ , x n ) = ∣ ∣ x ∣ ∣ 为 x 1 , ⋯ , x n \forall x \in C^n，有x= \Sigma_i \ x_i \ \alpha_i，x_i \in C^n，则f(x_1,\ \cdots,\ x_n) = ||x||为x_1,\ \cdots,\ x_n ∀x∈Cn，有x=Σi​ xi​ αi​，xi​∈Cn，则f(x1​, ⋯, xn​)=∣∣x∣∣为x1​, ⋯, xn​的连续函数

向量范数的等价性： ∣ ∣ x ∣ ∣ ( 1 ) 与 ∣ ∣ x ∣ ∣ ( 2 ) ||x||^{(1)}与||x||^{(2)} ∣∣x∣∣(1)与∣∣x∣∣(2)是线性空间V上定义的两种向量范数，
若 ∃ c 1 , c 2 > 0 ， 使 c 1 ∣ ∣ x ∣ ∣ ( 2 ) ≤ ∣ ∣ x ∣ ∣ ( 1 ) ≤ c 2 ∣ ∣ x ∣ ∣ ( 2 ) ， ∀ x ∈ V \exists c_1, c_2 > 0，使c_1 ||x||^{(2)} \leq ||x||^{(1)} \leq c_2 ||x||^{(2)}，\forall x \in V ∃c1​,c2​>0，使c1​∣∣x∣∣(2)≤∣∣x∣∣(1)≤c2​∣∣x∣∣(2)，∀x∈V，则称这两个范数等价
有限维线性空间的任意两种向量范数都是等价的
在无限维线性空间中，两个向量范数是可以不等价的

2. 矩阵范数

矩阵范数： ∀ A ∈ F n × n \forall A \in F^{n \times n} ∀A∈Fn×n，对应一个非负实数||A||满足
  (1) 正定性：$||A||\ge 0，且||A||=0⟺A=0$
  (2) 齐次性：$||aA||=|a|||A||，a\in F$
  (3) 三角不等式： ∀ A ， B ∈ F n × n ， 都 有 ∣ ∣ A + B ∣ ∣ ≤ ∣ ∣ A ∣ ∣ + ∣ ∣ B ∣ ∣ \forall A，B \in F^{n \times n}，都有||A + B|| \leq ||A|| + ||B|| ∀A，B∈Fn×n，都有∣∣A+B∣∣≤∣∣A∣∣+∣∣B∣∣
  (4) 相容性： ∀ A ， B ∈ F n × n ， 都 有 ∣ ∣ A B ∣ ∣ ≤ ∣ ∣ A ∣ ∣ ∣ ∣ B ∣ ∣ \forall A，B \in F^{n \times n}，都有||AB|| \leq ||A|| \ ||B|| ∀A，B∈Fn×n，都有∣∣AB∣∣≤∣∣A∣∣ ∣∣B∣∣
则称||A||为矩阵A的范数

F(Frobenius)-范数： ∣ ∣ A ∣ ∣ F = Σ i Σ j ∣ a i j ∣ 2 ) = t r ( A H A ) = Σ i σ i 2 ||A||_F = \sqrt{\Sigma_{i} \Sigma_{j} |a_{ij}|^2)} = \sqrt{tr(A^HA)} = \sqrt{\Sigma_i \sigma_i^2} ∣∣A∣∣F​=Σi​Σj​∣aij​∣2) ​=tr(AHA) ​=Σi​σi2​ ​

例如：

A = ( a i j ) ∈ C n × n ， ∣ ∣ A ∣ ∣ F = Σ i Σ j ∣ a i j ∣ 2 A = (a_{ij}) \in C^{n \times n}，||A||_F = \sqrt{\Sigma_i \Sigma_j |a_{ij}|^2} A=(aij​)∈Cn×n，∣∣A∣∣F​=Σi​Σj​∣aij​∣2 ​，则
( 1 ) ∣ ∣ A ∣ ∣ F = ∣ ∣ A H ∣ ∣ F (1) \quad ||A||_F = ||A^H||_F (1)∣∣A∣∣F​=∣∣AH∣∣F​
( 2 ) ∣ ∣ U A ∣ ∣ F = ∣ ∣ A V ∣ ∣ F = ∣ ∣ U A V ∣ ∣ F = ∣ ∣ A ∣ ∣ F (2) \quad ||UA||_F = ||AV||_F = ||UAV||_F = ||A||_F (2)∣∣UA∣∣F​=∣∣AV∣∣F​=∣∣UAV∣∣F​=∣∣A∣∣F​，其中U，V是酉矩阵
( 3 ) t r ( A H A ) = Σ i Σ j ∣ a i j ∣ 2 (3) \quad tr(A^H A) = \Sigma_i \Sigma_j |a_{ij}|^2 (3)tr(AHA)=Σi​Σj​∣aij​∣2

例如：
A = ( 0 3 i 1 0 − 1 0 − 1 1 2 ) ， A H A = ( 1 − 1 2 − 1 11 2 − 3 i − 2 2 + 3 i 5 ) A = \begin{pmatrix} 0 & 3i & 1 \\ 0 & -1 & 0 \\ -1 & 1 & 2 \end{pmatrix}，A^HA = \begin{pmatrix} 1 & -1 & 2 \\ -1 & 11 & 2-3i \\ -2 & 2 + 3i & 5 \end{pmatrix} A=⎝⎛​00−1​3i−11​102​⎠⎞​，AHA=⎝⎛​1−1−2​−1112+3i​22−3i5​⎠⎞​
∣ ∣ A ∣ ∣ F = 9 + 1 + 1 + 1 + 1 + 4 = t r ( A H A ) = 1 + 11 + 5 = 17 ||A||_F = \sqrt{9 + 1 + 1 + 1 + 1 + 4} = \sqrt{tr(A^HA)} = \sqrt{1 + 11 + 5} = \sqrt{17} ∣∣A∣∣F​=9+1+1+1+1+4 ​=tr(AHA) ​=1+11+5 ​=17 ​

相容范数： $||Ax||\le ||A||.||x||$，其中||x||是向量范数，||A||是矩阵范数

诱导范数： ∣ ∣ A ∣ ∣ = m a x { ∣ ∣ A x ∣ ∣ ∣ ∣ x ∣ ∣ } ||A|| = max\{\frac{||Ax||}{||x||}\} ∣∣A∣∣=max{∣∣x∣∣∣∣Ax∣∣​}，其中||x||是向量范数且$x\ne 0$，称||A||为由向量范数||x||所诱导的诱导范数

矩阵p-范数： 由 ∣ ∣ x ∣ ∣ p ||x||_p ∣∣x∣∣p​所诱导的矩阵范数。常用的p-范数为 ∣ ∣ A ∣ ∣ 1 ， ∣ ∣ A ∣ ∣ 2 与 ∣ ∣ A ∣ ∣ ∞ ||A||_1，||A||_2与||A||_\infty ∣∣A∣∣1​，∣∣A∣∣2​与∣∣A∣∣∞​

列和范数： ∣ ∣ A ∣ ∣ 1 = m a x ( Σ i = 1 n ∣ a i j ∣ ) ||A||_1 = max(\Sigma_{i = 1}^n |a_{ij}|) ∣∣A∣∣1​=max(Σi=1n​∣aij​∣)，np.max(np.sum(abs(arr), axis=1, keepdims=True), axis=0)

行和范数： ∣ ∣ A ∣ ∣ ∞ = m a x ( Σ j = 1 n ∣ a i j ∣ ) ||A||_\infty = max(\Sigma_{j = 1}^n |a_{ij}|) ∣∣A∣∣∞​=max(Σj=1n​∣aij​∣)，np.max(np.sum(abs(arr), axis=0, keepdims=True), axis=1)

谱范数： ∣ ∣ A ∣ ∣ 2 = λ 1 ， λ 1 是 A H A ||A||_2 = \sqrt{\lambda_1}，\lambda_1是A^HA ∣∣A∣∣2​=λ1​ ​，λ1​是AHA的最大特征值

例如：

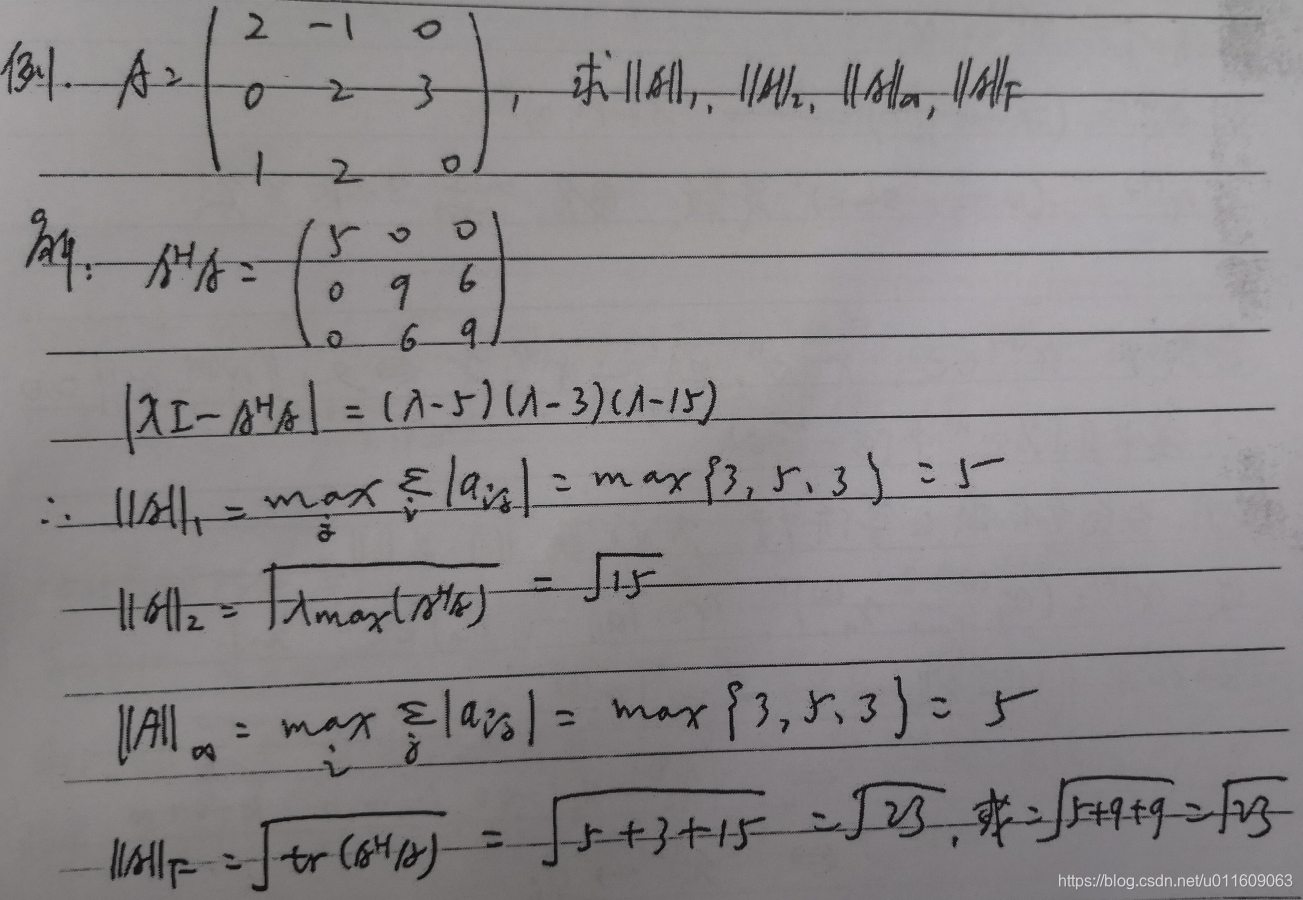
3. 向量序列与矩阵序列的极限

3.1 向量序列的极限

x ( k ) = ( x 1 ( k ) ⋯ x n ( k ) ) T ， k = 1 ， 2 ， ⋯ 是 C n x^{(k)} = (x_1^{(k)} \quad \cdots \quad x_n^{(k)})^T，k = 1，2，\cdots是C^n x(k)=(x1(k)​⋯xn(k)​)T，k=1，2，⋯是Cn空间的一个向量序列，如果当$k\to +\infty$时，它的n个分量数列都收敛，即 lim ⁡ k → ∞ x i ( k ) = a i ， i = 1 ， 2 ， ⋯ ， n \lim_{k \to \infty} x_i^{(k)} = a_i，i = 1，2，\cdots，n limk→∞​xi(k)​=ai​，i=1，2，⋯，n，则称向量序列 { x ( k ) } \{x^{(k)}\} {x(k)}是按分量收敛的。向量 α = ( α 1 ⋯ α n ) T \alpha = (\alpha_1 \quad \cdots \quad \alpha_n)^T α=(α1​⋯αn​)T是它的极限，记为 l i m k → ∞ x ( k ) = α 或 x ( k ) → α lim_{k \rightarrow \infty} x^{(k)} = \alpha或 x^{(k)} \rightarrow \alpha limk→∞​x(k)=α或x(k)→α
当至少有一个分量数列是发散的，则称向量序列是发散的。
例如

x ( k ) ∈ C n ， α ∈ C n ， 则 lim ⁡ k → ∞ x ( k ) = α ⟺ lim ⁡ k → ∞ ∣ ∣ x ( k ) − α ∣ ∣ = 0 x^{(k)} \in C^n，\alpha \in C^n，则\lim_{k \rightarrow \infty}x^{(k)} = \alpha \iff \lim_{k \rightarrow \infty} ||x^{(k)} - \alpha|| = 0 x(k)∈Cn，α∈Cn，则limk→∞​x(k)=α⟺limk→∞​∣∣x(k)−α∣∣=0，其中 ∣ ∣ . ∣ ∣ 为 C n ||.||为C^n ∣∣.∣∣为Cn中任一范数

3.2 矩阵序列的极限

矩阵序列 { A ( k ) } ， A ( k ) = ( a i j ( k ) ) ∈ C n × n ， 若 lim ⁡ k → ∞ a i j ( k ) = a i j ， i ， j = 1 ， ⋯ ， n \{A^{(k)}\}，A^{(k)} = (a_{ij}^{(k)}) \in C^{n \times n}，若\lim_{k \rightarrow \infty} a_{ij}^{(k)} = a_{ij}，i，j = 1，\cdots，n {A(k)}，A(k)=(aij(k)​)∈Cn×n，若limk→∞​aij(k)​=aij​，i，j=1，⋯，n，
则称矩阵序列 { A ( k ) } \{A^{(k)}\} {A(k)}收敛， A = ( a i j ( k ) ) 称 为 { A ( k ) } A = (a_{ij}^{(k)})称为\{A^{(k)}\} A=(aij(k)​)称为{A(k)}的极限，记为 lim ⁡ k → ∞ A ( k ) = A 或 A ( k ) = A ， k → ∞ \lim_{k \rightarrow \infty}A^{(k)} = A或A^{(k)} = A，k \rightarrow \infty limk→∞​A(k)=A或A(k)=A，k→∞
例如：
A ( k ) = ( ( ( 1 + 1 k ) k 1 + 1 k − 1 ( − 1 ) k k ) ⟶ A = ( e 1 − 1 0 ) A^{(k)} = \begin{pmatrix} ((1 + \frac{1}{k}) ^ k & 1 + \frac{1}{k} \\ \\ -1 & \frac{(-1)^k}{k} \end{pmatrix} \longrightarrow A = \begin{pmatrix} e & 1 \\ \\ -1 & 0 \end{pmatrix} A(k)=⎝⎛​((1+k1​)k−1​1+k1​k(−1)k​​⎠⎞​⟶A=⎝⎛​e−1​10​⎠⎞​

{ A ( k ) } ∈ C n × n ， ∣ ∣ A ∣ ∣ ∈ C n × n ， 则 l i m k → ∞ A ( k ) = ∣ ∣ A ∣ ∣ ⟺ l i m k → ∞ ∣ ∣ A ( k ) − A ∣ ∣ = 0 \{A^{(k)}\} \in C^{n \times n}，||A|| \in C^{n \times n}，则lim_{k \rightarrow \infty} A^{(k)} = ||A|| \iff lim_{k \rightarrow \infty} ||A^{(k)} - A|| = 0 {A(k)}∈Cn×n，∣∣A∣∣∈Cn×n，则limk→∞​A(k)=∣∣A∣∣⟺limk→∞​∣∣A(k)−A∣∣=0，其中 ∣ ∣ . ∣ ∣ 为 C n ||.||为C^n ∣∣.∣∣为Cn中任一范数

4. 矩阵幂级数

谱半径： ρ ( A ) = m a x ( ∣ λ i ∣ ) ， λ i ∈ { λ 1 , λ 2 , ⋯ , λ n } ， { λ 1 , λ 2 , ⋯ , λ n } 矩 阵 A ∈ C n × n \rho(A) = max(|\lambda_i|)，\lambda_i \in \{\lambda_1,\ \lambda_2,\ \cdots,\ \lambda_n\}，\{\lambda_1,\ \lambda_2,\ \cdots,\ \lambda_n\}矩阵A \in C^{n \times n} ρ(A)=max(∣λi​∣)，λi​∈{λ1​, λ2​, ⋯, λn​}，{λ1​, λ2​, ⋯, λn​}矩阵A∈Cn×n的全部特征值

ρ ( A k ) = ( ρ ( A ) ) k \rho(A^k) = (\rho(A))^k ρ(Ak)=(ρ(A))k
A k → 0 ( k → ∞ ) ⟺ ρ ( A ) < 1 A^k \rightarrow 0(k \rightarrow \infty) \iff \rho(A) < 1 Ak→0(k→∞)⟺ρ(A)<1

A ∈ C n × n ， ∀ 矩 阵 范 数 ∣ ∣ A ∣ ∣ ∈ C n × n ， 都 有 ρ ( A ) ≤ ∣ ∣ A ∣ ∣ A \in C^{n \times n}，\forall 矩阵范数||A|| \in C^{n \times n}，都有\rho(A) \leq ||A|| A∈Cn×n，∀矩阵范数∣∣A∣∣∈Cn×n，都有ρ(A)≤∣∣A∣∣。即A的谱半径是A的任意一种矩阵范数的下界。

A ∈ C n × n ， ∀ ϵ > 0 A \in C^{n \times n}，\forall \epsilon > 0 A∈Cn×n，∀ϵ>0，存在某种矩阵范数 ∣ ∣ A ∣ ∣ ∗ ， 使 ∣ ∣ A ∣ ∣ ∗ ≤ ρ ( A ) + ϵ ||A||_*，使||A||_* \leq \rho(A) + \epsilon ∣∣A∣∣∗​，使∣∣A∣∣∗​≤ρ(A)+ϵ。即A的谱半径是A的所有矩阵范数的下确界
证明：

矩阵幂级数： Σ k = 0 ∞ a k A k = a 0 I + a 1 A + ⋯ + a k A k + ⋯ ， 其 中 A ∈ C n × n ， a k ∈ C \Sigma_{k = 0}^{\infty} a_k A^k = a_0 I + a_1 A + \cdots + a_k A^k + \cdots，其中A \in C^{n \times n}，a_k \in C Σk=0∞​ak​Ak=a0​I+a1​A+⋯+ak​Ak+⋯，其中A∈Cn×n，ak​∈C

矩阵幂级数的部分和： S n ( A ) = Σ k = 0 n a k A k S_n(A) = \Sigma^n_{k = 0} a_k A^k Sn​(A)=Σk=0n​ak​Ak

若 { S n ( A ) } \{S_n(A)\} {Sn​(A)}收敛，则称 Σ k = 0 ∞ a k A k \Sigma^\infty_{k = 0}a_kA^k Σk=0∞​ak​Ak收敛，否则发散

若 lim ⁡ n → ∞ S n ( A ) = S \lim_{n \rightarrow \infty} S_n(A) = S limn→∞​Sn​(A)=S，则称S为 Σ k = 0 ∞ a k A k \Sigma_{k = 0}^\infty a_kA^k Σk=0∞​ak​Ak的和矩阵

收敛性判别： 若复变量z的幂级数 Σ k = 0 ∞ a k z k \Sigma_{k = 0}^{\infty}a_k z^k Σk=0∞​ak​zk的收敛半径为R， R = lim ⁡ n → ∞ a n a n + 1 R = \lim_{n \to \infty} \frac{a_n}{a_{n + 1}} R=limn→∞​an+1​an​​，而方阵 A ∈ C n × n A \in C^{n \times n} A∈Cn×n的谱半径为$\rho (A)$，则
  (1) ρ ( A ) < R ， 则 Σ k = 0 ∞ a k A k \rho(A) < R，则\Sigma_{k = 0}^\infty a_k A^k ρ(A)<R，则Σk=0∞​ak​Ak收敛
  (2) ρ ( A ) > R ， 则 Σ k = 0 ∞ a k A k \rho(A) > R，则\Sigma_{k = 0}^\infty a_k A^k ρ(A)>R，则Σk=0∞​ak​Ak发散
  (3) ρ ( A ) = R ， 则 Σ k = 0 ∞ a k A k \rho(A) = R，则\Sigma_{k = 0}^\infty a_k A^k ρ(A)=R，则Σk=0∞​ak​Ak收敛性不定

例如：

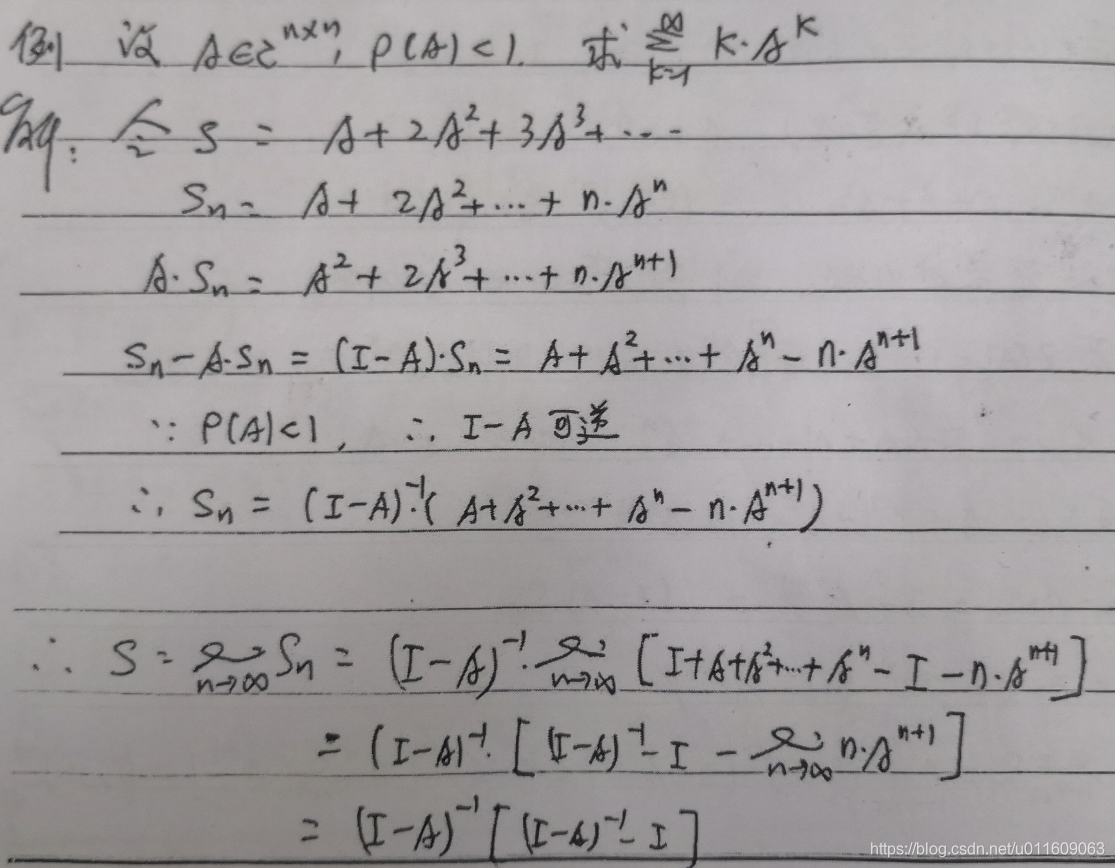
本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！