矩阵分析与计算学习记录-矩阵函数

本章重点内容：

矩阵函数的定义和计算

矩阵函数的导数和积分：导数定义和性质、对矩阵变量的导数、矩阵函数的积分及其性质

利用矩阵函数求解线性常系数微分方程：一阶线性常系数微分方程、n阶线性常系数微分方程

1. 矩阵函数的定义和计算

1.1 矩阵函数的定义

首先补充一下最小多项式的求法

 下面看一个例子

1.2 矩阵函数的计算

矩阵函数的计算分为四种方式：

• 利用Hamilton-Cayley定理计算矩阵函数
• 利用相似对角化计算矩阵函数
• 利用Jordan标准型计算矩阵函数
• 利用待定系数法求解矩阵函数
• 利用多项式表达求解矩阵函数

1.2.1 Jordan标准型计算矩阵函数

首先来看利用Jordan标准型计算矩阵函数 ，但是计算量比较大

 下面看到例题：

如果不清楚怎么求Joradn标准型和相似变换矩阵P的可以先看一下下面的网址

求矩阵的Jordan标准形和相应的相似变换矩阵

以上就是直接求出Jordan标准型的方法

 下面我们看如何利用Jordan标准型来解决矩阵函数的问题

 1.2.2  多项式表示求矩阵函数

利用多项式表示求矩阵函数相较于Jordan标准型，可以减少计算量，不需要求解和

 下面来看个例题

 1.2.3 待定系数法求矩阵函数

 下面我们来看如何利用待定系数法求解矩阵函数

 1.2.4 Hamilton-Cayley定理求解矩阵函数

 基本思想：找出矩阵方幂之间的关系，然后化简矩阵幂级数，求出矩阵函数的值。

1.2.5 相似变换矩阵求矩阵函数

 不知道怎么求解相似对角化矩阵的可以看一下

求解相似对角阵

1.2.6 矩阵函数的一些性质 

1.3 矩阵函数的幂级数表示

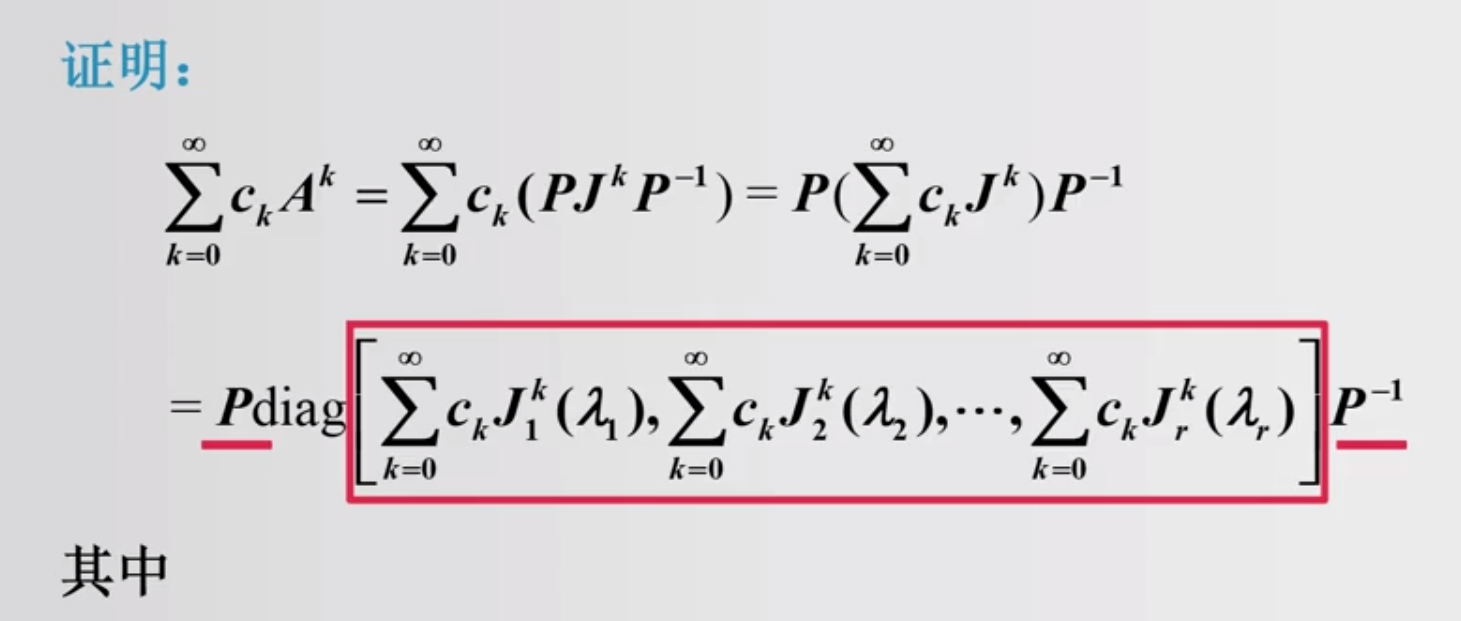
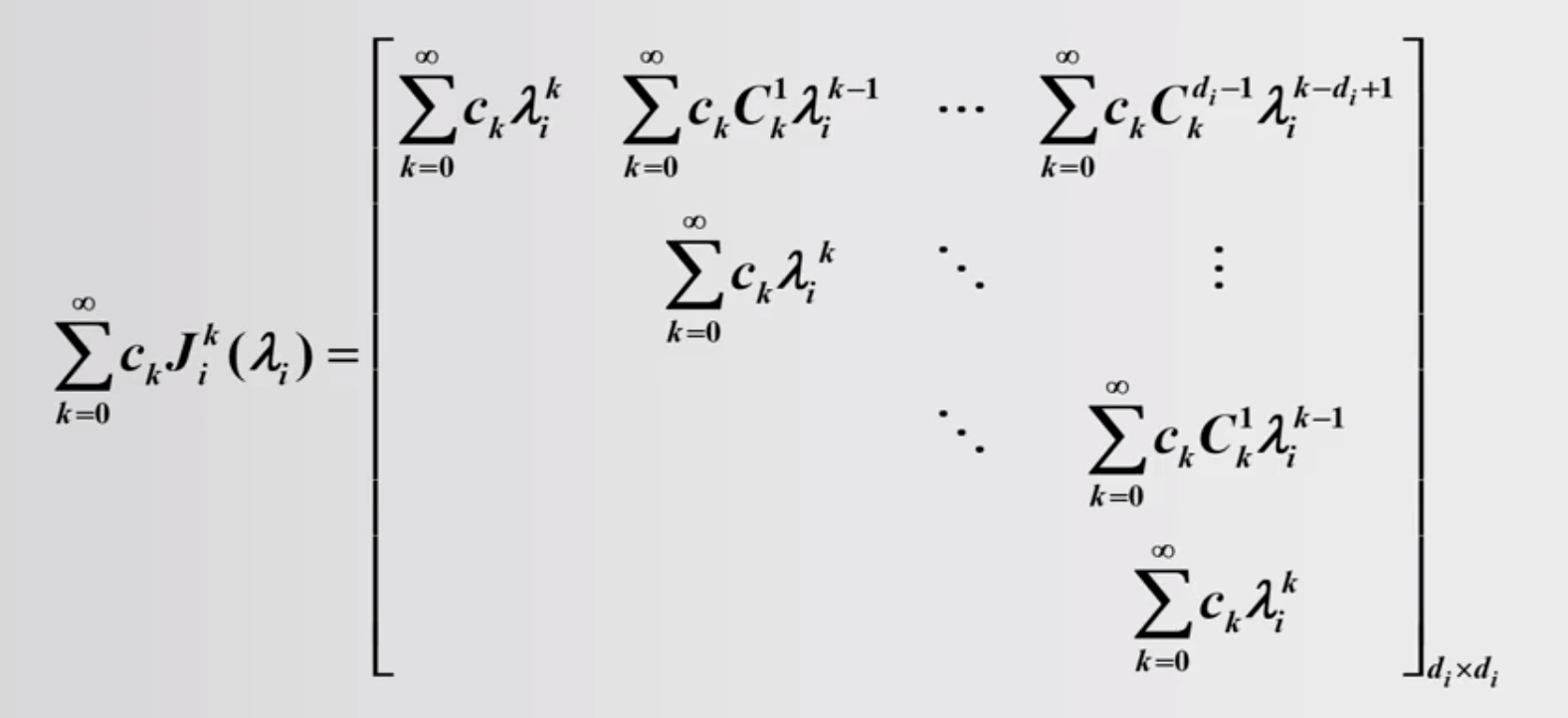
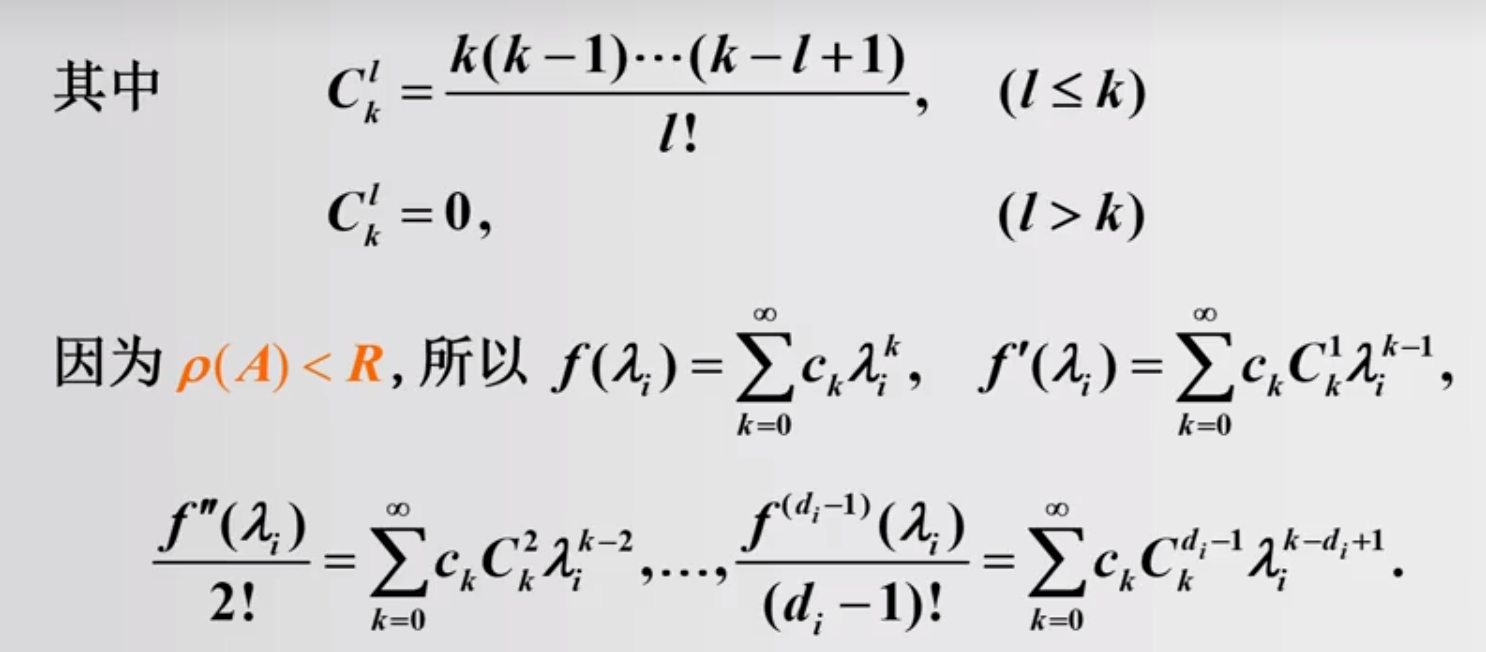
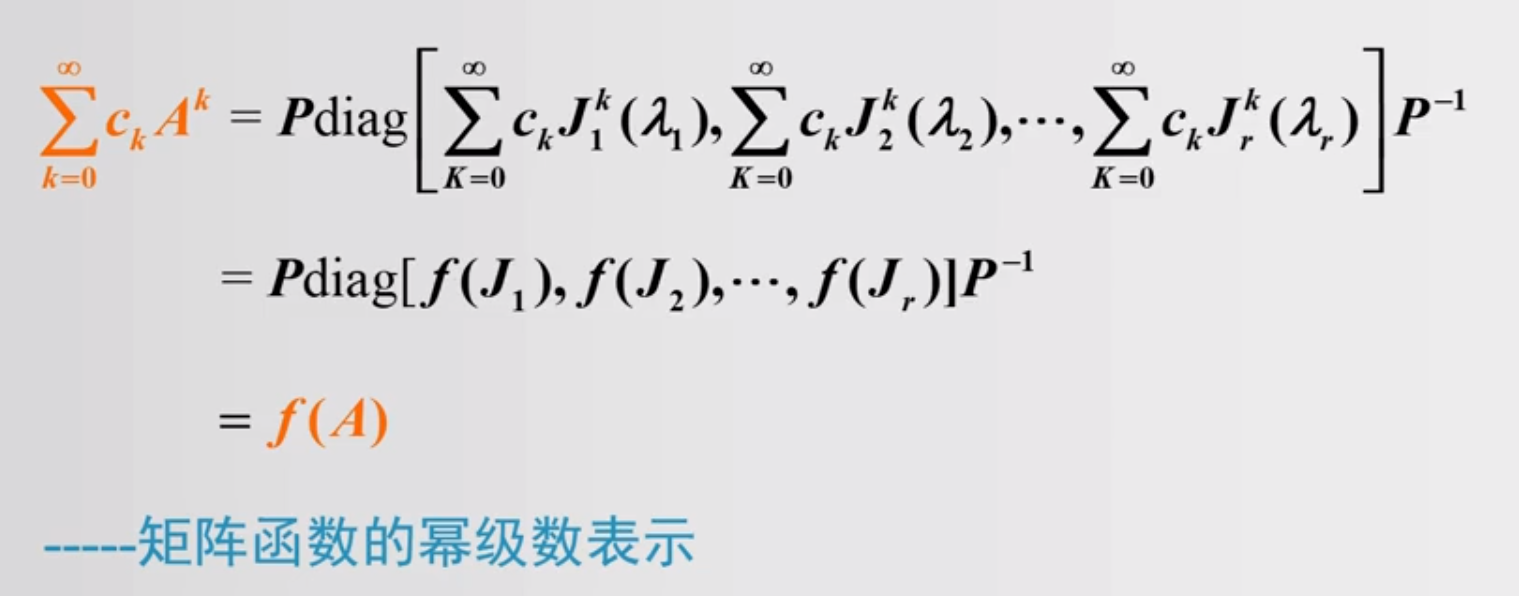
常用的幂级数展开

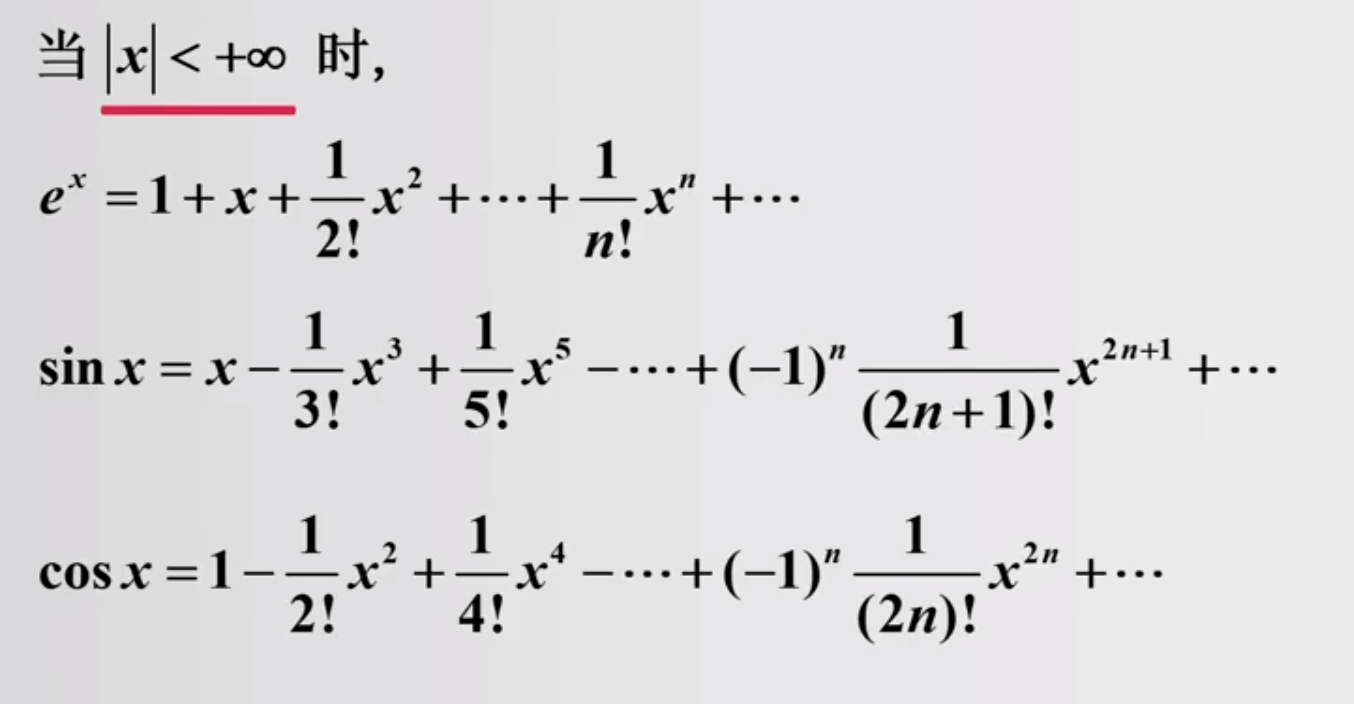
对应的矩阵函数

显而易见的是，我们不喜欢上图右侧的计算方式，计算一个 A2 的计算复杂度都是 n3 级别的尤其还有A的更高幂，为了节省计算资源和计算方便，使用Jordan分解来计算幂级数。

 下面我们看一道具体的例题

 特征变量都是2，所以谱半径为2

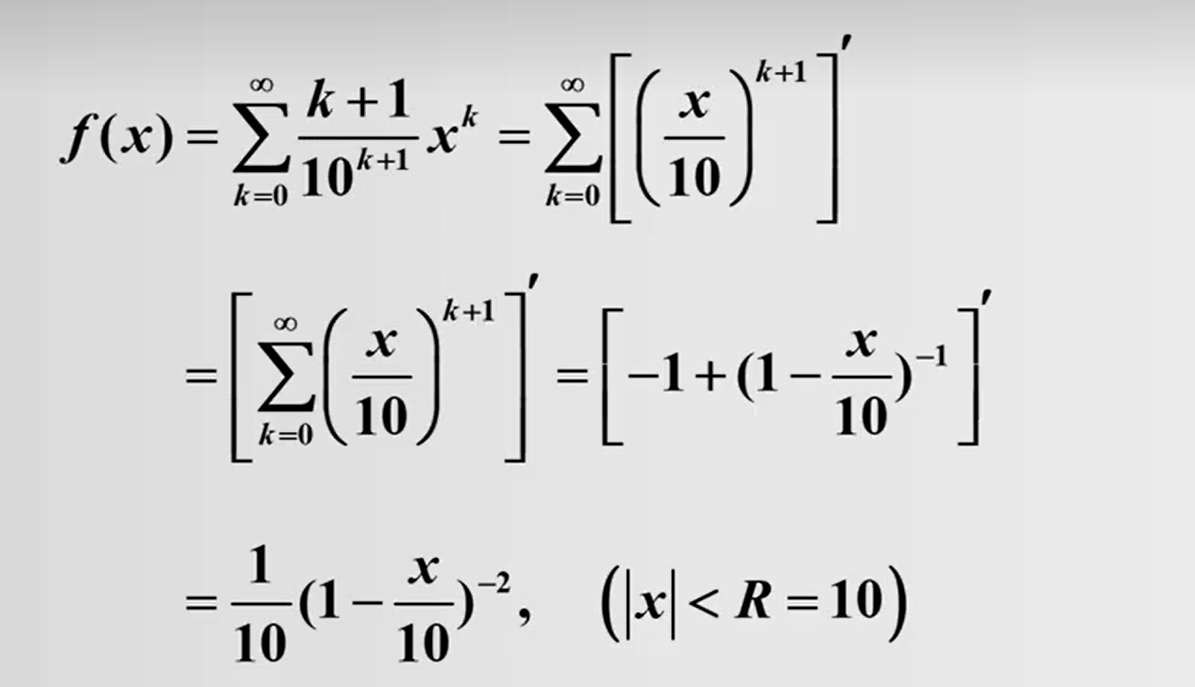
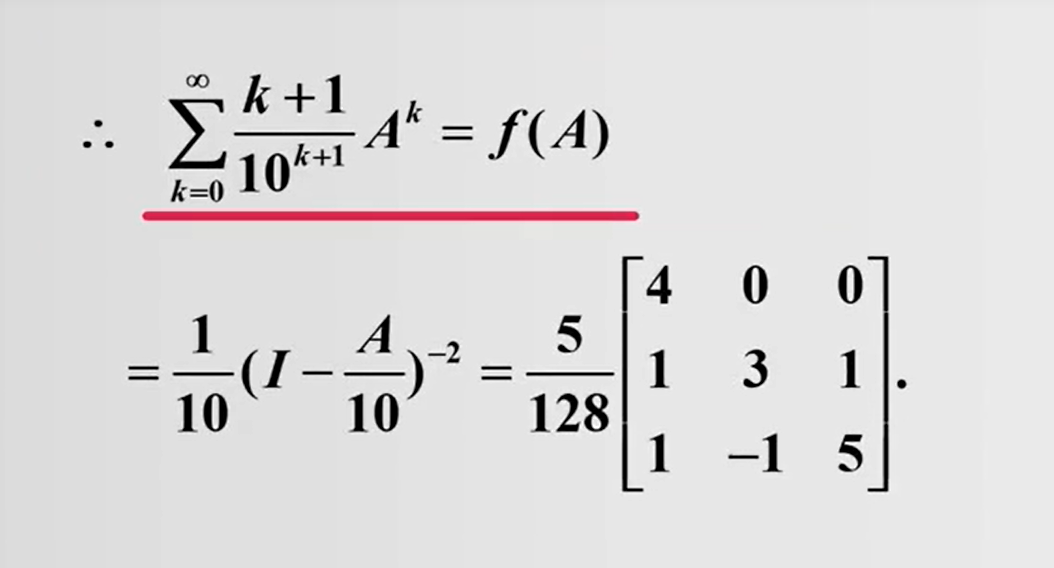
1.4 矩阵指数函数与矩阵三角函数

有如下的性质：

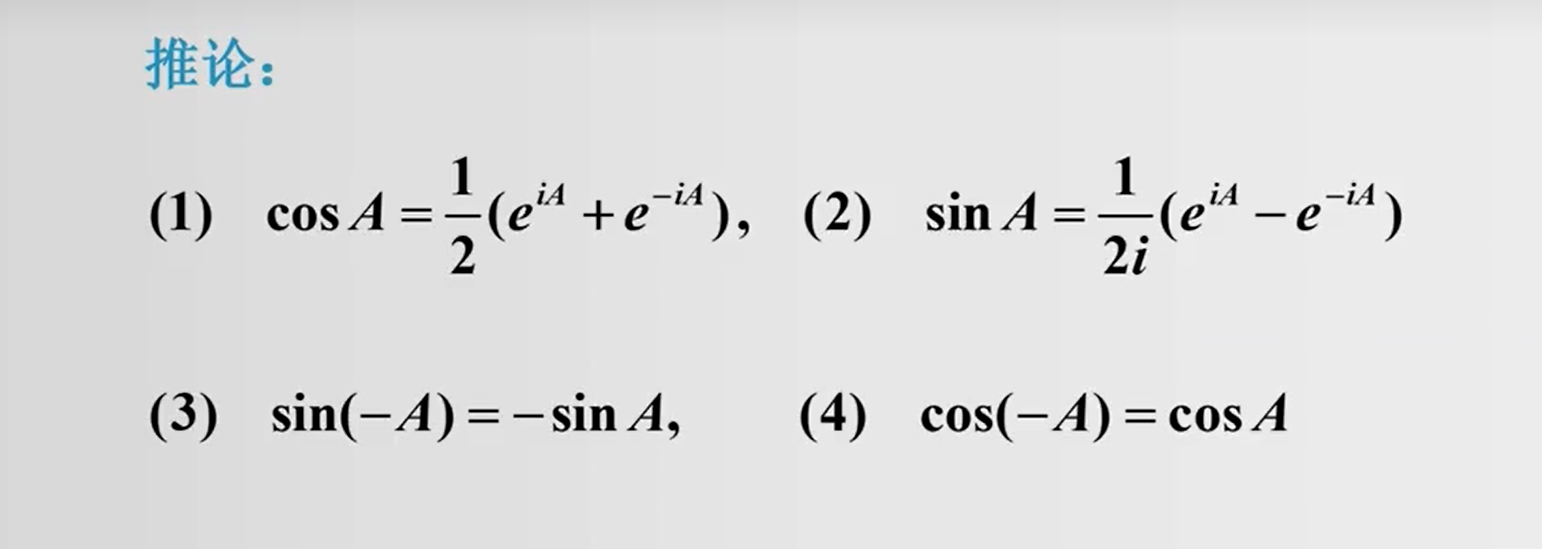
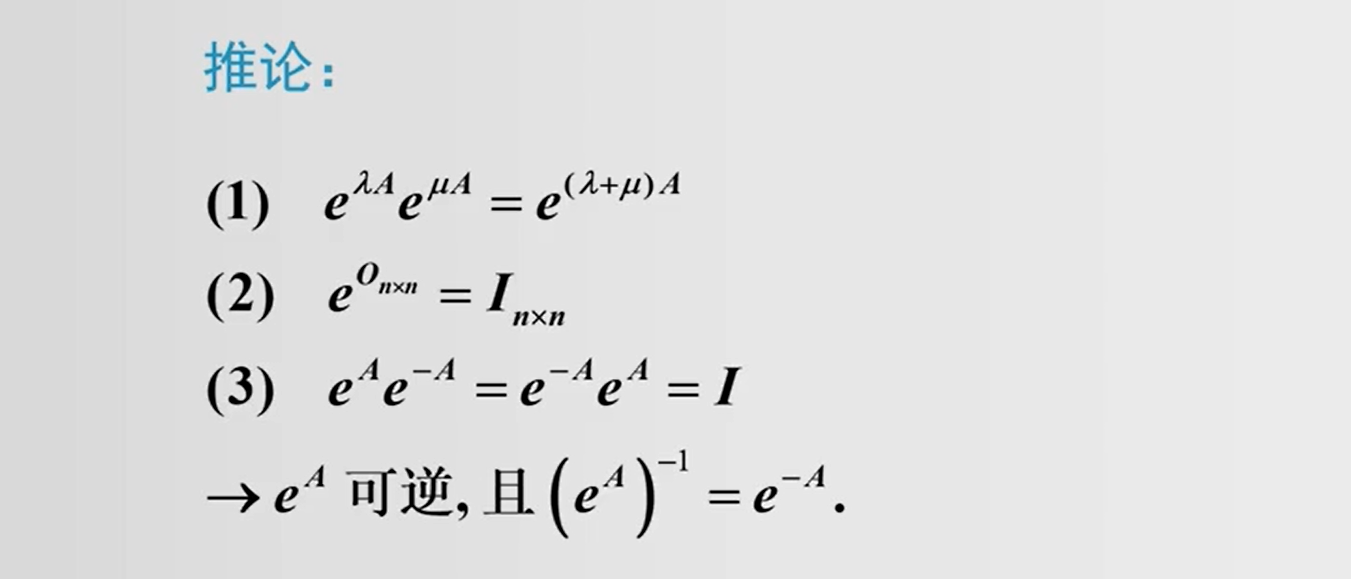
 下面看两个证明例题：

 
 2. 矩阵函数的导数和积分

 2.1 函数矩阵

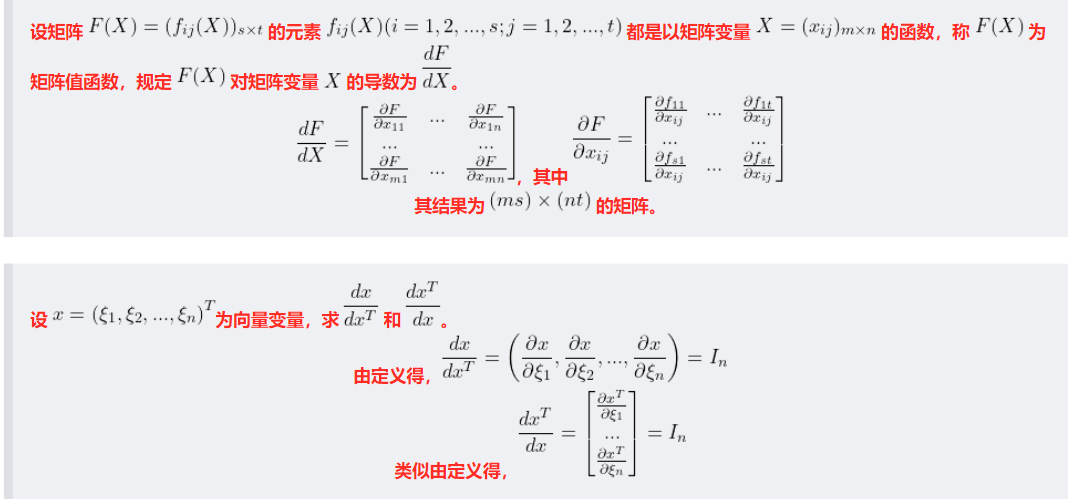
 2.2 矩阵函数的导数和积分

接下来我们看可导的定义：

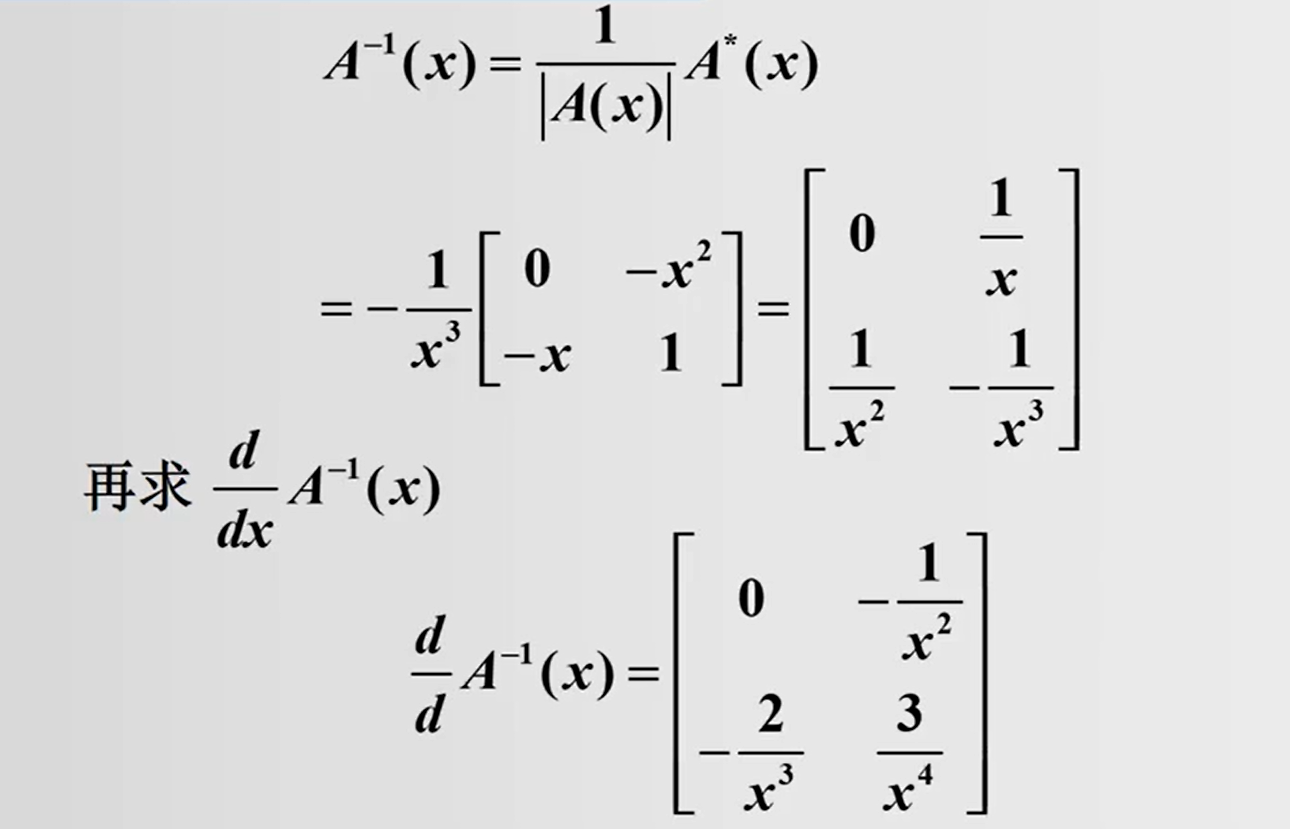
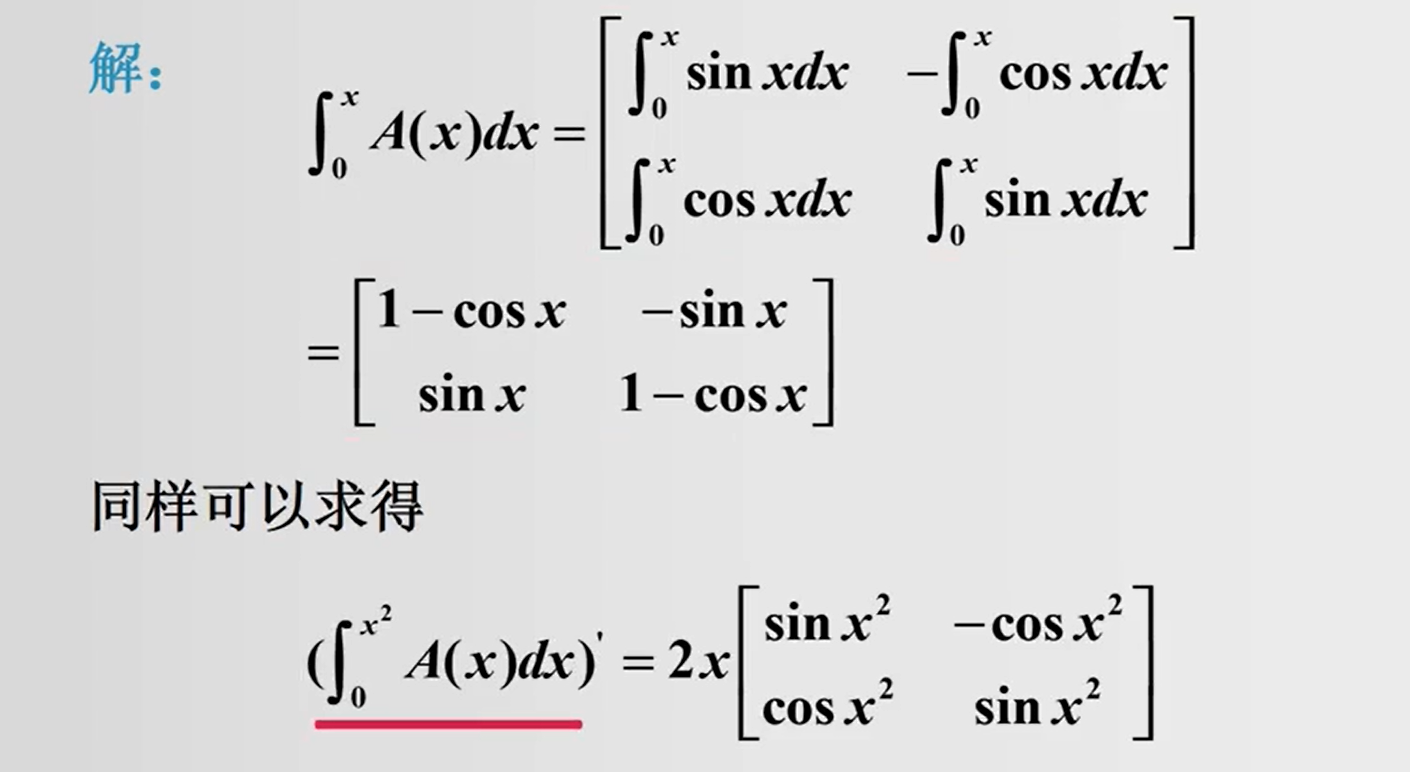
 函数向量的线性相关性：

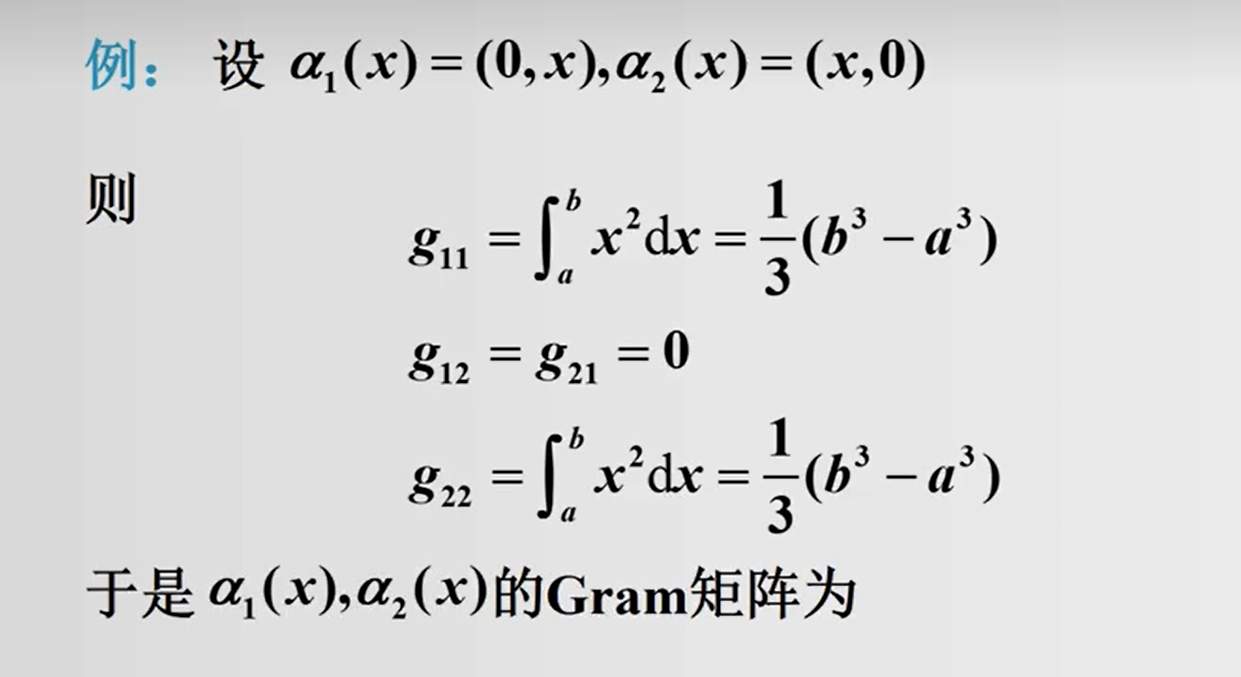
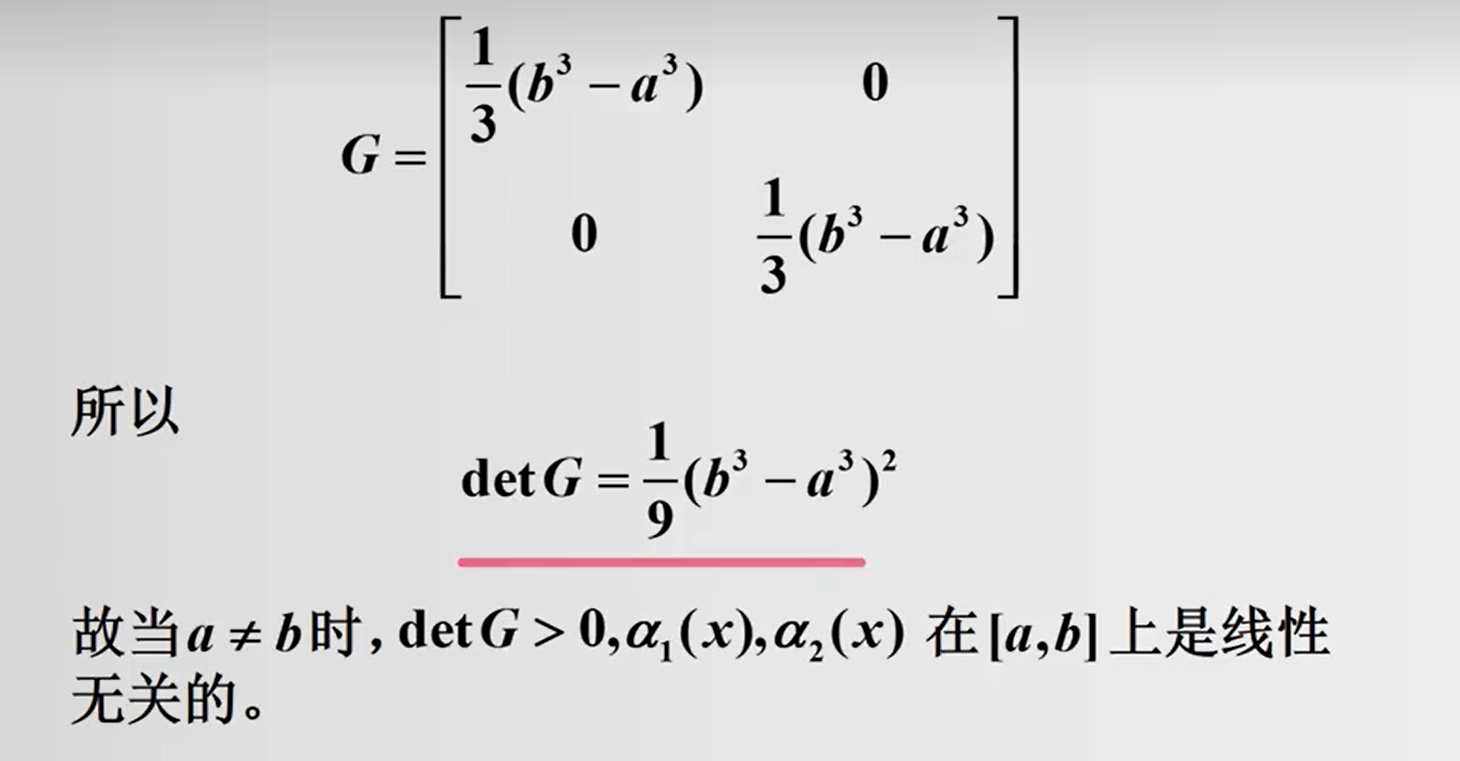
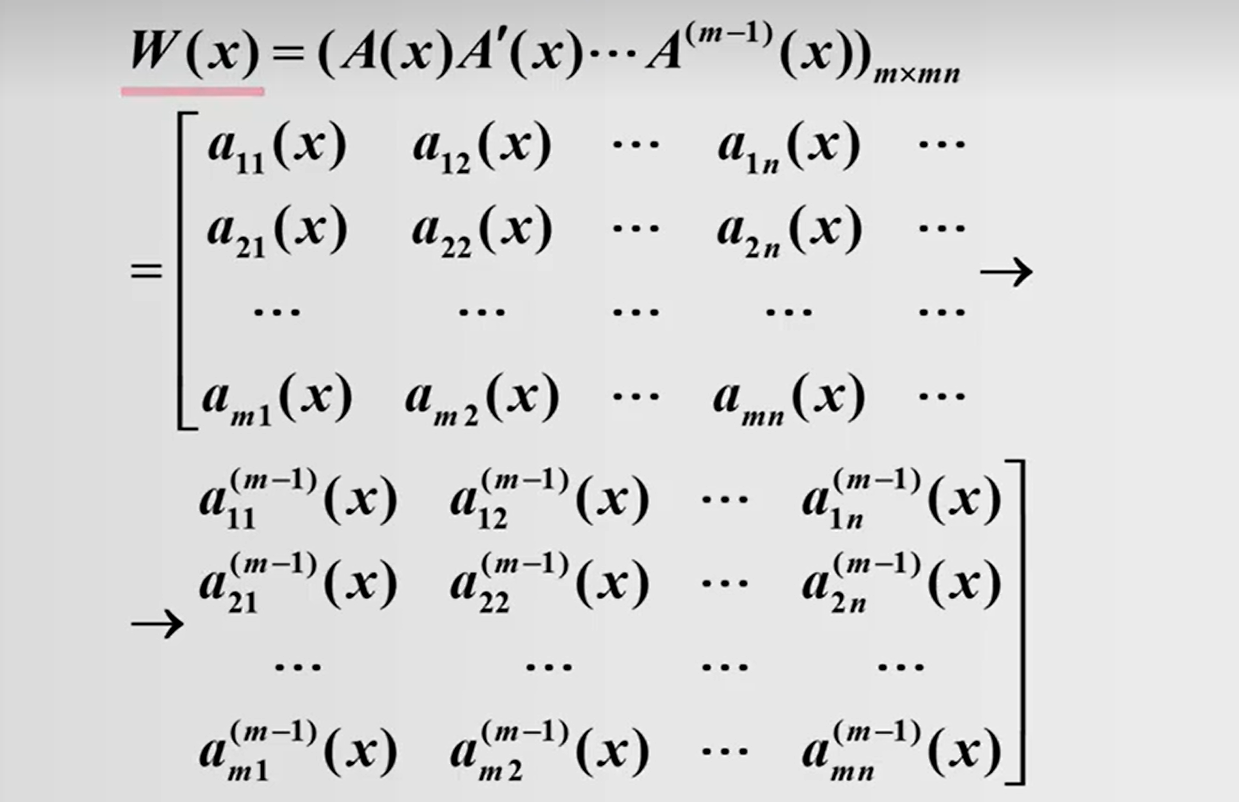
 对可导和积分的总结：

3.  利用矩阵函数求解线性常系数微分方程

 3.1 一阶常系数线性微分方程组

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！