试位法求取方程根

问题背景：本次我们来求取 f(x) = -2x^3 + 5x^2 + 9，这个函数，在给定区间[1.0, 3.9]上的零点。

解决方法：试位法

编程语言：python

说明：这里将分别使用两种编程语言和3种二分法的终止条件来完成试位的求解。

函数图像：

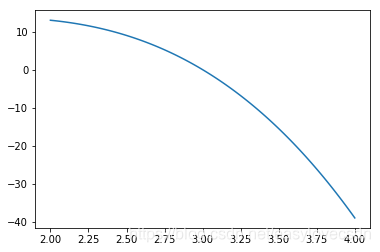
试位的终止条件：

1.区间小于某标准值

2.循环次数

3.真实误差小于某值 |(Xnew - Xold) / Xnew| * 100%

流程图：

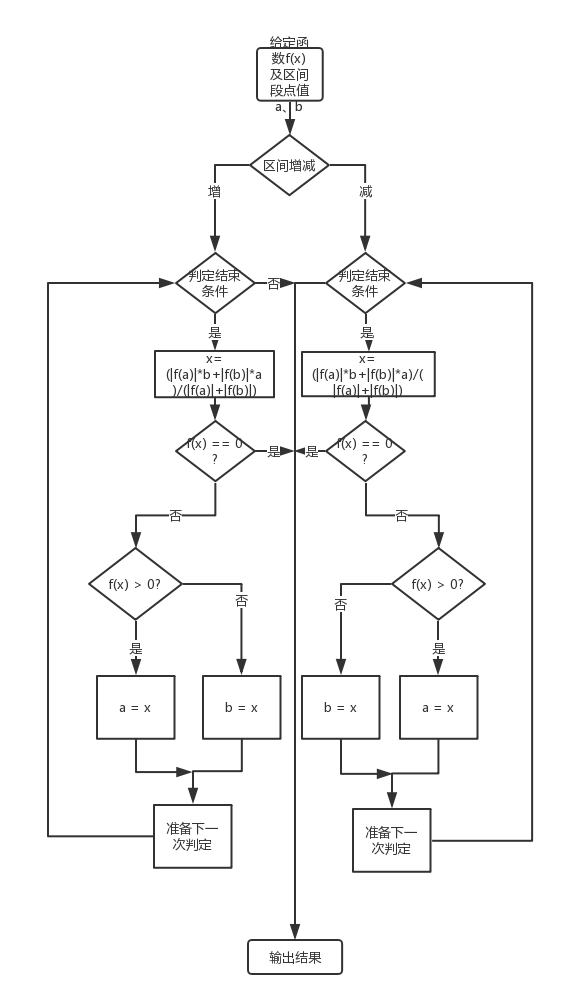
python代码

1.循环次数

# -*- coding: utf-8 -*-import math#最大循环次数
maxn = 9999#定义函数f(x)
def f(x):return -2.0 * x**3 + 5.0 * x**2 + 9.0#规定两区间端点
a = 1.0
b = 3.9#试位法寻求方程解
if (f(a) > 0) :for i in range(maxn) : fa = math.fabs(f(a))fb = math.fabs(f(b))x = (fa * b + fb * a) / (fa + fb)if (f(x) == 0) :breakif (f(x) > 0) :a = xelse :b = xelse :for i in range(maxn) :fa = math.fabs(f(a))fb = math.fabs(f(b))x = (fa * b + fb * a) / (fa + fb)if (f(x) == 0) :breakif (f(x) > 0) :b = xelse :a = x #输出结果       
print("f(%.3lf) = %.3lf\n" %(x, f(x)))

2. 区间长度

# -*- coding: utf-8 -*-import mathboard = 0.5#定义函数f(x)
def f(x):return -2.0 * x**3 + 5.0 * x**2 + 9.0#规定两区间端点
a = 1.0
b = 3.9#试位法寻求方程解
if (f(a) > 0) :while math.fabs(a - b) > board : fa = math.fabs(f(a))fb = math.fabs(f(b))x = (fa * b + fb * a) / (fa + fb)if (f(x) == 0) :breakif (f(x) > 0) :a = xelse :b = xelse :while math.fabs(a - b) > board :fa = math.fabs(f(a))fb = math.fabs(f(b))x = (fa * b + fb * a) / (fa + fb)if (f(x) == 0) :breakif (f(x) > 0) :b = xelse :a = x #输出结果       
print("f(%.3lf) = %.3lf\n" %(x, f(x)))

3.真实误差

# -*- coding: utf-8 -*-import mathrate = 0.000001#定义函数f(x)
def f(x):return -2.0 * x**3 + 5.0 * x**2 + 9.0#规定两区间端点
a = 1.0
b = 3.9err = 0x3f3f3f3f#试位法寻求方程解
if (f(a) > 0) :while err > rate : fa = math.fabs(f(a))fb = math.fabs(f(b))x = (fa * b + fb * a) / (fa + fb)if (f(x) == 0) :breakif (f(x) > 0) :err = math.fabs(x - a) / aa = xelse :err = math.fabs(x - b) / bb = xelse :while err > rate :fa = math.fabs(f(a))fb = math.fabs(f(b))x = (fa * b + fb * a) / (fa + fb)if (f(x) == 0) :breakif (f(x) > 0) :err = math.fabs(x - b) / bb = xelse :err = math.fabs(x - a) / aa = x #输出结果       
print("f(%.3lf) = %.3lf\n" %(x, f(x)))

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！