C#，数值计算，用割线法（Secant Method）求方程根的算法与源代码

割线法用于求方程 f(x) = 0 的根。它是从根的两个不同估计 x1 和 x2 开始的。这是一个迭代过程，包括对根的线性插值。如果两个中间值之间的差值小于收敛因子，则迭代停止。

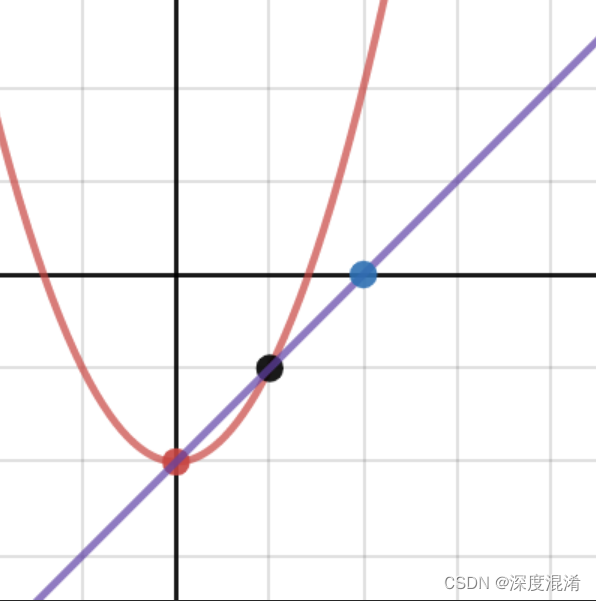
亦称弦截法，又称线性插值法.一种迭代法.指用割线近似曲线求方程根的2步迭代法.此法用通过点(xk，f(xk))及(xk-1，f(xk-1))的割线

近似曲线y=f(x)，用割线的根作为方程根的新近似xk+1，从而得到方程求根的割线法迭代程序

( k=1，2，…，n)，

其中x0，x1为初始近似.若f(x)在根x*的邻域内有二阶连续导数，且f′(x*)≠0，则当x0，x1在x*邻域内时，割线法收敛于x*，其收敛阶为

using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer.Algorithm
{
    public delegate double delegateFunctionX(double x);

    public static partial class Algorithm_Gallery
    {
        public static delegateFunctionX funx = null;

        public static bool Secant(double x1, double x2, out double x0, double Epsilon)
        {
            int n = 0;
            double xm;
            
            x0 = x1;
            if (funx(x1) * funx(x2) < 0)
            {
                do
                {
                    x0 = (x1 * funx(x2) - x2 * funx(x1))  / (funx(x2) - funx(x1));

                    double c = funx(x1) * funx(x0);

                    x1 = x2;
                    x2 = x0;

                    n++;

                    if (Math.Abs(c) < float.Epsilon)
                    {
                        break;
                    }
                    xm = (x1 * funx(x2) - x2 * funx(x1))  / (funx(x2) - funx(x1));

                } while (Math.Abs(xm - x0) >= Epsilon);
                return true;
            }
            else
            {
                return false;
            }
        }
    }
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！