动态规划求树的最大连通分支问题
目录
1.题目概述
2.算法分析
3.算法思路:
4.算法实现:
1.题目概述
问题描述:给定一棵树T,树中每个顶点u都有权值w(w),可以是负数。现在要找到树T的一个连通子图使该子图的权之和最大。
算法设计:对于给定的树T,计算树T的最大连通分支。
数据输入:第1行有1个正整数n,表示树T有n个顶点。树T的顶点编号为1,2,,n。第2行有n个整数,表示n个顶点的权值。接下来的n-1行中,每行有表示树T的一条边的2个整数u和v,表示顶点u与顶点v相连。
输入示例:
5
-1 1 3 1 -1
4 1
1 3
1 2
4 5
输出示例
4
2.算法分析
①问题特点
- 某棵树的权值之和,可以累加到树的根节点:从每一个叶节点沿着分支累加到根。
- 题目没有给出树的根,因此在连通的分支中,任何一个节点都可以作为根节点。
- 如果找到了题目要求的最大连通分支,那么可以将权值和累加到分支上的任何一个节点。
②解题策略
- 一个最大连通分支由许多的子分支构成:树A的权值和 = 根的权值 + 分支1权值和 + 分支2权值和 +……
- 题目要求最大的权值和,即我们要对分支有取舍:权值和>0的分支才可以贡献给根,我们希望这个分支是尽可能的大
- 大的问题:求树A的最大连通分支
- 分解子问题:组成树A的每一个小树的最大连通分支
- 说明:最终的解并非我们设定的树根上累加到的权值,因为图中每一个节点都不一定在最终需要的分支里面,而且每一个节点都有可能是要求的分支的根。所以答案是所有结点累加到的权值和里面最大的。
3.算法思路:
①分层:选择一个根节点x,对以x为根节点的树进行分层,设定每一个节点的父节点。
②遍历:对进行自底向上的遍历,对于某个节点 i ,如果 i 累加到的权值 wi > 0 ,则贡献给它的父节点 。
③最优解:遍历树,找到累加到的最大权值。
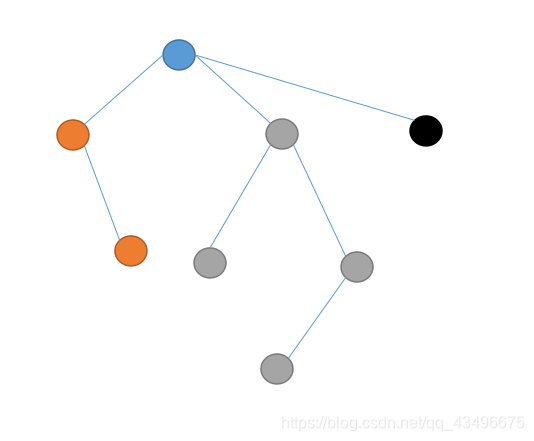
例如:
示例中的树,我们取节点1为根节点,把树分层:

从底至上解决子问题:
w[5]=-1 <0 贡献0给4
w[4]= 1+0 1 贡献1给1
w[3]= 3 贡献3给1
w[2]= 1 贡献1给1
w[1]= -1+1+3+1 = 4
最大的累加权值是节点1的权值和,题目答案是4
4.算法实现:
①分层的实现:使用广度优先遍历bfs,用栈记录遍历的顺序
②记录父节点,分层后所处的层次,累加后的权值:结构体node
③从底至上:利用分层后得到的栈,先进后出,pop出的结点是当前结点中最高层的
代码:
#include
#include
#include
#include
#include
using namespace std;
struct node{int w;int parent;int level;int visit;node(){w=parent=level=visit=0;}
};vector< list > adjList;//邻接链表
vector Node; //结点数组
stack rank;//分层后结果(栈顶到栈底,层次变低)void bfs(){queue q;list l;list::iterator iter;int cur,nxt;node son;//第一个节点先进去 q.push(1);rank.push(1);//从第一层开始广度优先遍历 while(!q.empty()){cur=q.front();//当前要访问的点 q.pop();l=adjList[cur];//得到当前点的邻接点链表 for(iter=l.begin();iter!=l.end();iter++){//将邻接点压入等待访问的队列 nxt=*iter;if(!Node[nxt].visit){q.push(nxt);//待访问 rank.push(nxt);son=Node[nxt];son.level=Node[cur].level+1;//确定层次 mson.parent=cur;//确定父结点 Node[nxt]=son;}}Node[cur].visit=1;//标记 }
} int main(){int n,i;cin>>n; adjList.assign(n+1,list());//n+1个链表 Node.assign(n+1,node());//n+1个点 //权值 for(i=1;i<=n;i++){cin>>Node[i].w;}//边int l,r;for(i=0;i>l>>r;adjList[l].push_back(r);adjList[r].push_back(l);} //确定层次和父结点 bfs();//动态规划自底向上根据每个节点的权值的正负,决定要不要贡献给父结点 int wei,cur,par;while(!rank.empty()){cur=rank.top();rank.pop();par=Node[cur].parent;Node[par].w+=max(0,Node[cur].w);} int max=Node[1].w,maxi=1;for(i=2;i<=n;i++){if(Node[i].w>max) {max=Node[i].w;maxi=i;}}cout<<"该树的最大连通分支的权值和是:"<
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!