【C++】对随机生成的有向图进行强连通分支分解
强连通分量. 有向图强 连通分量 :在 有向图 G中,如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点 强连通 (strongly connected)。. 如果有向图G的每两个顶点都强连通,称G是一个 强连通图 。. 有向图的极大强连通 子图 ,称为强连通分量。
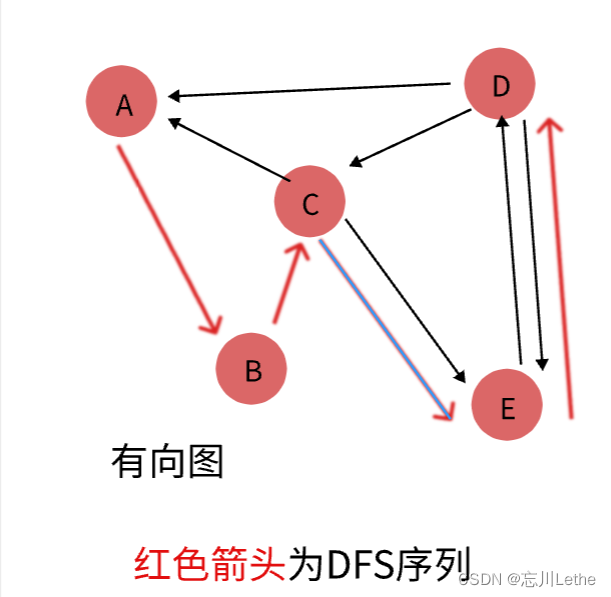
步骤1:在有向图上运行带时间戳的DFS;
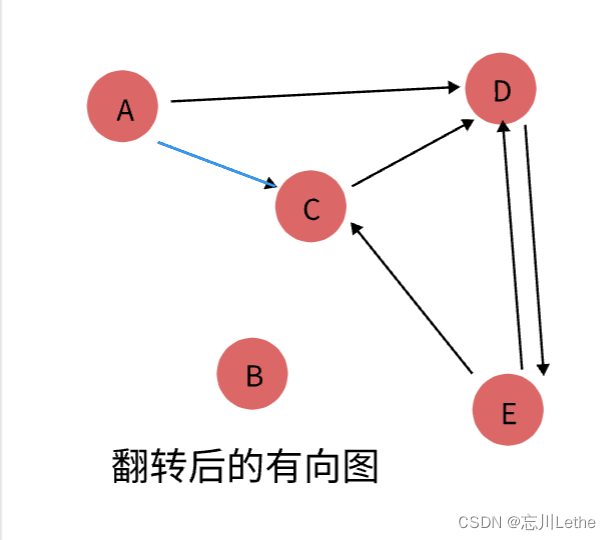
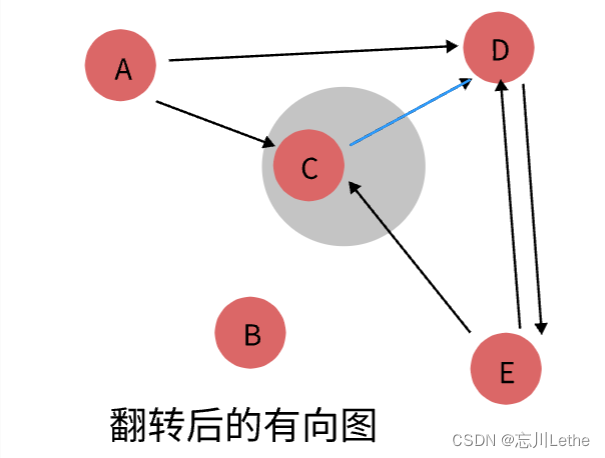
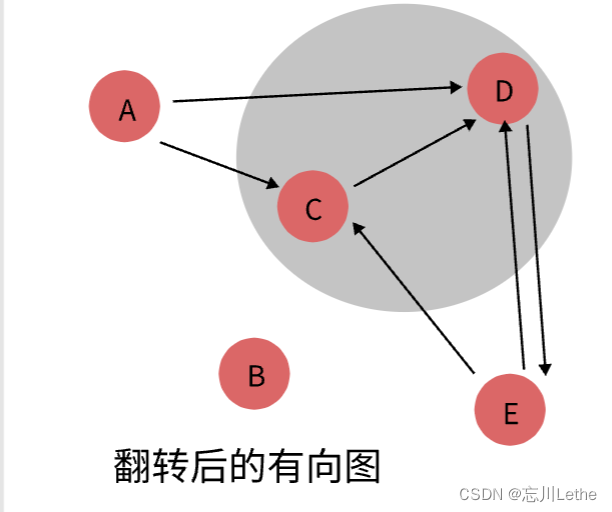
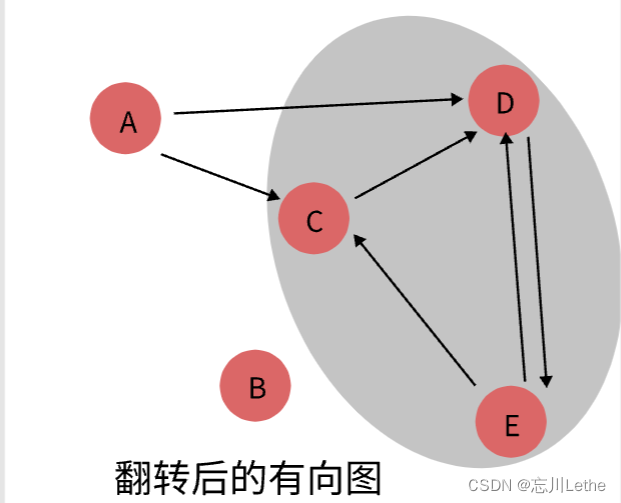
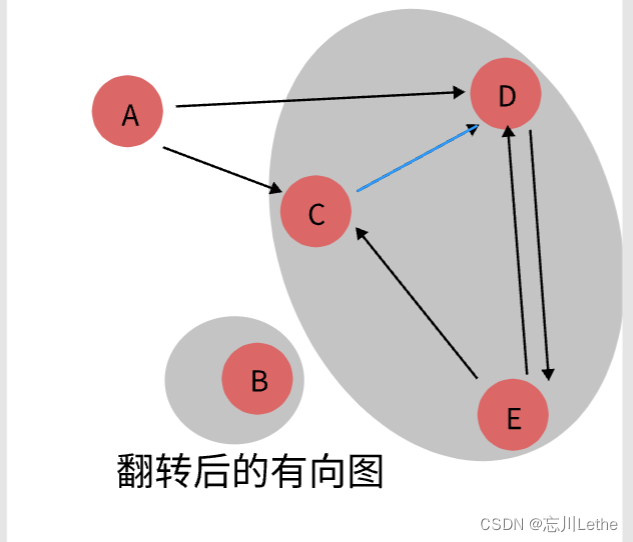
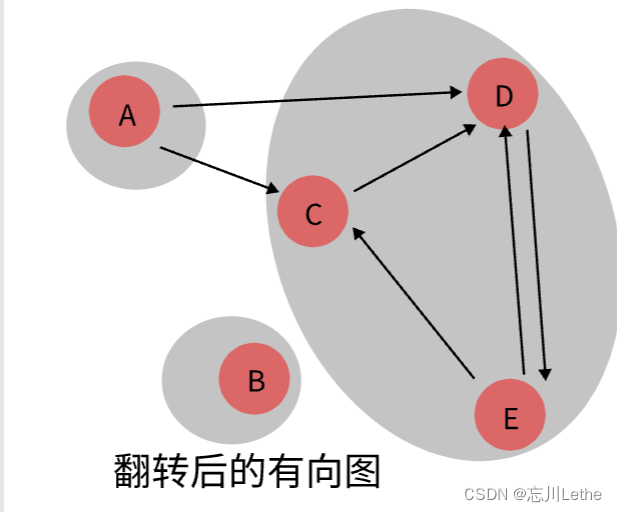
步骤2:在翻转的有向图上按照post值的大小运行DFS
vertexnum代表有向图的顶点数
a number greater than zero and less than one(for example: 0.3)表示的意思是任意两个顶点间存在有向边的概率
随后输入顶点的名字 比如就叫A B C D E 吧;
直接回车就能直接生成随机的有向图;
并获得分解后的各强连通分支。
#include
#include //概率
#include
#define MVNum 10
using namespace std;
int *pre;
int *post;
int *isvisited;
int myclock = 1; //时钟用于记录dist值
int g;
int p = 0; // super计数器
int h;//super_cout计数器
int V;//顶点数
int tempi;//from re_int 传递maxpost值
typedef struct ArcNode
{int adjvex;struct ArcNode *nextarc;
} ArcNode; //单链表表头-结构体typedef struct VNode
{char data;ArcNode *firstarc;
} VNode, AdjList[MVNum]; //图Graphtypedef struct
{AdjList vertices;int vertexnum;int arcnum;
} Graph;
typedef struct
{/* data */char shouldfristtobevisited;int newpost;int antiG_isvisited;
} supertable;supertable super[MVNum];void previsit(int u);
void postvisit(int u);
void TraverseAdjList(Graph &G)
{ // designed 遍历by Graph--lethefor (int i = 0; i < G.vertexnum; i++){cout << "【" << G.vertices[i].data << "】→"; //临时头指针用于遍历ArcNode *temp = G.vertices[i].firstarc; //当 temp 不为空,输出链表while (temp){ //输出顶点序号cout << "[" << temp->adjvex << "]";temp = temp->nextarc;if (temp)cout << "→";}putchar(10);}
}
void creatGraph(Graph &G, Graph &antiG)
{ //生成有向图及其反向图!!!double maybe=0; //两点之间存在边的概率cout << "please enter the number of vertex:";cin >> G.vertexnum;antiG.vertexnum = G.vertexnum;V=G.vertexnum;//antiGV=new char[G.vertexnum];isvisited = new int[G.vertexnum]; //访问标志数组for (int c = 0; c <= G.vertexnum; c++){isvisited[c] = 0;}pre = new int[G.vertexnum];post = new int[G.vertexnum];for (int e = 0; e <= G.vertexnum; e++){pre[e] = 0;}for (int f = 0; f <= G.vertexnum; f++){post[f] = 0;}cout << "please enter a number greater than zero and less than one(for example: 0.3):";cin >> maybe;maybe *= 10; //将概率转化为整数cout << "please enter the informnation of vertex:" << endl;srand((unsigned)time(NULL));for (int i = 0; i < G.vertexnum; i++){cin >> G.vertices[i].data;antiG.vertices[i].data = G.vertices[i].data;G.vertices[i].firstarc = NULL; //各顶点结点的指针域置空antiG.vertices[i].firstarc = NULL;super[i].shouldfristtobevisited=G.vertices[i].data;// p++;}for (int i = 0; i < G.vertexnum; i++){for (int j = 0; j < G.vertexnum; j++){if (i != j){if (rand() % 10 < int(maybe)){ArcNode *p1 = new ArcNode; //生成第一个边连接的结点(后面的那一个)p1->adjvex = j; //存入结点的下标 //关联头结点,用头插法,插入结点p1->nextarc = G.vertices[i].firstarc;G.vertices[i].firstarc = p1;ArcNode *p2 = new ArcNode;p2->adjvex = i; //存入结点的下标 //关联头结点,用头插法,插入结点p2->nextarc = antiG.vertices[j].firstarc;antiG.vertices[j].firstarc = p2;}}}}
}void explorer(Graph G, int u)
{isvisited[u] = 1; // 1 is true ,0 is falsecout << G.vertices[u].data << " ";//antiGV[p]=G.vertices[u].data;previsit(u);ArcNode *tempv = G.vertices[u].firstarc;int w;while (tempv){w = tempv->adjvex;if (!(isvisited[w])){explorer(G, w);}tempv = tempv->nextarc;}postvisit(u);
}void previsit(int u)
{pre[u] = myclock;myclock++;
}
void postvisit(int u)
{post[u] = myclock;myclock++;
}
void deepin(Graph G)
{for (g = 0; g < G.vertexnum; g++){if (!(isvisited[g])){explorer(G, g);}}
}int re_int(Graph GG){int max=-1;//char maxpostVindex;for( int i=0;imax)){max=super[i].newpost;tempi=i;}}return tempi;
}void explorerforbreakgraph(Graph &G, int u)
{super[u].antiG_isvisited = 1; // 1 is true ,0 is falsecout << G.vertices[u].data << " ";V--;ArcNode *tempv = G.vertices[u].firstarc;int w;while (tempv){w = tempv->adjvex;if (!super[w].antiG_isvisited){explorerforbreakgraph(G, w);}tempv = tempv->nextarc;}cout< 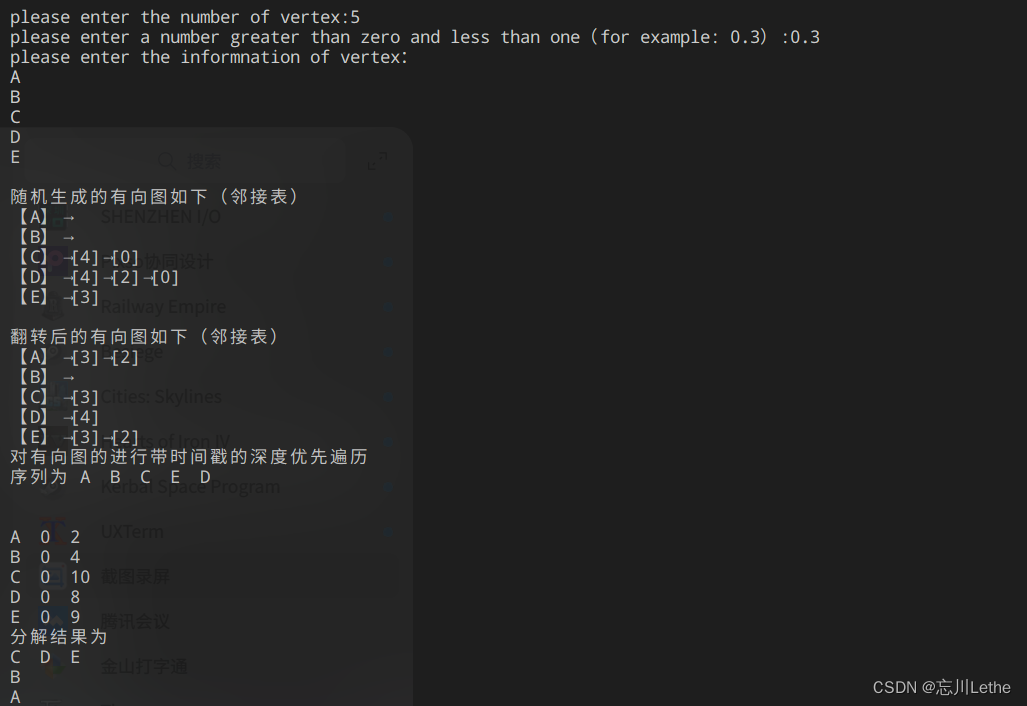
| 反向图顶点 | 访问标志 | postvisit |
| A | 0 | 2 |
| B | 0 | 4 |
| C | 0 | 10 |
| D | 0 | 8 |
| E | 0 | 9 |
注意:!!!【顶点数不能为6】
【顶点数不能为6】
【顶点数不能为6】否则会出错 原因还没找到
将就用用吧……
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!