概率论与数理统计——Chapter1随机事件

随机事件

• 事件与集合
• 事件间的关系
• • 包含关系
  • 相等关系
  • 互不相容（互斥）
  • 对立事件（互逆事件）
• 事件的运算
• • 交（积）∩
  • 并（和）∪
  • 差 —
• 事件运算的性质

事件与集合

样本点——集合元素
样本空间Ω——全集
事件——Ω的一个子集
一次试验，事件A发生了——试验结果ω∈A
通过这些，就可以建立事件与集合间更多的对应关系。集合论中的包含、相等等集合关系，交、并等集合运算对事件而言赋予了某些特定含义。

将事件相关知识在概率论语言与集合语言建立对应关系。

事件间的关系

包含关系

如果事件A的样本点都是事件B的样本点，
集合语言：则称A包含于B，或称B包含A，记为A⊂B，B⊃A，也称A是B的子集；
概率论语言：事件A发生必然导致事件B发生

相等关系

如果A,B事件满足：属于A的样本点都属于B，属于B的样本点都属于A，则称A,B相等
集合语言：A⊂B，B⊂A↔A=B，A,B是同一集合
概率论语言：事件A，B是同一事件

互不相容（互斥）

如果事件A与B没有相同的样本点，则称A与B互不相容。
集合语言：A∩B=∅
概率论语言：事件A与B不可能同时发生

对立事件（互逆事件）

A ‾ \overline{A} A，由在Ω中而不在A中的样本点组成的集合
集合语言： A ‾ = { x ∣ x ∉ A ∧ x ∈ Ω } ； A ∩ A ‾ = ∅ , 且 A ∪ A ‾ = Ω \overline{A}=\{x|x∉A∧x∈Ω\}；A∩\overline{A}=∅,且A∪\overline{A}=Ω A={x∣x∈/​A∧x∈Ω}；A∩A=∅,且A∪A=Ω
概率论语言：$A$不发生

注意
①对立事件是相互的
②对立事件一定是互不相容的事件，即 A ∩ A ‾ = ∅ A∩\overline{A}=∅ A∩A=∅，但互不相容的事件不一定是对立事件
③$A，B$互为对立事件$\leftrightarrow A\cap B=\varnothing 且A\cup B=\Omega$

事件的运算

交（积）∩

由事件A与B中公共的样本点组成，
集合语言：用A∩B，（或AB）表示，A∩B⊂A，A∩B⊂B
概率论语言：事件A与B同时发生
推广：事件 A 1 A_1 A1​，…， A n A_n An​同时发生，称为 A 1 A_1 A1​，…， A n A_n An​的积事件，

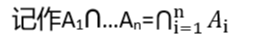
并（和）∪

由事件A与B中所有的样本点组成
集合语言：A∪B，A⊂A∪B，B⊂A∪B
概率论语言：事件A与B中至少有一个发生
推广，事件 A 1 A_1 A1​，…， A n A_n An​中至少一个发生，称为 A 1 A_1 A1​，…， A n A_n An​的和事件，

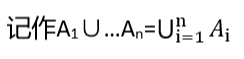
差 —

由在事件A中但不在事件B中的样本点组成的集合
集合语言： A − B ， A − B = A ∩ B ‾ A-B，A-B=A∩\overline{B} A−B，A−B=A∩B
概率论语言：事件A发生而B不发生
A ‾ = Ω − A \overline{A}=Ω-A A=Ω−A

事件运算的性质

交换律
A∩B=B∩A，A∪B=B∪A

结合律
(A∩B）∩C=A∩（B∩C）
(A∪B）∪=A∪（B∪C）

分配律
（A∪B）∩C=（A∩C）∪（B∩C）
（A∩B）∪C=（A∪C）∩（B∪C）

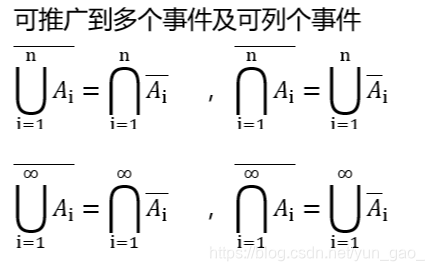
对偶律（德摩根公式)

事件A,B并的对立等于A对立与B对立的交：
集合语言： ( A ∪ B ) ‾ \overline{(A∪B)} (A∪B)​= A ‾ \overline{A} A∩ B ‾ \overline{B} B
概率论语言：A,B都不发生=A不发生且B不发生

事件交的对立等于对立的并：
集合语言： ( A ∩ B ) ‾ \overline{(A∩B)} (A∩B)​= A ‾ \overline{A} A∪ B ‾ \overline{B} B
概率论语言：A,B不都发生=A不发生或者B不发生

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！