使用matlab绘制弧线,[计算机图形学经典算法] 直线段和圆弧在屏幕上的绘制 （附matlab代码）...

刚学习了计算机图形学这门课程，为奠定根基的算法所倾倒，特此记录一二。

直线—中点 Bresenham 算法

DDA算法在效率上较低的原因是需要计算 k，并以之作为累加项。一个直观的改进方式，是在整个运算过程中将涉及到的数值乘以 dx (或dy)，转化为整型进行运算。

中点 Bresenham 算法采用一种不同的观点来解决这一问题－判别式。我们先考虑一般的直线方程，在图形学中我们一般给出的已知条件是两个端点：

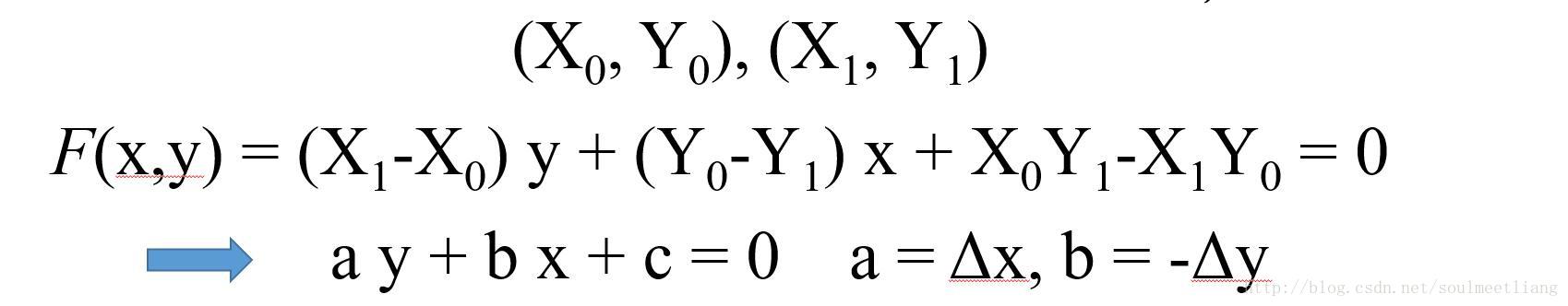
此判别方程的意义，在于直线上的所有点均使 F(x,y)=0。

现在，我们考虑离散的情形，在|k| < 1时，为判断如下图所示的与P相邻的像素点Pd和Pu中的哪一个归属于直线，我们取两者的中点M作为判决依据。将其坐标代入判别式

(1) F(M) < 0, 取上方点 Pu

(2) F(M) > 0, 取下方点 Pd

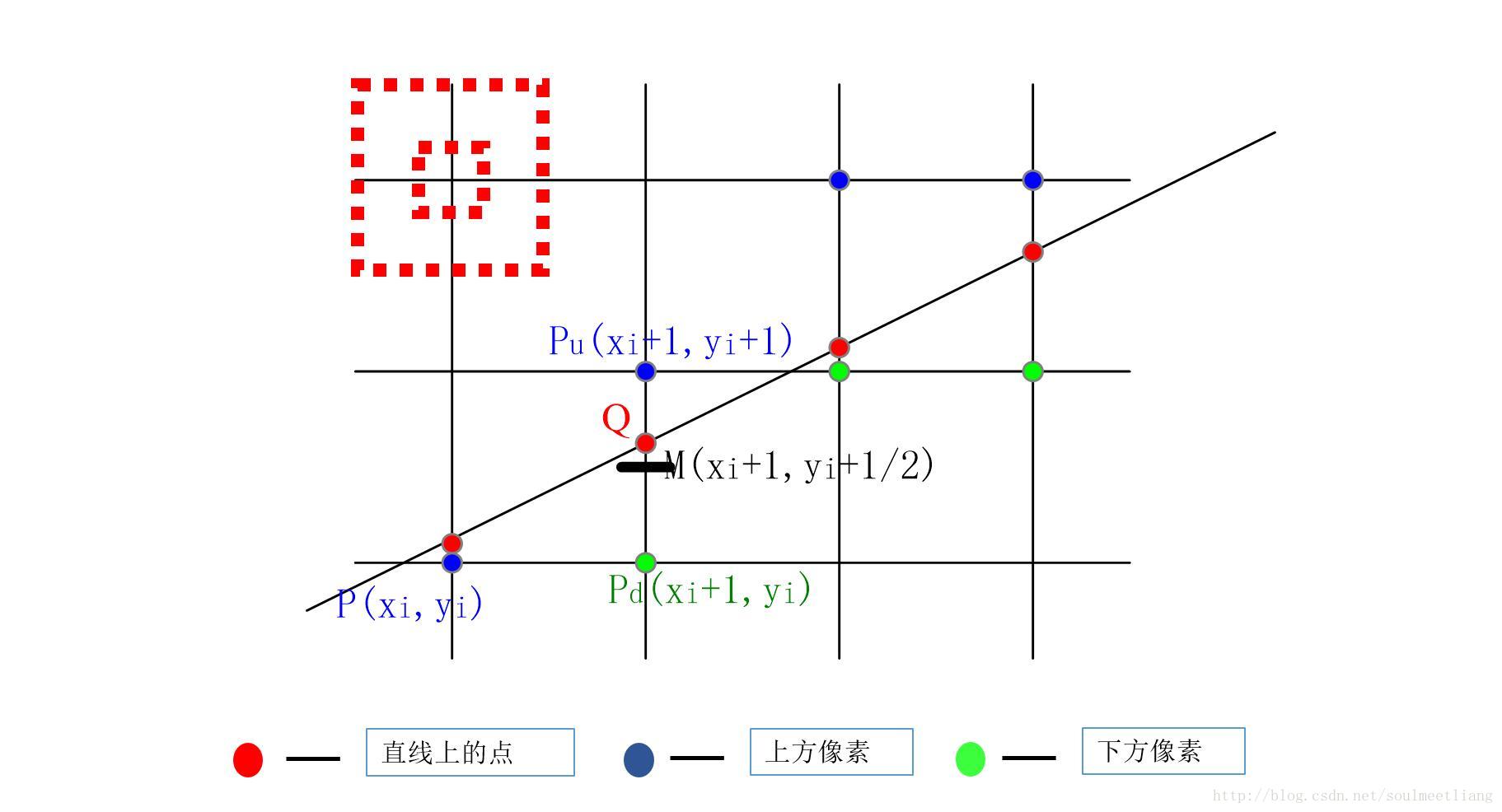
因此，若(Xi, Yi)为直线上的点，在判定下一个点(Xi＋1,Yi+1)并在(Xi＋1,Yi+1)和(Xi＋1,Yi)中进行选择时，可以根据中点坐标(Xi＋1,Yi+0.5)代入判别式进行判定。

F(Xi,Yi) = a Yi + b Xi + c = 0

F(Xi＋1,Yi+0.5) = a Yi + 0.5a + b Xi + b +c

= 0.5a + b

(1) F(M) = 0.5a + b < 0, 取上方点 Pu (Xi＋1,Yi+1)

(2) F(M) = 0.5a + b > 0, 取下方点 Pd (Xi＋1,Yi)

两个问题：

(1) F(Xi,Yi)=0 不一定总能满足，如何解决？

(2) 尽管 a, b, c 均为整数(?)，仍有一个0.5为小数。

问题(2)容易解决，仅需在计算过程中乘2即可；

问题(1)则较为麻烦。我们知道在起始点时，F(Xi,Yi)=0 总是成立的，在后续计算中我

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！