Fourier Series 傅立叶级数 学习笔记Part 2

Part 2 按我的理解，会包括下面的三个部分，区间变换和奇偶函数变换。

区间变换

在part 1 里，我们的区间范围是$[-\pi ,\pi ]$,世界上哪来那么多正正好好的周期是$2\pi$的周期函数。那么就要变换。
这里的变换也很简单 $y=\pi x/l$，然后函数就变成了关于y的周期是$2\pi$的周期函数。

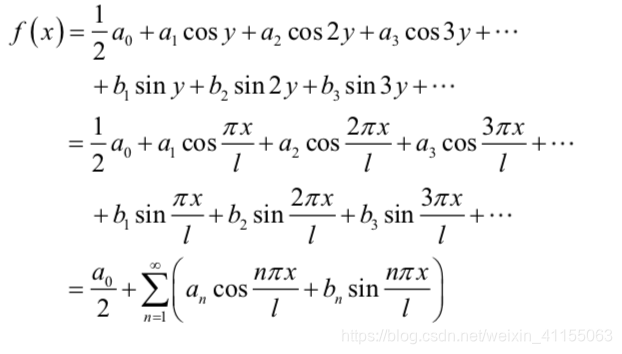
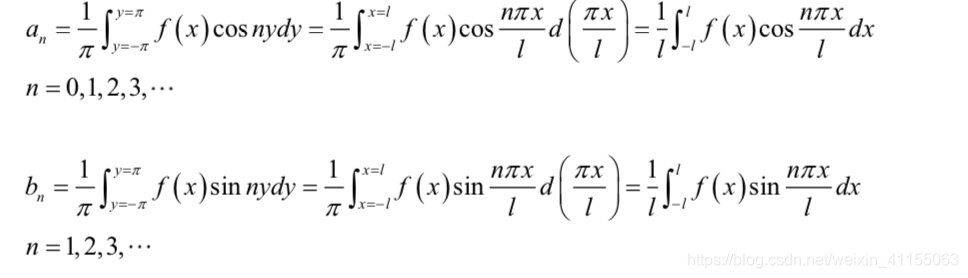
整理之后的样子，我想，大多数的学渣，如我，都是会的东西局限到这里或者是下面的部分

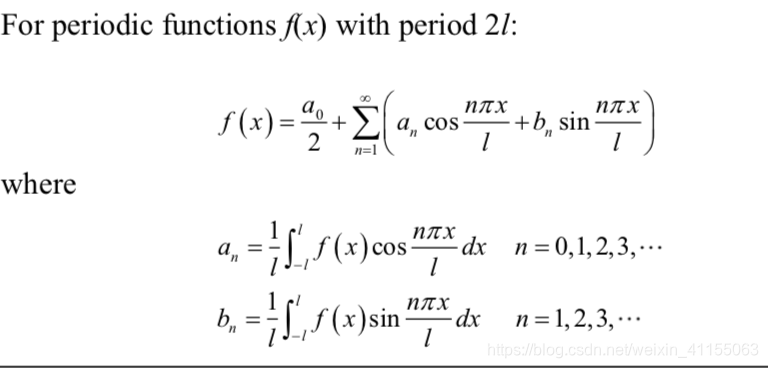
奇偶函数

接上式

偶函数

偶函数就是 b n = 0 b_{n}=0 bn​=0

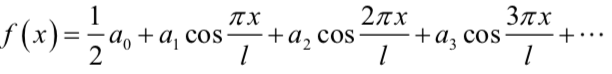
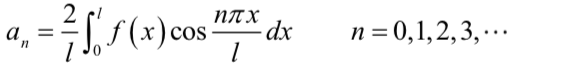
奇函数

奇函数就是 a n = 0 a_{n}=0 an​=0

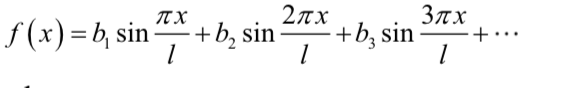
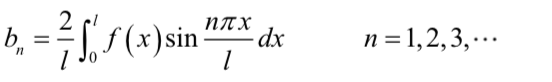
我们可以看到在奇偶函数的系数中积分上下限发生了变化，这是利用函数的对称性在做积分时做的变换。

奇偶函数的延伸

这一部分给我的感觉就是之前的所有的内容的综合应用。
我先把结果放上来

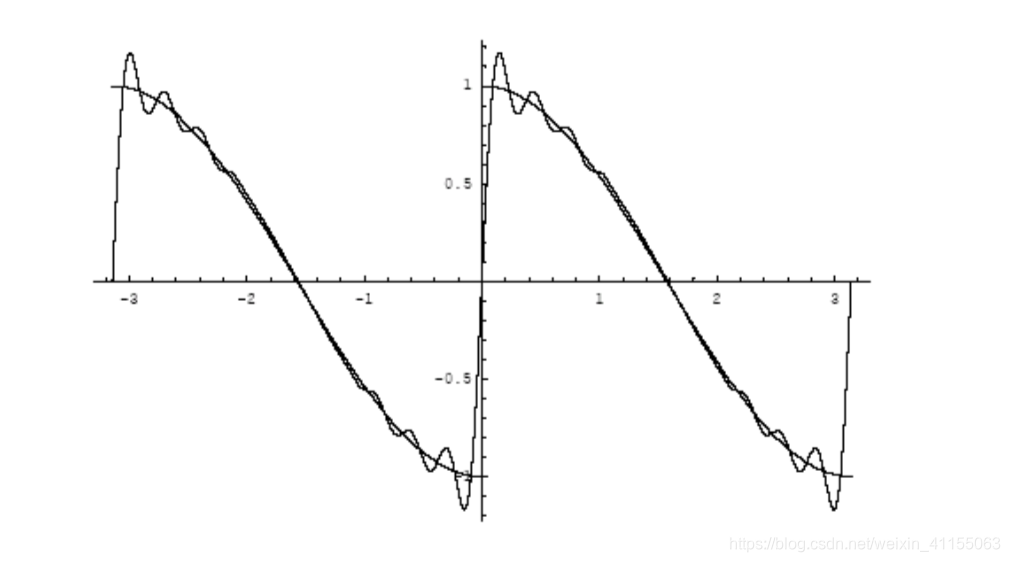
函数是

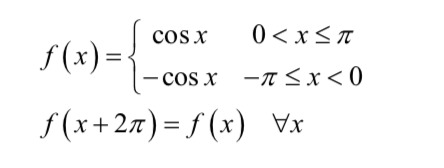
思路是，首先这个函数是一个奇函数，应该按照奇函数的方式处理系数。

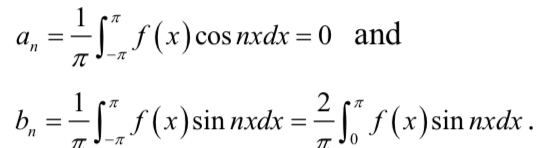
对 b n b_{n} bn​化简，然后对n的奇偶性进行分段

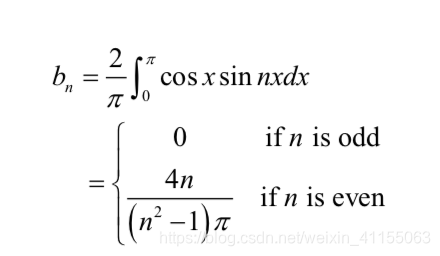
化简之后可以得到

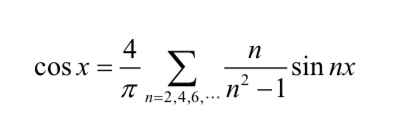
下一步就是对$[-\pi ,0]$的情况的进行处理

然后画图就可以通过n的增大，不断趋近于原函数。

此处有用到狄利克雷定理。

这是Numerical Methods and Modeling in Science 讲傅立叶XX的第一讲，看是可以看懂的。
后面逐渐进入到我理解不了的状态。。。
More Practice！

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！