算法练习day10——190328(根据指定值划分单链表、复制含有rand指针节点的链表、两个单链表相交)
1.将单向链表按某值划分成左边小、 中间相等、 右边大的形式
【题目】 给定一个单向链表的头节点head, 节点的值类型是整型, 再给定一个整数pivot。 实现一个调整链表的函数, 将链表调整为左部分都是值小于 pivot的节点, 中间部分都是值等于pivot的节点, 右部分都是值大于 pivot的节点。除这个要求外, 对调整后的节点顺序没有更多的要求。 例如: 链表9->0->4->5->1, pivot=3。 调整后链表可以是1->0->4->9->5, 也可以是0->1->9->5->4。 总之, 满 足左部分都是小于3的节点, 中间部分都是等于3的节点(本例中这个部分为空) , 右部分都是大于3的节点即可。 对某部分内部的节点顺序不做 要求。
进阶: 在原问题的要求之上再增加如下两个要求。在左、 中、 右三个部分的内部也做顺序要求, 要求每部分里的节点从左 到右的顺序与原链表中节点的先后次序一致。 例如: 链表9->0->4->5->1, pivot=3。调整后的链表是0->1->9->4->5。 在满足原问题要求的同时, 左部分节点从左到右为0、 1。 在原链表中也 是先出现0, 后出现1; 中间部分在本例中为空, 不再讨论; 右部分节点 从左到右为9、 4、 5。 在原链表中也是先出现9, 然后出现4,最后出现5。如果链表长度为N, 时间复杂度请达到O(N), 额外空间复杂度请达到O(1)。
1.1 分析
方法一:可用数组,转换为荷兰国旗问题,但是需要额外空间,并且不具有稳定性。
方法二:三个辅助节点:less、equal、more
- 先遍历一遍:
- 找到第一个小于privot的节点,赋值给less;
- 找到第一个等于privot的节点,赋值给equal;
- 找到第一个大于privot的节点,赋值给more;
- 第二次遍历时:
- 发现小于privot的,看是不是less,不是,就续在less后面;
- 发现等于privot的,看是不是equal,不是,就续在equal后面;
- 发现大于privot的,看是不是more,不是,就续在more后面;
- 最后,把equal连在less链表的后面,more连在equal链表的后面。
- 注意便捷问题:某个部分为空。
1.2 代码实现
此处为方法二的代码实现:
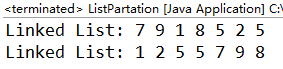
package Solution;public class ListPartation {public static void main(String[] args) {Node head1 = new Node(7);head1.next = new Node(9);head1.next.next = new Node(1);head1.next.next.next = new Node(8);head1.next.next.next.next = new Node(5);head1.next.next.next.next.next = new Node(2);head1.next.next.next.next.next.next = new Node(5);printLinkedList(head1);head1 = listPartation(head1, 5);printLinkedList(head1);}public static Node listPartation(Node head,int num) {Node help=head;Node next=null;Node less=null;Node equal=null;Node more=null;Node endl=null;Node ende=null;Node endm=null;while(help!=null) {//要断开,否则连接时后面不好判断next = help.next;help.next = null;if(help.value运行结果:
连接时代码的简化版:
// small and equal reconnect
if (endl != null) {endl.next = equal;ende = ende == null ? endl : ende;
}
// all reconnect
if (ende != null) {ende.next = more;
}
return less != null ? less : equal != null ? equal : more;注意:分区时,记得断开原链表的next,否则后面再连接时判断是否为null时就会混乱。——代码实现中辅助节点next作用就是这个。
2. 复制含有随机指针节点的链表
【题目】 一种特殊的链表节点类描述如下:
public class Node {public int value; public Node next;public Node rand;public Node(int data) {this.value = data;}
} - Node类中的value是节点值;
- next指针和正常单链表中next指针的意义一 样, 都指向下一个节点;
- rand指针是Node类中新增的指针, 这个指针可能指向链表中的任意一个节点, 也可能指向null。
给定一个由Node节点类型组成的无环单链表的头节点head, 请实现一个函数完成这个链表中所有结构的复制, 并返回复制的新链表的头节点。
进阶:不使用额外的数据结构, 只用有限几个变量, 且在时间复杂度为 O(N)内完成原问题要实现的函数。
2.1 分析
考虑使用哈希表(
哈希表的增删改查均为常数时间。
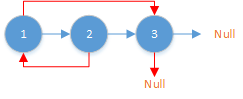
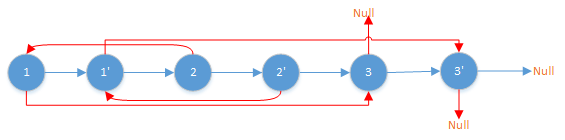
蓝色为next,红色为rand。
首先建立哈希表,存放<当前节点,它的拷贝节点>:
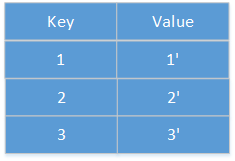
然后建立关系:
- 取出1和1'。
- 然后根据原链表得到1的next——2和rand——3。
- 查哈希表,得到2和3的对应拷贝节点2'和3'。
- 根据原节点建立拷贝节点的next和rand。

2.2 代码实现
package Solution;import java.util.HashMap;class RNode{int value;RNode next;RNode rand;public RNode(int value) {this.value=value;}
}
public class RandListCopy {public static void main(String[] args) {RNode head = null;RNode res1 = null;RNode res2 = null;printRandLinkedList(head);res1 = randListCopy(head);printRandLinkedList(res1);res2 = randListCopy(head);printRandLinkedList(res2);printRandLinkedList(head);System.out.println("=========================");head = new RNode(1);head.next = new RNode(2);head.next.next = new RNode(3);head.next.next.next = new RNode(4);head.next.next.next.next = new RNode(5);head.next.next.next.next.next = new RNode(6);head.rand = head.next.next.next.next.next; // 1 -> 6head.next.rand = head.next.next.next.next.next; // 2 -> 6head.next.next.rand = head.next.next.next.next; // 3 -> 5head.next.next.next.rand = head.next.next; // 4 -> 3head.next.next.next.next.rand = null; // 5 -> nullhead.next.next.next.next.next.rand = head.next.next.next; // 6 -> 4printRandLinkedList(head);res1 = randListCopy(head);printRandLinkedList(res1);res2 = randListCopy(head);printRandLinkedList(res2);printRandLinkedList(head);System.out.println("=========================");}public static RNode randListCopy(RNode head) {HashMap map=new HashMap();RNode cur=head; while(cur!=null) {map.put(cur, new RNode(cur.value));cur=cur.next;}cur=head;while(cur!=null) {map.get(cur).next=map.get(cur.next);map.get(cur).rand=map.get(cur.rand);cur=cur.next;}return map.get(head);}public static void printRandLinkedList(RNode head) {RNode cur = head;System.out.print("order: ");while (cur != null) {System.out.print(cur.value + " ");cur = cur.next;}System.out.println();cur = head;System.out.print("rand: ");while (cur != null) {System.out.print(cur.rand == null ? "- " : cur.rand.value + " ");cur = cur.next;}System.out.println();}
}
运行结果:

上述方法需要O(N)的额外存储空间(哈希表)。
2.3 分析(不用额外辅助空间的)
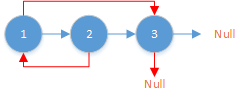
![]()
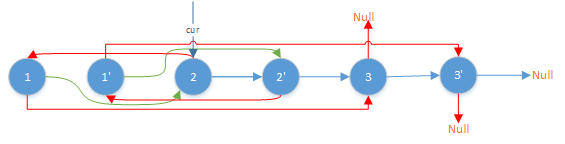
将拷贝节点放在原节点的next上。以这种方式省略哈希表的使用。
然后依次取出两个节点1和1'。
1的rand指向3,则取出3的拷贝节点3'。令1'的rand指向3'。

如此建立2'和3'的rand:
最后分离原链表的节点。
设置cur(当前原节点)、next(下一个原节点)、copy(当前原节点的拷贝节点)以及拷贝链表的表头result。
- cur=head;
- result=head.next;
- next=cur.next.next;
- copy=cur.next;
- 确定当前节点拷贝节点的后继:copy.next=next==null?null:next;
- 当前节点的后继指向下一个原节点:cur.next=netx;
- 当前节点后移cur=next;
2.4 代码实现
package Solution;public class RandListCopy {public static RNode randListCopy(RNode head) {if (head == null) {return null;}RNode cur=head;RNode next=null;RNode copy=null;while(cur!=null) {next=cur.next;copy=new RNode(cur.value);cur.next=copy;copy.next=next;cur=next;}cur=head;while(cur!=null) {copy=cur.next;copy.rand=cur.rand==null?null:cur.rand.next;cur=copy.next;}RNode result=head.next;cur=head;while(cur!=null) {//要分离两个链表next=cur.next.next;//下一个原节点copy=cur.next;copy.next=next==null?null:next.next;cur.next=next;cur=next;}return result;}
}
3.两个单链表相交的一系列问题
【题目】 在本题中, 单链表可能有环, 也可能无环。 给定两个单链表的头节点 head1和head2, 这两个链表可能相交, 也可能不相交。 请实现一个函数, 如果两个链表相交, 请返回相交的第一个节点; 如果不相交, 返回null 即可。
要求: 如果链表1的长度为N, 链表2的长度为M, 时间复杂度请达到 O(N+M), 额外空间复杂度请达到O(1)。
3.1 判断一个单链表是否有环
有环:返回第一个入环节点;
无环:返回空。
3.1.1 方法一:使用哈希表
用HashSet,只需要存key。
遍历链表,把当前遍历到的节点存入表。存之前需查看表中是否已有这个节点。
- 有,链表存在环,且这个已存在的节点是环的第一个入口节点;
- 没有,继续遍历;
- 最终next为空,则说明没有环。
3.1.2 方法二:使用两个指针
快指针F和慢指针S:
- F每次走两步;
- S每次走一步。
两个相遇时,肯定有环,此时F回到head处,一次走一步,当F与S再次相遇时,肯定是入环的头一个节点。
若F首先碰到空,则无环。
对head1和head2都调用判断是否有环的这个方法,
- 若都返回null:判断两个无环链表是否相交。
- 若一个有环,一个无环:不可能相交。
- 两个都有环:判断两个有环的链表是否相交。
3.2 判断两个无环链表是否相交
3.2.1 方法一:用Map
将链表1的所有节点放到map中;
遍历链表2,对于链表2的每一个节点,都查这个节点是否在map中:
- 第一个在的,就是第一个相交的节点;
- 若链表2已经遍历到空,还没有已存在于map中的节点,说明不相交。
3.2.2 方法二:
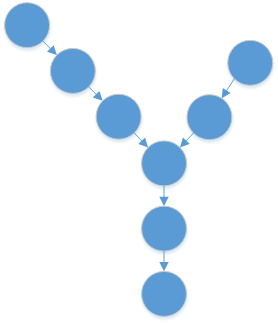
遍历链表1,得到其长度len1,以及拿到最后一个节点end1;
遍历链表2,得到其长度len2,以及拿到最后一个节点end2;
判断end1和end2是否相等,本题比较的都是内存地址(是否为同一个节点)。
- end1≠end2,不可能相交。
- end1=end2,说明相交,但这个点未必是第一个相交的节点。需要继续处理:
- 若len1=100,len2=80,则head1先走20步;
- 然后head1和head2一起走,他们一定可以一块走到相交的节点处。
3.3 判断两个有环的链表是否相交
有三种拓扑结构:
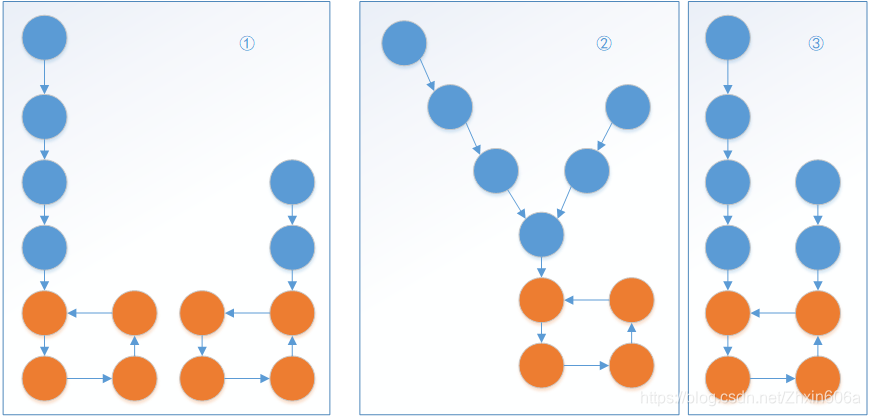
若loop1==loop2(入环节点一样),则是第二种情况;
- 截断环,如下图:
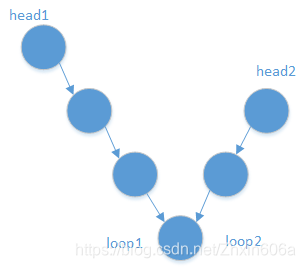
- 变为了3.2
若loop1!=loop2,可能是结构①,也可能是结构③。
区分方法:
- 让loop1一直往下走(取next);
- 若loop1都走一圈走到自己了,还没遇到loop2,则是结构1;
- 若遇到loop2,则是结构3。
- 返回loop1或loop2都行
- loop1是距head1最近的相交的节点;
- loop2是距head2最近的相交的节点。
3.4 代码实现
package Solution;import Solution.Test.Node;public class GetIntersectNode {public static void main(String[] args) {// 1->2->3->4->5->6->7->nullNode head1 = new Node(1);head1.next = new Node(2);head1.next.next = new Node(3);head1.next.next.next = new Node(4);head1.next.next.next.next = new Node(5);head1.next.next.next.next.next = new Node(6);head1.next.next.next.next.next.next = new Node(7);// 0->9->8->6->7->nullNode head2 = new Node(0);head2.next = new Node(9);head2.next.next = new Node(8);head2.next.next.next = head1.next.next.next.next.next; // 8->6System.out.println(getIntersectNode(head1, head2).value);//输出6// 1->2->3->4->5->6->7->4...head1 = new Node(1);head1.next = new Node(2);head1.next.next = new Node(3);head1.next.next.next = new Node(4);head1.next.next.next.next = new Node(5);head1.next.next.next.next.next = new Node(6);head1.next.next.next.next.next.next = new Node(7);head1.next.next.next.next.next.next = head1.next.next.next; // 7->4// 0->9->8->2...head2 = new Node(0);head2.next = new Node(9);head2.next.next = new Node(8);head2.next.next.next = head1.next; // 8->2System.out.println(getIntersectNode(head1, head2).value);//输出2// 0->9->8->6->7->4->5->6..head2 = new Node(0);head2.next = new Node(9);head2.next.next = new Node(8);head2.next.next.next = head1.next.next.next.next.next; // 8->6System.out.println(getIntersectNode(head1, head2).value);//输出6或4}public static Node getIntersectNode(Node head1,Node head2) {if(head1==null||head2==null)return null;Node loop1=getLoopNode(head1);Node loop2=getLoopNode(head2);if(loop1==null&&loop2==null)//都无环,3.1return noLoop(head1,head2);if(loop1!=null&&loop2!=null)//都有环,三种结构return bothLoop(head1,loop1,head2,loop2);return null;}public static Node getLoopNode(Node head) {if(head==null||head.next==null||head.next.next==null)return null;Node quick=head.next.next;Node slow=head.next;while(quick!=slow) {if(quick.next==null||quick.next.next==null)//无环return null;quick=quick.next.next;slow=slow.next;}//快指针和慢指针相遇,有环quick=head;while(quick!=slow) { quick=quick.next;slow=slow.next;} return quick;}public static Node noLoop(Node head1,Node head2) {int len=0;Node cur1=head1;Node cur2=head2;while(cur1.next!=null) {len++;cur1=cur1.next;}while(cur2.next!=null) {len--;cur2=cur2.next;}if(cur1!=cur2)//末尾节点不在一块,肯定不相交return null;//cur1为长链表cur1=len>0?head1:head2;cur2=cur1==head1?head2:head1;len=Math.abs(len);while(len>0) {cur1=cur1.next;len--;}while(cur1!=cur2) {cur1=cur1.next;cur2=cur2.next;}return cur1;}public static Node bothLoop(Node head1,Node loop1,Node head2,Node loop2) {Node cur1=head1;Node cur2=head2;if(loop1==loop2) {//结构2int len=0;while(cur1!=loop1) {len++;cur1=cur1.next;}while(cur2!=loop2) {len--;cur2=cur2.next;}//cur1为长链表cur1=len>0?head1:head2;cur2=cur1==head1?head2:head1;len=Math.abs(len);while(len>0) {cur1=cur1.next;len--;}while(cur1!=cur2) {cur1=cur1.next;cur2=cur2.next;}return cur1;}else {//判断结构1还是结构3cur1=loop1.next;while(cur1!=loop2) {if(cur1==loop1)//没遇到loop2,先遇到自己,结构1,return null;cur1=cur1.next; }//遇到loop2,结构3return loop1;}}
}
运行结果:

三种示例结构为:
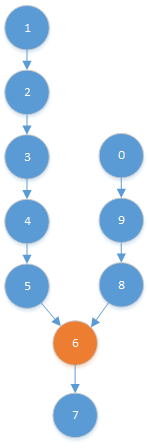
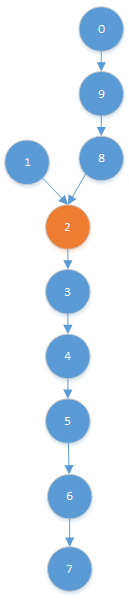
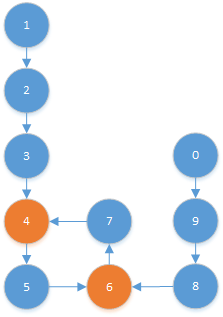
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!