1.实现二叉树的先序、 中序、 后序遍历， 包括递归方式和非递归方式

1.1 访问节点的顺序

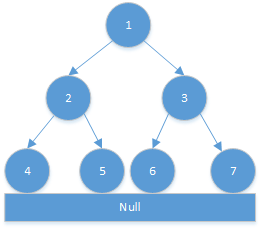
节点访问顺序如下图所示：

访问顺序：1 2 4 4 4 2 5 5 5 2 1 3 6 6 6 3 7 7 7 3 1

先序遍历：当节点第一次出现时就打印——1 2 4 5 3 6 7 （1 2 4 4 4 2 5 5 5 2 1 3 6 6 6 3 7 7 7 3 1）

中序遍历：当节点出现第二次时就打印——4 2 5 1 6 3 7 （1 2 4 4 4 2 5 5 5 2 1 3 6 6 6 3 7 7 7 3 1）

后序遍历：当节点出现第三次时才打印——4 5 2 6 7 3 1 （1 2 4 4 4 2 5 5 5 2 1 3 6 6 6 3 7 7 7 3 1）

1.2 递归实现

package Tree;public class VisitNode {public static void main(String[] args) {Node head = new Node(1);head.left = new Node(2);head.right = new Node(3);head.left.left = new Node(4);head.left.right = new Node(5);head.right.left = new Node(6);head.right.right = new Node(7);preOrder(head);System.out.println();inOrder(head);System.out.println();postOrder(head);System.out.println();}public static void preOrder(Node root) {if(root==null)return;System.out.print(root.value+" ");preOrder(root.left);preOrder(root.right);}public static void inOrder(Node root) {if(root==null)return;inOrder(root.left);System.out.print(root.value+" ");inOrder(root.right);}public static void postOrder(Node root) {if(root==null)return;postOrder(root.left);postOrder(root.right);System.out.print(root.value+" ");}
}

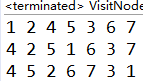
运行结果：

1.3 非递归实现

1.3.1 先序遍历

分析：

需要用到一个辅助栈。

• 先把根节点压入栈中；
• 栈不为空时，弹出一个元素，并打印；
• 若它右孩子不为空，右孩子入栈，若左孩子不为空，左孩子也入栈。

代码实现：

public static void preOrderUnRecur(Node root) {System.out.println("preOrderUnRecur:");if(root!=null) {Stack stack=new Stack();stack.push(root);while(!stack.isEmpty()) {Node cur=stack.pop();System.out.print(cur.value+" ");if(cur.right!=null)stack.push(cur.right);if(cur.left!=null)stack.push(cur.left);}}System.out.println();
}

1.3.2 中序遍历

分析：

当前节点不为空时，先把自己的压到栈中，然后向左孩子移动；

当前节点为空时，栈顶元素出栈，打印，然后向栈顶元素的右孩子移动。

步骤：

压入1，1的左孩子2，2的左孩子4。

4 的左孩子为空，栈顶元素出栈：

然后4向它的右孩子走，还为空，栈顶元素出栈：

然后2向它的右孩子5走，不为空，入栈：

5向左孩子走，为空，栈顶元素出栈：

5向右孩子走，还为空，栈顶元素出栈：

1向它的右孩子3走，不为空，入栈.....（后面不再赘述）

代码实现：

public static void inOrderUnRecur(Node root) {System.out.println("inOrderUnRecur:");if(root!=null) {Stack stack=new Stack();while(!stack.isEmpty()||root!=null) {if(root!=null) {//以节点不为空的条件进来stack.push(root);root=root.left;}else {//以栈不为空的条件进来root=stack.pop();System.out.print(root.value+" ");root=root.right;}}}System.out.println();
}

1.3.3 后序遍历

分析：

先序遍历的打印顺序是：中左右，现在调整为中右左，就是：

先压入当前节点的右孩子，再压左孩子。

然后打印顺序就为中右左。

后序遍历打印顺序是：左右中，和目前已实现的顺序刚好相反。使用栈来实现顺序反转。

代码实现：

public static void postOrderUnRecur(Node root) {System.out.println("postOrderUnRecur:");Stack help=new Stack();if(root!=null) {Stack stack=new Stack();stack.push(root);while(!stack.isEmpty()) {Node cur=stack.pop();help.push(cur);if(cur.left!=null)stack.push(cur.left);if(cur.right!=null)stack.push(cur.right);}}while(!help.isEmpty())System.out.print(help.pop().value+" ");System.out.println();
}

2.打印一个二叉树

3.在二叉树中找到一个节点的后继节点

【题目】 现在有一种新的二叉树节点类型如下：

public class Node {public int value;public Node left;public Node right; public Node parent;public Node(int data) {this.value = data;}
}

该结构比普通二叉树节点结构多了一个指向父节点的parent指针。

假设有一 棵Node类型的节点组成的二叉树， 树中每个节点的parent指针都正确地指向自己的父节点， 头节点的parent指向null。

只给一个在二叉树中的某个节点 node， 请实现返回node的后继节点的函数。

在二叉树的中序遍历的序列中， node的下一个节点叫作node的后继节点。

3.1 分析

方法1：

可以根据给定节点的parent指针回到根节点（parent为空的节点），然后进行一次中序遍历，得到中序序列，即可得到这个节点的后继节点。——复杂度是遍历整棵树

方法2：

——复杂度是当前节点到它后继的距离。

3.2 方法2的具体分析

当前节点若有右子树，则它的后继节点是右子树的最左节点；

若当前节点没有右子树：

• 找以当前节点作为左子树最后一个节点的节点：
• 
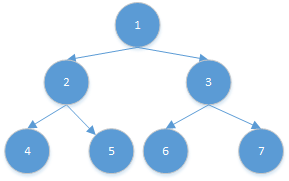
• 比如节点4，它是作为节点2的左子树的最后一个节点的，节点2即为要找的节点；
• 比如节点5，它是作为节点1的左子树的最后一个节点的，节点1即为要找的节点。

具体寻找方法：

• 当前节点通过parent指针找到父节点；
• 它是父节点的左孩子吗？
  • 不是，继续往上走；
  • 是，那后继节点就为这个父节点。

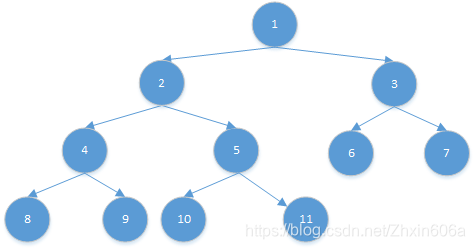
比如，给定的节点是11。

它的父节点是5，11不是5的左孩子，继续往上；

5的父节点是2，5不是2的左孩子，继续往上；

2的父节点是1，2是1的左孩子，则11的后继节点是1。

3.3 代码实现

package Tree;public class GetSuccessorNode {public static class Node{Node left;Node right;Node parent;int value;public Node(int value) {this.value=value;}}public static void main(String[] args) {Node head = new Node(6);head.parent = null;head.left = new Node(3);head.left.parent = head;head.left.left = new Node(1);head.left.left.parent = head.left;head.left.left.right = new Node(2);head.left.left.right.parent = head.left.left;head.left.right = new Node(4);head.left.right.parent = head.left;head.left.right.right = new Node(5);head.left.right.right.parent = head.left.right;head.right = new Node(9);head.right.parent = head;head.right.left = new Node(8);head.right.left.parent = head.right;head.right.left.left = new Node(7);head.right.left.left.parent = head.right.left;head.right.right = new Node(10);head.right.right.parent = head.right;Node test = head.left.left;System.out.println(test.value + " next: " + getSuccessorNode(test).value);test = head.left.left.right;System.out.println(test.value + " next: " + getSuccessorNode(test).value);test = head.left;System.out.println(test.value + " next: " + getSuccessorNode(test).value);test = head.left.right;System.out.println(test.value + " next: " + getSuccessorNode(test).value);test = head.left.right.right;System.out.println(test.value + " next: " + getSuccessorNode(test).value);test = head;System.out.println(test.value + " next: " + getSuccessorNode(test).value);test = head.right.left.left;System.out.println(test.value + " next: " + getSuccessorNode(test).value);test = head.right.left;System.out.println(test.value + " next: " + getSuccessorNode(test).value);test = head.right;System.out.println(test.value + " next: " + getSuccessorNode(test).value);test = head.right.right; // 10's next is nullSystem.out.println(test.value + " next: " + getSuccessorNode(test));}public static Node getSuccessorNode(Node node) {if(node==null)return null;Node cur=null;if(node.right!=null) {//有右孩子，则后继是右孩子的最左节点cur=node.right;while(cur.left!=null) {//注意循环终止条件，返回最后的没有左孩子的节点，而不是返回一个null节点！！cur=cur.left;}return cur;}else {//没有右孩子，向上找符合条件的父节点cur=node.parent;while(cur!=null&&node!=cur.left) {//注意条件！应先判断cur不为null,再判断node和cur.left的关系！不能反node=cur;cur=cur.parent;}			return cur;}}
}

运行结果：

3.4 找前驱节点

如果当前节点有左子树，则为左子树中最右的节点；

如果当前节点没有左子树，则：

• 当前节点通过parent指针找到父节点；
• 它是父节点的右孩子吗？
  • 不是，继续往上走；
  • 是，那前驱节点就为这个父节点。

4.二叉树的序列化和反序列化

记录一棵树的方式，以便后面可以恢复出来。

4.1 先序序列化

空节点用#表示

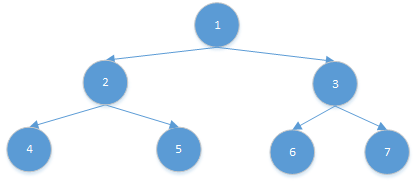
按先序遍历，得到一个字符串（节点之间用_连接）：

1_2_4_#_#_5_#_#_3_6_#_#_7_#_#

4.2 反序列化

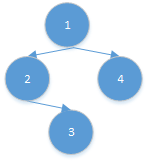
此树的先序序列化结果为：1_2_#_3_#_#_4_#_#

构建时，根据_，将字符串划分组，并放入队列中：

1、2、#、3、#、#、4、#、#

由于是先序遍历，最开始的1肯定是根；

2是1的左子树的根节点；

接着#表名，2左子树为空，则继续建2的右子树；

3为2的右子树的根节点；

#说明，3没有左子树；继续看3的右子树；

#表名3没有右子树；往上返：2的树建立完整，1还没有，继续1的右子树

接着的4是1右子树的根节点；

#表名，4没有左子树，接着建4的右子树；

#表名4没有右子树。

结束！

4.3 代码实现

public static String PreSeriaTree(Node root) {if(root==null)return "#_";String result=root.value+"_";result+=PreSeriaTree(root.left);result+=PreSeriaTree(root.right);return result;
}public static Node reconByPreString(String str) {String[] arr=str.split("_");Queue queue=new LinkedList();for(int i=0;i queue) {String value = queue.poll();if (value.equals("#")) {return null;}Node head = new Node(Integer.valueOf(value));head.left = reconPreOrder(queue);head.right = reconPreOrder(queue);return head;
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！