算法练习day13——190401(前缀树、贪心策略拼接字符串使字典序最小)
1.前缀树(Trie Tree)
1.1 字符串生成前缀树的过程
字母是填在路上的,不是填在节点上的。
首先是一个空的头结点:

加入“abc”到这棵树中:
头结点有到a的路吗?没有,添加:
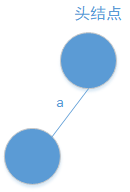
有a到b的路吗?没有,添加,c也一样:
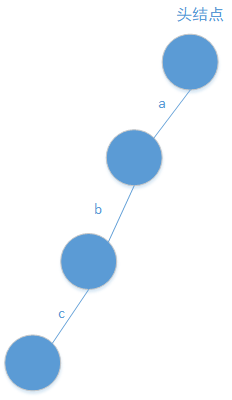
接着添加字符串“bce”:
添加字符串“abd”:
添加字符串“bef”:
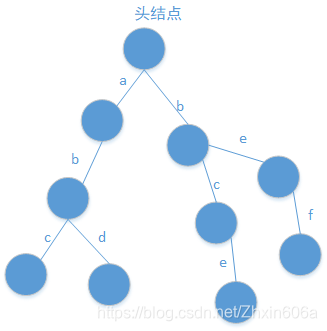
在添加N个字符串之后,可以查询,“某个字符串是否是以“be”开始的”。
若要查询“是否含有字符串“be”?”,原始的树结构,不足以实现这个功能。
- 添加了“bef”,但是“be”的路径和“bef”的路径是重合的,无法判断有没有加过“be”。
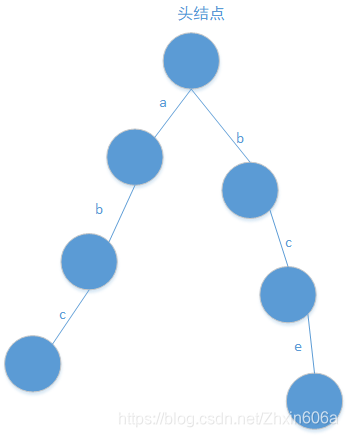
需在节点处添加一个值,表示有多少个字符串是以这个字符结尾的。更改之后的树结构如下图:
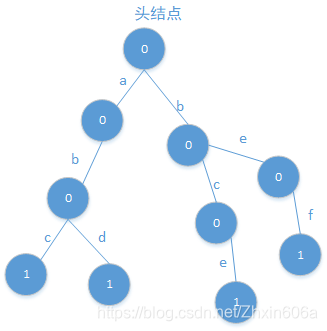
此时b-e中e后面的节点值为0,说明没有加过"be"。
此树结构还可以查某个字符串加过几次。
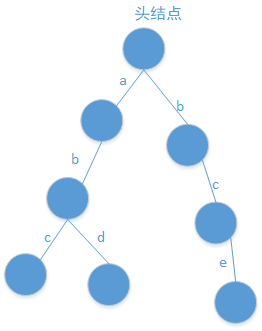
“给出有多少个字符串以给定的额字符串作为前缀”——需要再加一个数据项:每一个节点被划过了多少次。
上述树结构,更改之后如下图所示:
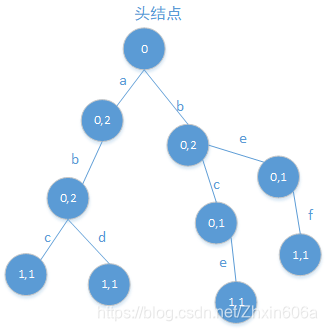
添加字符串的代价:字符串本身的长度,和数据量N无关;
查某个字符的代价:字符串本身的长度,和数据量N无关;
1.2 代码实现
package Tree;public class TrieTree {public static void main(String[] args) {Trie trie = new Trie();System.out.println(trie.search("hello"));trie.insert("hello");System.out.println(trie.search("hello"));trie.delete("hello");System.out.println(trie.search("hello"));trie.insert("hello");trie.insert("hello");trie.delete("hello");System.out.println(trie.search("hello"));trie.delete("hello");System.out.println(trie.search("hello"));trie.insert("helloa");trie.insert("helloac");trie.insert("helloab");trie.insert("helload");trie.delete("helloa");System.out.println(trie.search("helloa"));System.out.println(trie.prefixNumber("hello"));}public static class TrieNode{public int path;public int end;public TrieNode[] nexts;//此节点有多少条通往下层的路//通过判断此节点的路径指向的节点是否为空来判断这条路是否存在public TrieNode() {this.path=0;this.end=0;this.nexts=new TrieNode[26];//26个字母就26条路}}public static class Trie{TrieNode root;public Trie() {root=new TrieNode();}public void insert(String str) {if(str==null)return;char[] arr=str.toCharArray();TrieNode node=root;int index=0;for(int i=0;i运行结果:
2.贪心策略
(使用对数器严重贪心策略是否正确,不要纠结正确性证明)
贪心:根据某个标准分出个优先级,然后按照优先级的顺序执行。
2.1 举例
拼接字符串,使得结果为最小(按字典序)。
比如:"ab"、“cd”、"ef"三个字符串,拼接的结果可以由多种,但是”abcdef“这个结果才是最小的,题目中想要的。
2.1.1 分析
若先将字符串数组中的字符串拍好序再进行拼接,如下:
if(str1<=str2)str1连接str2;
elsestr2连接str1;
这种方式不对,因为:"b"<"ba",但是拼接之后"bba">"bab"。
所以正确的比较策略应该是:
if(str1连接str2<=str2连接str1)str1放前面;
elsestr2放前面;即,谁作为前缀更小谁放前面。
2.1.2 代码实现
package Solution;import java.util.Arrays;
import java.util.Comparator;public class StrCon {public static void main(String[] args) {String[] strs1 = { "jibw", "ji", "jp", "bw", "jibw" };System.out.println(lowestString(strs1));String[] strs2 = { "ba", "b" };System.out.println(lowestString(strs2));}public static class MyComparator implements Comparator{@Overridepublic int compare(String str1, String str2) {return (str1+str2).compareTo(str2+str1);/** compareTo* 如果指定的数与参数相等返回0。* 如果指定的数小于参数返回 -1。* 如果指定的数大于参数返回 1。*/} }public static String lowestString(String[] strs) {if(strs==null||strs.length==0)return " ";Arrays.sort(strs, new MyComparator());String res=" ";for(int i=0;i 运行结果:
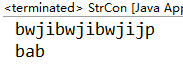
2.1.3 结论
当比较策略是个环时,不具有传递性,这个比较策略无效。
例如,有甲、乙、丙三个变量,订制的策略为:
- 甲和乙:甲在前;
- 乙和丙:乙在前;
- 甲和丙:丙在前。
以上策略构成一个环。
要使得比较的结果唯一,则设定的比较策略要具有传递性,即:
- a.b≤b.a
- b.c≤c.b
- 则:a.c≤c.a
以上式子中,将字符串等同于k进制的数:
连接
的结果为:
- 即12乘以10(进制)的21长度(2)次方
则字符串拼接可以理解为:
令,则上述的传递性规则可表示为:
化简:
由以上两个式子得:
由数的交换律和结合律可知:
所以:
化简结果:
得证。
要证明得到的字符串s是最小的字典序,即证明任意交换两个字符,得到的字典序都比s的字典序大。,
以得到的最小字典序字符串结果为:,要证明
肯定大于等于
在第一个串中,在
的前面,则:
若将和
交换:
一直换到和
挨着:
然后将b往前换:
最终:
所以,得到的结果已是最小。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!