1. 切金条

一块金条切成两半，是需要花费和长度数值一样的铜板的。

比如长度为20的金条， 不管切成长度多大的两半，都要花费20个铜板。

一群人想整分整块金条， 怎么分最省铜板？

例如，给定数组{10,20,30}， 代表一共三个人， 整块金条长度为10+20+30=60。金条要分成10，20，30三个部分。 如果， 先把长度60的金条分成10和50， 花费60。再把长度50的金条分成20和30，花费50。一共花费110铜板。但是如果先把长度60的金条分成30和30，花费60再把长度30金条分成10和20，花费30一共花费90铜板。

输入一个数组， 返回分割的最小代价。

1.1 分析

这是一个标准的哈夫曼问题：两个叶节点合并的时候，代价就是叶节点之和。

给定10，20，30，构成一个数，使得所有非叶节点之和最小。

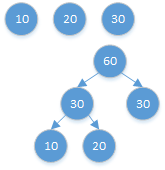
解题思路：

给定一组数：{1，2，6，4，3，7，1，8}，然后将这组数构成一个小根堆。每次从小根堆中拿出两个数。

第一次拿的肯定是两个1。这两个1生成一个节点，代价为2。然后把这个2扔回到小根堆中。

接着拿出两个数：两个2，这两个2合并的代价为4，然后将4扔回到小根堆中。。。。

最终得到的结果：

贪心：在所有的数中总是拿两个最小的。

此题中，切割的顺序是根据形成的树由上到下的。

1.2 代码实现

public static int lessMoney(int[] arr) {PriorityQueue pQ = new PriorityQueue<>();//系统实现的堆for (int i = 0; i < arr.length; i++) {pQ.add(arr[i]);//所有的数入堆}int sum = 0;int cur = 0;while (pQ.size() > 1) {//堆中元素只有一个时，停止cur = pQ.poll() + pQ.poll();//每次取两个，求和即为代价sum += cur;//当前和累加pQ.add(cur);//将和放回堆中}return sum;
}

2. 项目收益最大

输入：

• 参数1， 正数数组costs；
• 参数2， 正数数组profits；
• 参数3，正数k；
• 参数4， 正数w；
• costs[i]：表示i号项目的花费；
• profits[i]：表示i号项目在扣除花费之后还能挣到的钱(利润)；
• k表示你不能并行、 只能串行的最多做k个项目，即一次只能做一个项目，只能做够k个；
• w表示你初始的资金。

说明： 你每做完一个项目，马上获得的收益，可以支持你去做下一个项目。

输出： 你最后获得的最大钱数。

2.1 分析

将costs数组和profits数组合并为一个以项目为单位的数组：

[项目1（cost1,profit1），项目2（cost2,profit2）,...]

然后根据这个项目数组，建立一个小根堆，花费最小的在顶部。

在小根堆中，依次弹出花费小于w的头部。

将弹出的项目放入大根堆中，收益最大的在顶部。

然后选择大根堆顶部的项目执行，此项目一定是所有可做项目中收益最大的。

做完这个项目后，资金变多为w'（增加了此项目的收益），然后继续弹出小根堆中花费小于w'的头部，放到大根堆中，依收益排序。

这样一直做k个结束。

2.2 举例

2.3 代码实现

import java.util.Comparator;
import java.util.PriorityQueue;public class Code_03_IPO {public static class Node {//每个Node就是一个项目public int p;//收益public int c;//花费public Node(int p, int c) {this.p = p;this.c = c;}}public static class MinCostComparator implements Comparator {@Overridepublic int compare(Node o1, Node o2) {return o1.c - o2.c;}}public static class MaxProfitComparator implements Comparator {@Overridepublic int compare(Node o1, Node o2) {return o2.p - o1.p;}}public static int findMaximizedCapital(int k, int W, int[] Profits, int[] Capital) {Node[] nodes = new Node[Profits.length];for (int i = 0; i < Profits.length; i++) {//合并两个数组，以项目为单位重建一个数组nodes[i] = new Node(Profits[i], Capital[i]);}PriorityQueue minCostQ = new PriorityQueue<>(new MinCostComparator());//根据花费建立的小根堆PriorityQueue maxProfitQ = new PriorityQueue<>(new MaxProfitComparator());//根据收益建立的大根堆for (int i = 0; i < nodes.length; i++) {minCostQ.add(nodes[i]);//建小根堆}for (int i = 0; i < k; i++) {//项目数小于kwhile (!minCostQ.isEmpty() && minCostQ.peek().c <= W) {maxProfitQ.add(minCostQ.poll());//弹出堆顶花费小于已有资金的项目，加入大根堆中}if (maxProfitQ.isEmpty()) {return W;//大根堆为空，即没有可做的项目，返回总资金}W += maxProfitQ.poll().p;//执行大根堆堆顶的任务，增加总资金}return W;}
}

3.会议室安排

一些项目要占用一个会议室宣讲， 会议室不能同时容纳两个项目的宣讲。 给你每一个项目开始的时间和结束的时间(给你一个数组， 里面 是一个个具体的项目)， 你来安排宣讲的日程， 要求会议室进行的宣讲的场次最多。 返回这个最多的宣讲场次。

3.1 分析

贪心策略

1. 按开始时间安排，早就安排；——得不到最优解，有可能很早开始，然后占全天。
2. 按持续时间安排，持续时间短，安排它；——得不到最优解
   1. 
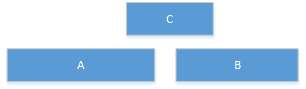
   2. C比A和B时间都短，但是安排了C，A和B都不能安排了。
3. 应该按照那个早结束来安排项目。
   1. 选择最早结束的项目；
   2. 淘汰掉因为做这个项目，而不能做的项目。
   3. 接着再选结束时间最早的项目，...。

3.2 代码实现

import java.util.Arrays;
import java.util.Comparator;public class BestArrange {public static class Program {public int start;public int end;public Program(int start, int end) {this.start = start;this.end = end;}}public static class ProgramComparator implements Comparator {@Overridepublic int compare(Program o1, Program o2) {return o1.end - o2.end;//结束时间早的安排在前面}}public static int bestArrange(Program[] programs, int start) {Arrays.sort(programs, new ProgramComparator());int result = 0;//完成的项目数for (int i = 0; i < programs.length; i++) {if (start <= programs[i].start) {//开始时间晚于给定的时间，则可以开始这个项目result++;start = programs[i].end;//将下一次开始时间设为当前已完成的项目结束时的时间}}return result;}
}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！