常用距离计算方法:

常用距离计算方法:
欧氏距离(欧几里得距离)
曼哈顿距离
闵可夫斯基距离
切比雪夫距离
余弦距离
距离计算
欧式距离
二维欧式距离公式如下：

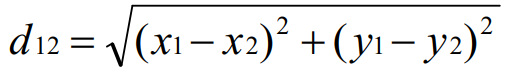
衍生三维欧式距离公式如下：

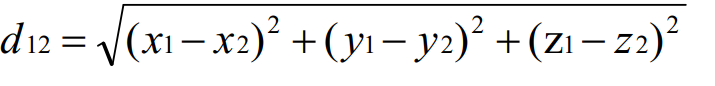
归纳N维欧式距离公式如下：

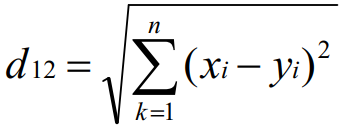
曼哈顿距离在几何空间中用的比较多。

二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离：

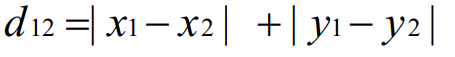
n维空间点(x11,x12,...,x1n)与b(x21,x22,...,x2n)的曼哈顿距离：

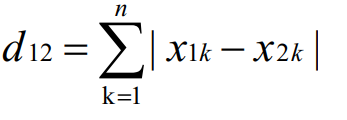
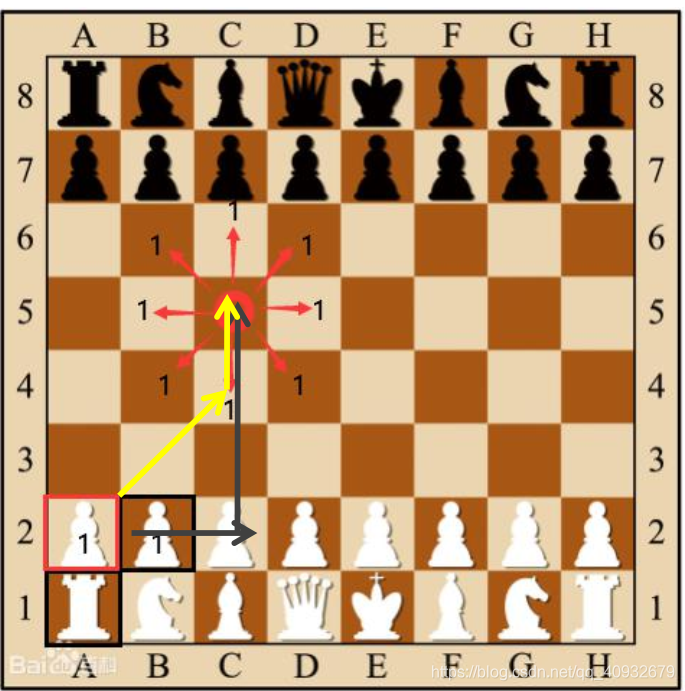
切比雪夫距离
在国际象棋中，国王可以直行、横行、斜行，所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步？这个距离就叫切比雪夫距离。

二维平面两点a(x1,x2)与b(x2,y2)间的切比雪夫距离：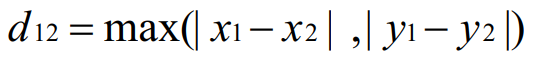

n维空间点a(x11,x12,...,x1n)与b(x21,x22,...,x2n)的切比雪夫距离：

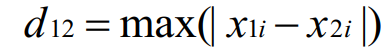
闵式距离是一类距离的统称，是对多个距离度量公式的概括性的表述。
两个n维变量a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的闵可夫斯基距离定义为：

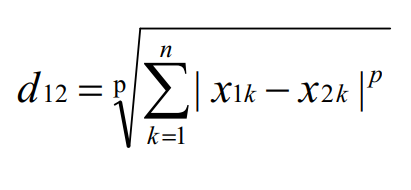
其中p是一个变参数：
u 当p=1时，就是曼哈顿距离；
u 当p=2时，就是欧氏距离；
u 当p→∞时，就是切比雪夫距离

 余弦距离实际上计算的是两个向量的夹角，是在方向上计算两者之间的差异，对绝对数值不敏感。

二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式：

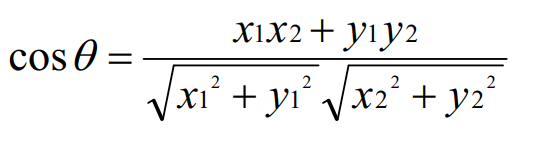
两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夹角余弦为：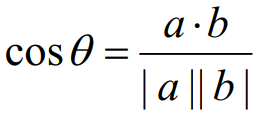
 

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！