图论

• 最小生成树
• 单源最短路
• 二分图

最小生成树

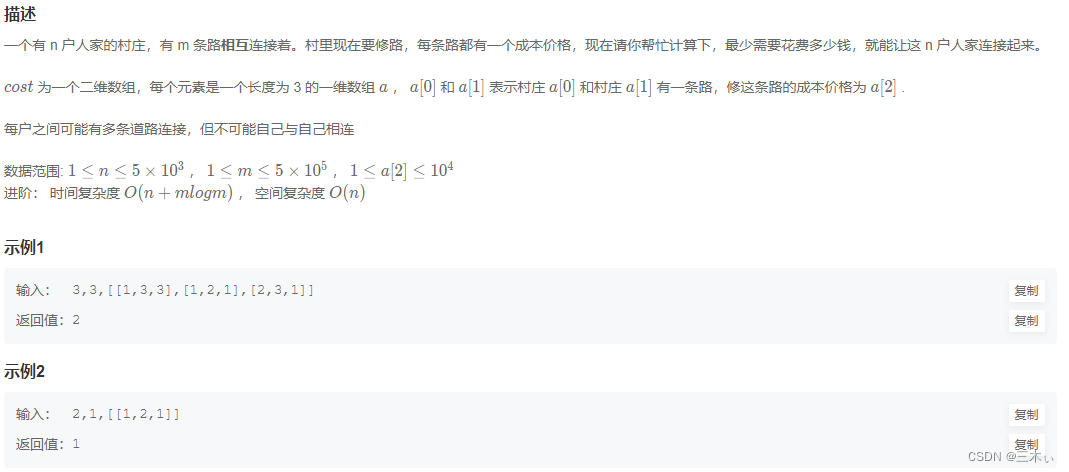
牛客连接： 最小生成树

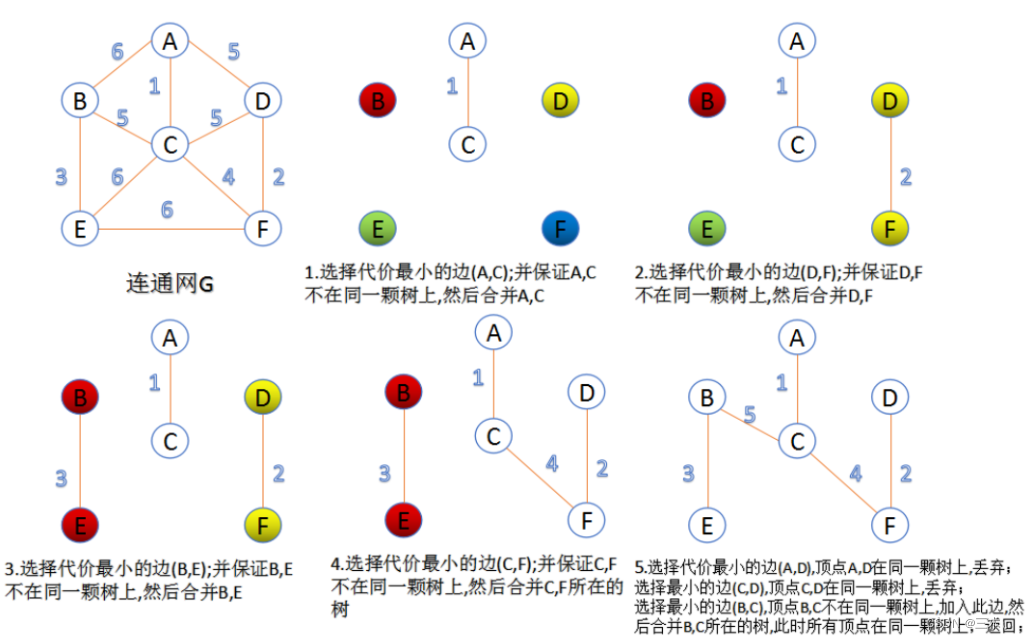
解法1
思路：kruskal算法+并查集

利用kruskal的思想，每次选择最短的路径，加入到候选集和中，从而最终连通整个图。
这里同时采用并查集的思想，每次将一条对一条候选路径进行选择的时候，判断两个端点是否拥有共同父亲，如果拥有则表明这两个点之间已经存在被加入候选集合中了，放弃这条边；如果没有拥有共同父亲，则将两个点连接，即指定一个点为另一个点的父亲，并且选择这条边加入连通图。最终，判断完所有的路径。

class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可** 返回最小的花费代价使得这n户人家连接起来* @param n int n户人家的村庄* @param m int m条路* @param cost intvector> 一维3个参数，表示连接1个村庄到另外1个村庄的花费的代价* @return int*/static bool comp(const vector<int >& x, const vector<int >& y){return x[2] < y[2];}int find_father(int &x, vector<int> &parents){return (parents[x] == x)?x:find_father(parents[x],parents);}    int miniSpanningTree(int n, int m, vector<vector<int> >& cost) {// write code heresort(cost.begin(),cost.end(),comp);int sum = 0;vector<int> parents(n+1);for(int i =0;i<=n;++i)         //建立并查集parents[i] = i;for(vector<int> i : cost){    //优先查找最路径int x = i[0];int y = i[1];int exp = i[2];x = find_father(x,parents);  //合并y = find_father(y,parents);if(x!=y){parents[x] = y;sum+=exp;}}return sum;}
};

解法2
思路：prim算法

#include 
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可** 返回最小的花费代价使得这n户人家连接起来* @param n int n户人家的村庄* @param m int m条路* @param cost intvector> 一维3个参数，表示连接1个村庄到另外1个村庄的花费的代价* @return int*/static bool comp(const vector<int> &x, const vector<int> &y){return x[2]<y[2];}int miniSpanningTree(int n, int m, vector<vector<int> >& cost) {// write code hereunordered_set<int> points;      //纳入确定集合sort(cost.begin(),cost.end(),comp);   //路径排序 保证优先查找到每个端点最短路径points.insert(cost[0][0]);			//最短路径两个端点先纳入集合points.insert(cost[0][1]);int res = cost[0][2];			cost.erase(cost.begin());while(true){                    //递归向外拓展最短路径if(points.size()==n)break;for(int i =0; i<cost.size(); ++i){   //一个端点在集合内一个端点不在集合内if((points.find(cost[i][0])!=points.end() && points.find(cost[i][1])==points.end()) || (points.find(cost[i][0])==points.end() && points.find(cost[i][1])!=points.end())){res+=cost[i][2];points.insert(cost[i][0]);points.insert(cost[i][1]);cost.erase(cost.begin()+i);break;}}}return res;}
};

单源最短路

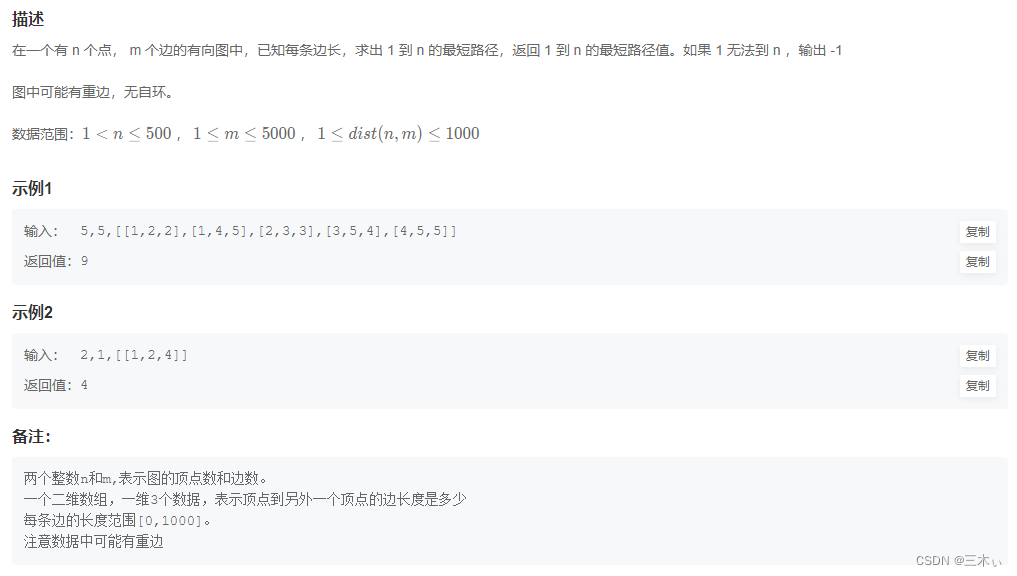
牛客链接:NC158 单源最短路

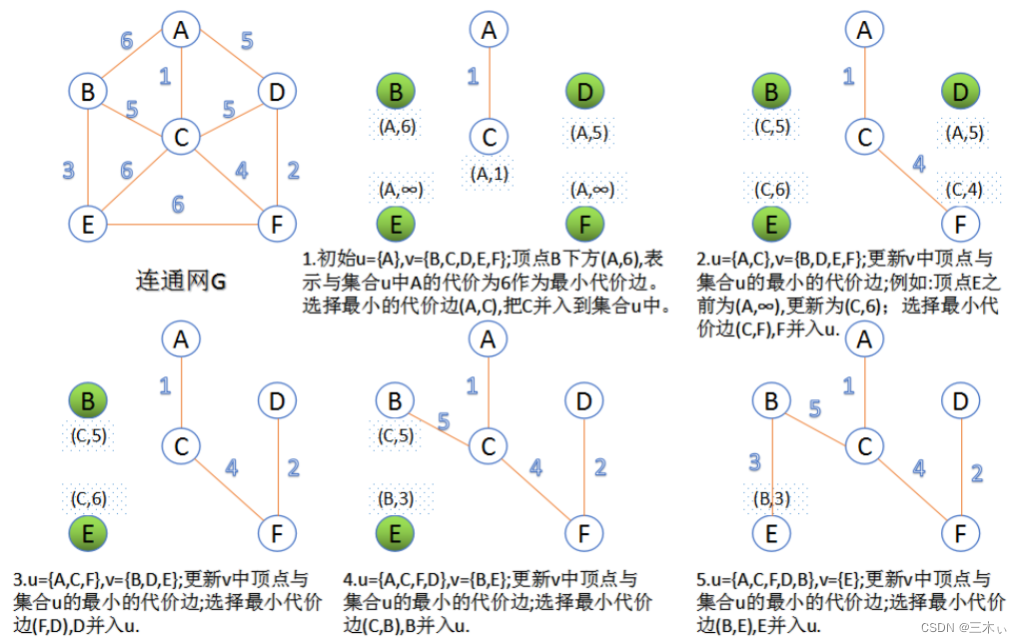
解法1：Dijkstra算法

每次确定一个最短距离，并且根据该最短距离，来更新能够从该点到达其他所有点的最短距离。

class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可** * @param n int 顶点数* @param m int 边数* @param graph intvector> 一维3个数据，表示顶点到另外一个顶点的边长度是多少​* @return int*/int dijkstra(vector> &matrix, int n){   vector vis(n+1, false);  //判断是否确认过最短距离vector dis(n+1,INT_MAX);    //用于迭代更新最短距离。dis[1] = 0;for(int i=1; i<=n;++i){int temp = -1;for(int j = 1;j<=n;++j){if(!vis[j] && (temp == -1 or dis[j] < dis[temp]))temp = j;}vis[temp] = true;for(int j = 1;j<=n;++j){if(matrix[temp][j] != INT_MAX && dis[temp] != INT_MAX)dis[j] = min(dis[j], dis[temp] + matrix[temp][j]);}}return dis[n];}int findShortestPath(int n, int m, vector >& graph) {// write code herevector> matrix(n+1,vector(n+1,INT_MAX));for(int i=1;i<=n;++i){matrix[i][i] = 0;}for(int i =0;i.size();++i){matrix[graph[i][0]][graph[i][1]] = min(matrix[graph[i][0]][graph[i][1]],graph[i][2]);}int ans = dijkstra(matrix,n);return ans==INT_MAX?-1:ans;}
};

二分图

力扣连接：剑指 Offer II 106.

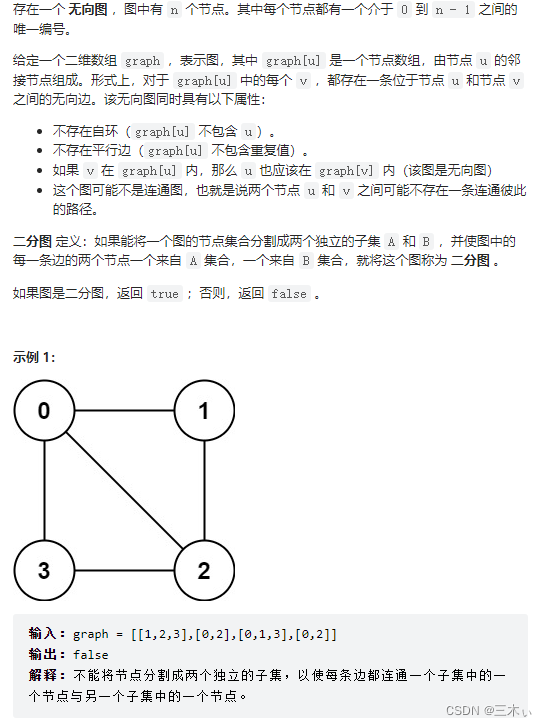
解法1：并查集

class Solution {
public:map<int,int> mp;int find_f(int a){  //用于分派，寻找到最终的祖先return mp[a]==a? a: find_f(mp[a]);}void union_nodes(int a, int b){  //合并两个节点，让其处于共同祖先mp[find_f(a)] = find_f(b);}bool isBipartite(vector<vector<int>>& graph) {for(int i = 0;i<graph.size();++i){  //集合初始化mp[i] = i;}for(int node = 0; node < graph.size(); ++node){for(int i=0; i<graph[node].size(); ++i){//如果有相邻节点的祖先和当前节点的祖先相同，则这两个是曾经被分配到同一组，则失败。if(find_f(node) == find_f(graph[node][i])) return false;union_nodes(graph[node][0],graph[node][i]); //将当前节点相邻节点和进行联合}}return true;}
};

解法2：dfs染色

对每个节点开始染色0，并沿着他的相邻节点依次染色为1，并对1的结点依次染色为0；过程中如果发现存在一个结点已经被染色，且他需要染的色和已经染的色不同，则错误。

class Solution {
public:bool setcolor(vector<vector<int>>& graph, vector<int>& color,int node, int color_need){if(color[node] != -1)    //只要被染过，就可以进行判断return color[node] == color_need;color[node] = color_need;for(auto i: graph[node]){if(!setcolor(graph,color,i,1-color_need)) //递归染色 1-color_need表示 0和1相互染return false;}return true;}bool isBipartite(vector<vector<int>>& graph) {vector<int> color(graph.size(),-1);for(int i=0;i<graph.size();++i){if(color[i] == -1){  //未染色的结点，加入染色并递归判断if(!setcolor(graph,color,i,0))return false;}}return true;}
};

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！