人工智能基础部分17-隐马尔科夫模型在序列问题的应用

大家好，我是微学AI，今天给大家介绍一下人工智能基础部分16-隐马尔科夫模型在序列问题的应用，隐马尔可夫模型(HMM)是一种统计模型，广泛应用于各种领域，如语音识别、自然语言处理、生物信息学等。本文将介绍隐马尔可夫模型的原理，并通过一个简单的生活中的例子提供完整的代码实现。

目录

一、隐马尔可夫模型简介

二、隐马尔可夫模型的三个基本问题

三、生活中的应用实例

四、代码实现与解析

五、总结

 一、隐马尔可夫模型简介

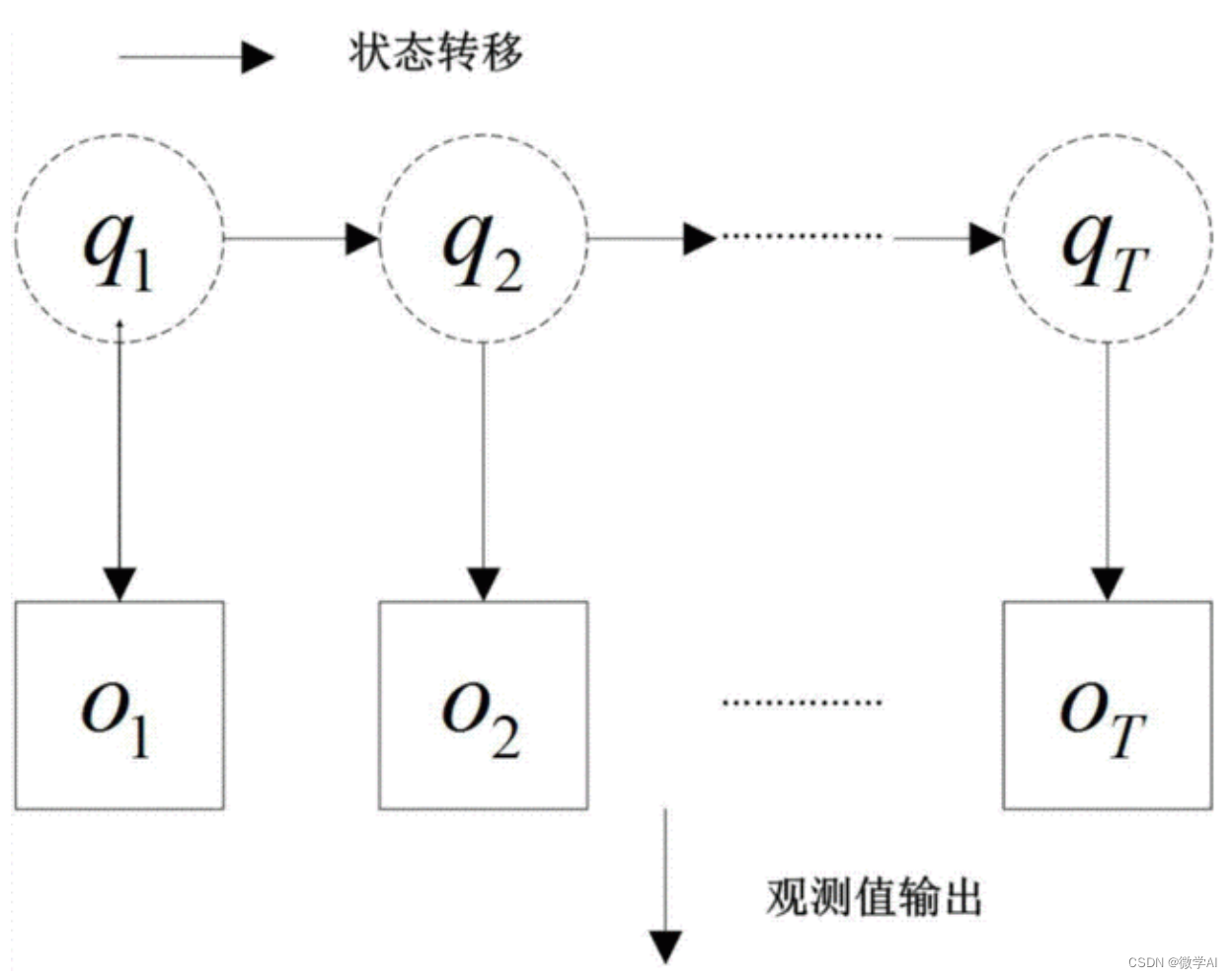
隐马尔可夫模型是一种具有隐藏状态的马尔可夫过程。在这个模型中，我们观察到的序列是由一个隐藏的马尔可夫链生成的。具体来说，隐马尔可夫模型由以下三部分组成：

状态序列：表示系统的内部状态，通常不可直接观察。

观测序列：根据状态序列生成的可观察到的序列。

参数：包括状态转移概率矩阵、观测概率矩阵和初始状态概率向量。

二、隐马尔可夫模型的三个基本问题

隐马尔可夫模型需要解决以下三个基本问题：

概率计算问题：给定模型参数和观测序列，计算该观测序列出现的概率。

学习问题：给定观测序列，估计模型的参数。

预测问题：给定观测序列和模型参数，找到最有可能的隐藏状态序列。

三、生活中的应用实例

假设有一个简化的天气系统，其中天气有两种状态：晴天（Sunny）和雨天（Rainy）。我们不能直接观察到天气，但是可以通过人们的穿着（例如戴太阳镜或雨伞）来间接地观察天气。我们将使用隐马尔可夫模型来描述这个系统，并通过给定的观测序列来预测天气状态。

四、代码实现与解析

本文通过使用Python实现的简单隐马尔可夫模型。代码实现了forward算法来计算观测序列的概率，viterbi算法来预测隐藏状态序列。

import numpy as npclass HiddenMarkovModel:def __init__(self, transition_matrix, observation_matrix, initial_prob):self.transition_matrix = transition_matrixself.observation_matrix = observation_matrixself.initial_prob = initial_probdef forward(self, observations):alpha = np.zeros((len(observations), len(self.initial_prob)))alpha[0] = self.initial_prob * self.observation_matrix[:, observations[0]]for t in range(1, len(observations)):alpha[t] = np.dot(alpha[t - 1], self.transition_matrix) * self.observation_matrix[:, observations[t]]return alpha, np.sum(alpha[-1])def viterbi(self, observations):path = np.zeros(len(observations), dtype=int)delta = np.zeros((len(observations), len(self.initial_prob)))psi = np.zeros((len(observations), len(self.initial_prob)))delta[0] = self.initial_prob * self.observation_matrix[:, observations[0]]for t in range(1, len(observations)):for j in range(len(self.initial_prob)):delta[t, j] = np.max(delta[t - 1] * self.transition_matrix[:, j]) * self.observation_matrix[j, observations[t]]psi[t, j] = np.argmax(delta[t - 1] * self.transition_matrix[:, j])path[-11] = np.argmax(delta[-1])for t in range(len(observations) - 2, -1, -1):path[t] = psi[t + 1, path[t + 1]]return pathif __name__ == "__main__":transition_matrix = np.array([[0.7, 0.3], [0.4, 0.6]])  # 状态转移矩阵observation_matrix = np.array([[0.9, 0.1], [0.2, 0.8]])  # 观测概率矩阵initial_prob = np.array([0.6, 0.4])  # 初始状态概率向量hmm = HiddenMarkovModel(transition_matrix, observation_matrix, initial_prob)observations = [0, 0, 1, 1, 0]  # 0代表戴太阳镜，1代表撑雨伞_, prob = hmm.forward(observations)print(f"观测序列概率：{prob:.4f}")hidden_states = hmm.viterbi(observations)print(f"最有可能的隐藏状态序列：{''.join(['S' if state == 0 else 'R' for state in hidden_states])}")

以上我定义了一个HiddenMarkovModel类，其中forward方法实现了前向算法计算观测序列的概率，viterbi方法实现了Viterbi算法来预测最有可能的隐藏状态序列。在__main__部分，我们生成了一个简化的天气系统的隐马尔可夫模型，并通过观测序列[0, 0, 1, 1, 0]（戴太阳镜、戴太阳镜、撑雨伞、撑雨伞、戴太阳镜）计算了观测序列的概率和最可能的天气状态序列。

五、总结

本文详细介绍了隐马尔可夫模型的原理，解决三个基本问题的方法，并通过一个简化的天气系统的例子提供了完整的代码实现。隐马尔可夫模型在许多实际应用中都有非常高的价值，如语音识别、自然语言处理等。希望本文能帮助大家更好地理解隐马尔可夫模型，并将其应用到实际问题中。

希望大家支持与关注哦。

往期作品：

 一、人工智能基础部分

1.人工智能基础部分1-人工智能的初步认识

2.人工智能基础部分2-一元一次函数感知器

3.人工智能基础部分3-方差损失函数的概念

4.人工智能基础部分4-梯度下降和反向传播

5.人工智能基础部分5-激活函数的概念

6.人工智能基础部分6-神经网络初步认识

7.人工智能基础部分7-高维空间的神经网络认识

8.人工智能基础部分8-深度学习框架keras入门案例

9.人工智能基础部分9-深度学习深入了解

10.人工智能基础部分10-卷积神经网络初步认识

11.人工智能基础部分11-图像识别实战

12.人工智能基础部分12-循环神经网络初步认识

13.人工智能基础部分13-LSTM网络：预测上证指数走势

14.人工智能基础部分14-蒙特卡洛方法在人工智能中的应用及其Python实现

15.人工智能基础部分15-自然语言处理中的数据处理上采样、下采样、负采样是什么？

16.人工智能基础部分16-神经网络与GPU加速训练的原理与应用

17.人工智能基础部分17-隐马尔科夫模型在序列问题的应用

18.人工智能基础部分18-条件随机场CRF模型的应用

...(待更新)

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！