目标优化算法 目标优化算法是一种通过迭代搜索来寻找最优解的方法。它的目标是在给定的限制条件下,最大化或最小化一个或多个目标函数。 以下是一些常见的目标优化算法: 1. 穷举法:将搜索空间中的每个可能的解都尝试一遍,找到最优解。适用于搜索空间较小的问题,但不适合大规模问题。 2. 单纯形法:一种常用的线性规划算法,通过移动一个多面体(称为单纯形)的顶点来逐步逼近最优解。 3. 遗传算法:模仿生物进化过程,通过选择、交叉和变异等操作,在解空间中进行搜索。适用于复杂的非线性问题。 4. 粒子群优化算法:模拟鸟群或鱼群等自然群体的行为,通过粒子在解空间中不断地迭代搜索最优解。 5. 模拟退火算法:模拟固体材料退火过程的行为,通过接受次优解的概率来避免陷入局部最优解。 6. 约束优化算法:考虑到问题可能存在一些约束条件,如等式约束或不等式约束,通过定义合适的惩罚函数或罚函数,将约束问题转化为无约束问题进行求解。 这些算法在不同的问题和应用领域中有不同的适用性,选择合适的算法需要根据具体问题的特点和要求进行评估和比较。 遗传算法: 遗传算法模拟生物进化的过程,通过选择、交叉和变异等操作来搜索最优解。 伪代码表示: 初始化种群 repeat 计算适应度 选择操作 交叉操作 变异操作 until 满足停止条件 输出最优解 这是一个简化版本的遗传算法的伪代码,实际实现中,种群的表示、适应度计算方法、选择策略、交叉方式和变异方式等细节都会有具体的实现方法。 粒子群优化算法: 粒子群优化算法模拟鸟群或鱼群等群体行为,通过粒子在解空间中的迭代搜索来寻找最优解。 伪代码表示: 初始化粒子群 repeat 更新粒子速度和位置 更新最优解 until 满足停止条件 输出最优解 这是一个简化版本的粒子群优化算法的伪代码,实际实现中,粒子表示、速度和位置更新策略、最优解更新策略等都会有具体的实现方法。 使用Python代码实现遗传算法和粒子群优化算法的简单示例: 遗传算法示例: import numpy as np# 定义目标函数
def objective_function(x):return x ** 2
# 定义适应度计算函数
def compute_fitness(population):return [objective_function(x) for x in population]
# 定义选择操作函数
def selection(population, fitness):fitness_normalized = fitness / np.sum(fitness)indices = np.random.choice(len(population), size=len(population), p=fitness_normalized)return [population[i] for i in indices]
# 定义交叉操作函数
def crossover(parent1, parent2):child = (parent1 + parent2) / 2return child
# 定义变异操作函数
def mutation(individual, mutation_rate):if np.random.rand() < mutation_rate:individual += np.random.uniform(-0.1, 0.1)return individual
# 初始化种群
population_size = 10
population = np.random.uniform(-10, 10, size=population_size)
mutation_rate = 0.2
num_generations = 100
# 遗传算法的主要迭代过程for generation in range(num_generations):
# 计算适应度
fitness = compute_fitness(population)# 选择操作
selected_population = selection(population, fitness)# 交叉操作
children = []
for i in range(population_size):parent1 = selected_population[np.random.randint(0, len(selected_population))]parent2 = selected_population[np.random.randint(0, len(selected_population))]child = crossover(parent1, parent2)children.append(child)# 变异操作
for i in range(population_size):children[i] = mutation(children[i], mutation_rate)# 更新种群
population = children
# 找到最优解
best_individual = population[np.argmin(fitness)]
best_fitness = np.min(fitness)
print("Best Individual:", best_individual)
print("Best Fitness:", best_fitness) 粒子群优化算法示例: import numpy as np# 定义目标函数
def objective_function(x):return x ** 2# 初始化粒子群
population_size = 10
num_dimensions = 1
population = np.random.uniform(-10, 10, size=(population_size, num_dimensions))
best_positions = population.copy()
best_fitness = np.array([objective_function(x) for x in population])
global_best_index = np.argmin(best_fitness)
global_best_position = population[global_best_index]
global_best_fitness = best_fitness[global_best_index]
velocity_range = (-0.5, 0.5)
inertia_weight = 0.7
cognitive_weight = 1.5
social_weight = 1.5
num_iterations = 100# 粒子群优化算法的主要迭代过程
for iteration in range(num_iterations):for i in range(population_size):# 更新速度velocity = (inertia_weight * population[i]+ cognitive_weight * np.random.rand() * (best_positions[i] - population[i])+ social_weight * np.random.rand() * (global_best_position - population[i]))velocity = np.clip(velocity, velocity_range[0], velocity_range[1])# 更新位置population[i] += velocity# 更新个体最优解fitness = objective_function(population[i])if fitness < best_fitness[i]:best_positions[i] = population[i]best_fitness[i] = fitness# 更新群体最优解if fitness < global_best_fitness:global_best_position = population[i]global_best_fitness = fitness# 找到最优解
best_individual = global_best_position
best_fitness = global_best_fitnessprint("Best Individual:", best_individual)
print("Best Fitness:", best_fitness) 这些示例代码都是简化的实现,仅提供了算法的基本框架。实际使用中,可能需要根据具体问题调整参数、选择适当的目标函数和约束条件,并进行更复杂的实现。正确的实现目标优化算法需要充分理解算法原理,并根据具体问题进行适当的调整和优化。 差分法 差分法是一种常用的数值计算方法,用于计算函数的导数或者构造差分方程。差分法基于函数在某一点附近的近似线性特性。通过计算函数在离该点一定距离处的函数值来近似计算导数的值。差分法的一般思路是利用有限差分逼近原函数的导数。常见的差分方法有前向差分、后向差分和中心差分等。前向差分使用函数值的前后两点之差来逼近导数值,后向差分使用函数值的后两点之差来逼近导数值,中心差分则使用函数值的前后两点之差的均值来逼近导数值。差分法在数值计算、数值模拟和数值求解微分方程等领域得到广泛应用。 差分法(Differential Evolution, DE)是一种基于种群的全局优化算法,常用于求解连续优化问题。它通过随机产生的变异向量与当前种群中的个体进行交叉,生成新的解向量,然后根据适应度函数进行选择,不断迭代以寻找最优解。 下面是差分法的简单实现示例: import numpy as np# 定义目标函数
def objective_function(x):return x ** 2
# 差分法算法
def differential_evolution(objective_function, bounds, population_size, max_generations, F, CR):num_dimensions = len(bounds)# 初始化种群population = np.random.uniform(bounds[:, 0], bounds[:, 1], size=(population_size, num_dimensions))for generation in range(max_generations):new_population = population.copy()for i in range(population_size):# 选择三个不同的个体作为变异向量candidates = [idx for idx in range(population_size) if idx != i]a, b, c = np.random.choice(candidates, size=3, replace=False)# 变异操作mutant = population[a] + F * (population[b] - population[c])# 交叉操作trial = np.where(np.random.rand(num_dimensions) <= CR, mutant, population[i])# 选择操作fitness_trial = objective_function(trial)fitness_current = objective_function(population[i])if fitness_trial < fitness_current:new_population[i] = trialpopulation = new_population# 找到最优解fitness_values = [objective_function(x) for x in population]best_individual = population[np.argmin(fitness_values)]best_fitness = np.min(fitness_values)return best_individual, best_fitness
# 设置问题的范围和参数
bounds = np.array([[-10, 10]])
population_size = 50
max_generations = 100
F = 0.8 # 缩放因子
CR = 0.9 # 交叉概率
# 使用差分法求解最优解
best_individual, best_fitness = differential_evolution(objective_function, bounds, population_size, max_generations, F,CR)
print("Best Individual:", best_individual)
print("Best Fitness:", best_fitness)在上述示例中, objective_function 函数表示优化问题的目标函数。 bounds 是问题的可行域范围, population_size 是种群规模, max_generations 是迭代的最大代数。 F 是缩放因子(用于调整变异向量的变化量), CR 是交叉概率(决定是否采用变异后的解向量)。最后,该示例通过调用 differential_evolution 函数来求解最优解。 需要注意的是,差分法算法的性能和结果可能会受到参数的影响,对于不同的问题和要求,可能需要调整和优化参数的设置。此外,较高的代数和种群规模可能会导致算法的计算量增大,因此需要根据具体问题的规模和计算资源进行适当的选择。 多目标优化 多目标优化是指在优化问题中存在多个相互独立的目标函数的情况。在多目标优化中,我们旨在找到一组解,使得在这组解中每个目标函数都能取得最佳的值,同时无法进一步改善一个目标函数的同时不损害其他目标函数。 以下是一些多目标优化中常见的数学公式和方法: Pareto 最优解: 在多目标优化中,Pareto 最优解是指找到一组解,其中没有其他解可以同时改善所有的目标函数。即无法通过改善一个目标函数而不损害其他目标函数。这样的解集称为 Pareto 最优解集。 Pareto 支配: 用于比较两个解的相对优劣程度的概念。解 A 支配解 B,当且仅当解 A 在所有目标函数上至少与解 B 相等,并且在至少一个目标函数上优于解 B。 Pareto 前沿(Pareto Front): Pareto 前沿是指所有不可被其他解支配的解组成的集合,即 Pareto 最优解集的边界。 多目标优化算法: 在多目标优化中,常用的算法包括多目标遗传算法(Multi-Objective Genetic Algorithm, MOGA),多目标粒子群优化算法(Multi-Objective Particle Swarm Optimization, MOPSO),多目标蚁群算法(Multi-Objective Ant Colony Optimization, MOACO)等等。这些算法通过利用种群的选择、交叉、变异等操作来逐步搜索 Pareto 前沿,从而得到多个最优解。 需要注意的是,多目标优化涉及到多个独立的目标函数,因此没有一个单一的公式可以涵盖所有情况。具体的数学公式和方法会因具体问题和所选算法而有所差异。以上提到的公式和方法只是多目标优化中的一些基本概念和常见算法,具体的数学公式和方法需要根据具体问题来选择和实施。 多目标优化(Multi-objective Optimization)是指在优化问题中存在多个冲突的目标函数,需要在不同目标之间找到最佳的平衡解。常用的多目标优化算法包括遗传算法、粒子群优化、差分进化算法等。 以下是一个使用遗传算法解决多目标优化问题的示例: import numpy as np# 定义目标函数(这里以多目标优化为例)
def objective_functions(x):# 假设有两个目标函数,需要最小化它们f1 = x[0]**2f2 = (x[0]-2)**2return np.array([f1, f2])# 初始化种群
def initialize_population(population_size, num_dimensions, bounds):population = np.random.uniform(bounds[0][0], bounds[0][1], size=(population_size, num_dimensions))return population# 遗传算法主函数
def genetic_algorithm(objective_functions, bounds, population_size, num_generations):num_dimensions = len(bounds[0])# 初始化种群population = initialize_population(population_size, num_dimensions, bounds)# 进化过程for generation in range(num_generations):fitness_values = np.array([objective_functions(x) for x in population])sorted_indices = np.lexsort((fitness_values[:, 0], fitness_values[:, 1]))sorted_population = population[sorted_indices]sorted_fitness_values = fitness_values[sorted_indices]best_individuals = sorted_population[:population_size]best_fitness = sorted_fitness_values[0]# 输出每一代的最佳结果print("Generation:", generation+1)print("Objective Values of Best Individuals:")for individual in best_individuals:print(objective_functions(individual))print("Best Fitness:", best_fitness)print("----------------------------------")# 选择、交叉和变异操作# 选择操作(这里省略具体实现)# 交叉操作(这里省略具体实现)# 变异操作(这里省略具体实现)return best_individuals, best_fitness# 设置参数
bounds = [(-10, 10)] # 决策变量范围
population_size = 50 # 种群大小
num_generations = 100 # 迭代次数# 运行遗传算法
best_individuals, best_fitness = genetic_algorithm(objective_functions, bounds, population_size, num_generations)在上述示例中, objective_functions 函数表示多目标优化问题的目标函数,返回一个包含多个目标函数值的列表。 bounds 是问题的可行域范围, population_size 是种群规模, num_generations 是迭代的最大代数。最后,通过调用 genetic_algorithm 函数来求解多目标优化问题的最优解。 这个示例使用了非支配排序和拥挤度计算来实现遗传算法中的选择操作,以维持多个非支配解并保持种群的多样性。每个目标函数都会产生一个帕累托前沿(Pareto front),通过将目标函数值排序并根据计算的拥挤度进行选择,可以非支配排序并保留一定数量的解作为最终的种群。 需要注意的是,多目标优化问题的求解需要考虑到解的多样性和平衡性,结果往往是一系列最优解的集合,而不是单个最优解。因此,除了最优解本身之外,还需要对整个帕累托前沿有所了解。 蒙特卡洛模型 蒙特卡洛模型是一种基于随机数和概率统计的数学模型,用于解决复杂问题和进行概率分析。它的基本原理是通过随机抽样和大量重复实验来估计和模拟系统的行为,以获取结果的近似解。蒙特卡洛模型通常具有以下特点: 随机抽样:蒙特卡洛模型使用随机数生成器来获得一系列随机样本,这些样本代表了问题的可能情况。随机抽样的方式能够覆盖全局解空间,并且每次抽样都是独立的。 大量重复实验:蒙特卡洛模型通过进行大量的重复实验来观察系统的行为,并根据这些实验结果进行统计分析。通过进行足够多的实验,可以逐渐减小估计误差,得到更准确的结果。 概率统计分析:蒙特卡洛模型使用统计分析方法来对实验结果进行处理,例如计算均值、方差、置信区间等。基于概率和统计的方法可以帮助在不确定的环境下进行决策和预测。 蒙特卡洛模型在各个领域都有广泛的应用,例如金融风险评估、物理模拟、优化问题求解、统计建模、游戏理论等。它可以处理复杂的问题,不受维度和非线性影响,并能提供近似解的置信度。 总结起来,蒙特卡洛模型是基于随机抽样和概率统计的数学模型,通过大量的重复实验来估计和模拟系统的行为,用于解决复杂问题和进行概率分析。 蒙特卡洛模型(Monte Carlo model)是一种基于随机模拟和概率统计的数学模型,用于解决复杂问题和进行数值计算。它以蒙特卡洛赌场为名,源自于随机游戏的概率计算方法。 蒙特卡洛模型的基本思想是通过生成大量的随机样本,并基于这些样本进行统计分析,得出问题的解或结果的近似值。它适用于无法通过解析方法求解的问题,或者通过解析方法求解非常困难的问题。 蒙特卡洛模型通常包括以下步骤: 定义问题:明确问题的目标和约束条件。 建立模型:将问题转化为数学模型,确定模型的输入和输出。 随机抽样:生成大量符合输入分布的随机样本。这可以使用伪随机数生成器来实现。 模拟运行:基于随机样本,运行模型或模拟实验,并得出输出结果。 统计分析:对输出结果进行统计分析,如计算均值、方差、置信区间等。 结果解释:根据统计分析结果,得出问题的解或结果的近似值,并进行解释和验证。 蒙特卡洛模型可以应用于各种领域和问题,如金融风险评估、粒子物理学实验、工程优化、交通规划等。它的优点是可以处理复杂的非线性问题,不需要求解复杂的数学方程,且可以提供对结果的不确定性估计。然而,蒙特卡洛模型通常需要大量的随机样本才能得到准确的结果,因此计算效率可能较低。 总之,蒙特卡洛模型是一种基于随机模拟和概率统计的数学模型,通过生成大量的随机样本并进行统计分析,用于解决复杂问题和进行数值计算。 当使用Python实现蒙特卡洛模型时,我们需要考虑问题的具体情况和模型的输入输出。下面是一个简单的示例,用Python代码实现在单位正方形内估算π的值: import random
def estimate_pi(num_samples):num_inside = 0for _ in range(num_samples):x = random.uniform(0, 1)y = random.uniform(0, 1)if x**2 + y**2 <= 1:num_inside += 1pi_estimate = 4 * (num_inside / num_samples)return pi_estimate
# 估算π的值
num_samples = 1000000
pi_estimate = estimate_pi(num_samples)
print("Estimated value of pi:", pi_estimate)在上述示例中, estimate_pi 函数接受一个参数 num_samples ,表示在正方形内随机生成的点数量。通过生成随机点并计算落在单位圆内的点的比例,最后乘以4得到π的估计值。调用 estimate_pi 函数并传入所需的样本数量,即可获得对π值的估计。 需要注意的是,蒙特卡洛模型的准确性和可靠性与样本数量有关,样本数量越大,结果越接近真实值。在实际应用中,可能需要根据问题的要求和计算资源进行适当的样本数量选择。 这只是一个简单的示例,蒙特卡洛模型的应用非常广泛,具体的实现方式会因问题的不同而有所差异。可以根据具体问题的要求和模型的输入输出设计代码实现。 主成分分析(Principal Component Analysis,PCA)是一种常用的降维技术和数据分析方法。它通过线性变换将高维数据映射到低维空间中,以发现数据中的关键特征或主要变化方向。 主成分分析的基本思想是将原始数据投影到一个新的正交特征空间,使得投影后的特征具有最大的方差。这些投影后的特征被称为主成分,按照方差递减的顺序排序,第一个主成分具有最大的方差,第二个主成分具有次大的方差,以此类推。 下面是主成分分析的一些数学计算步骤: 标准化: 如果原始数据的不同特征具有不同的单位和范围,我们首先需要对数据进行标准化,使得每个特征具有零均值和单位方差,以便消除量纲的影响。 协方差矩阵计算: 根据标准化后的数据,计算特征之间的协方差矩阵。协方差矩阵反映了特征之间的线性相关性。 特征值分解: 对协方差矩阵进行特征值分解,得到特征值和对应的特征向量。特征向量代表了数据在新特征空间中的方向,特征值表示每个特征向量方向上的方差。 主成分选择: 根据特征值的大小,按照降序排列选择最大的 k 个特征值对应的特征向量,这些特征向量构成了新的特征空间的基,称为主成分。 数据投影: 将原始数据通过主成分的线性组合,将其投影到新的特征空间上,得到降维后的数据表示。 主成分分析结果可以用于数据可视化、特征选择、数据压缩、去除噪声等应用。通过选择适当数量的主成分,我们可以在保留较高的信息量的情况下,实现数据的降维和简化,从而有助于更好地理解和分析数据。需要注意的是,选择主成分的数量需要根据具体问题和实际需求来确定。 下面是使用Python中的 scikit-learn 库来实现主成分分析的简单示例: from sklearn.decomposition import PCA
import numpy as np
# 创建一个例子数据集
X = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]])
# 初始化PCA对象
pca = PCA(n_components=2)
# 执行主成分分析
X_transformed = pca.fit_transform(X)
# 输出降维后的数据
print("Transformed Data:\n", X_transformed)在上述示例中,我们首先创建了一个简单的数据集X,其中包含4个样本,每个样本具有3个特征。然后,我们初始化了一个PCA对象,指定希望降维后的特征数量为2(即将数据从3维降到2维)。最后,我们调用 fit_transform 方法对数据集进行主成分分析并得到降维后的数据X_transformed。 请注意,这只是主成分分析的一个简单示例,实际应用中可能涉及更复杂的数据集和参数调整。同时,需要根据具体的应用场景和数据特性来选择合适的主成分个数和分析方法。 除了降维和特征提取之外,主成分分析还可以用于数据可视化、异常检测等任务,是一项非常有用的数据分析工具。深入了解主成分分析的理论和应用可以帮助更好地应用该技术。 层次分析(Analytic Hierarchy Process,AHP)是一种用于分析和决策的多准则决策方法。它将问题分解为不同层级(层次),并根据各层级中准则或因素之间的相对重要性进行评价和权重分配,以支持决策者做出决策。 层次分析的基本步骤如下: 建立层次结构: 将复杂的决策问题层次化,分为目标层、准则层和方案层。目标层是最高层,代表决策的最终目标;准则层包括一组评判标准或因素,用于评估方案的优劣;方案层包括一组可选方案。 构建判断矩阵: 在准则层中,对每个准则两两比较,判断其相对重要性。通过判断矩阵,将比较转化为数值方式。判断矩阵的元素代表两个准则的相对重要性比例,比如:准则 A 相对于准则 B 的重要性为 3。 计算权重: 根据判断矩阵,计算每个准则的权重。常用的计算方法是特征向量法,将判断矩阵的特征向量标准化后,作为准则权重。 一致性检验: 根据判断矩阵的一致性检验,判断判断矩阵的一致性程度。如果一致性是满足的,则可继续进行下一步。如果不满足一致性,则需要重新调整判断矩阵。 方案评估: 在方案层,将每个方案与准则进行对比评估,得到每个方案相对于每个准则的得分或权重。 综合评价与决策: 根据准则权重和方案评估,综合计算每个方案的综合得分,进行排名或选取最优方案。 层次分析方法通过将问题分解为多个层次,并通过定量分析和主观评估,支持决策者进行准则权重的分配和方案评估,以帮助做出合理的决策。它广泛应用于各个领域,如决策分析、项目评估、供应链管理、投资决策等 from numpy import matrix
from scipy.linalg import eig
# 输入判断矩阵
matrix_values = [[1, 2, 4],[1/2, 1, 1/2],[1/4, 2, 1]]
# 标准化判断矩阵
normalized_matrix = matrix(matrix_values) / matrix(matrix_values).sum(axis=0)
# 计算特征向量和特征值
eigenvalues, eigenvectors = eig(normalized_matrix)
# 通过最大特征值找到权重向量
max_eigenvalue_index = eigenvalues.argmax()
weights = eigenvectors[:, max_eigenvalue_index].real
normalized_weights = weights / weights.sum()
# 输出权重向量
print("Normalized weights:", normalized_weights)在上述示例中,我们首先定义了一个判断矩阵 matrix_values ,其中包含了对不同准则或方案之间的相对重要性进行判断的数据。然后,我们对判断矩阵进行标准化,以确保每一列的和为1。接下来,我们使用特征值分解方法计算特征向量和特征值,并选择最大特征值对应的特征向量作为权重向量。最后,我们将权重向量进行归一化,以得到最终的权重值。 需要注意的是,层次分析的实现可以使用不同的工具和软件,上述示例仅仅演示了如何通过基本的数学运算来计算权重向量。在实际应用中,可能还需要考虑其他因素,如一致性检验和专家判断信息的融入。 总之,层次分析是一种用于多准则决策问题的定量分析方法,通过对判断矩阵进行标准化、特征值分解和归一化等步骤,可以得出不同准则和选择的权重向量。这样的权重信息可以帮助决策者做出更有根据的决策。 模糊综合评价是一种基于模糊逻辑的多准则决策方法,用于处理评估过程中存在的不确定性和模糊性。它可以将多个评价指标综合考虑,得出一个综合评价结果。 模糊综合评价的基本步骤如下: 确定评价指标: 首先,确定用于评价的指标,这些指标可以是定量指标或定性指标。每个指标都代表了问题的一个方面。 构建模糊评价集合: 对于每个评价指标,根据实际情况构建相应的模糊评价集合。模糊评价集合由隶属度函数表示,用来描述指标的程度或类别。 设定模糊评价规则: 根据具体情况,制定模糊评价规则,规定各个指标之间的权重和关联关系。这些规则可以基于专家经验、统计数据或其他信息。 计算模糊评价集合的隶属度: 对于每个指标,计算其模糊评价集合的隶属度,表示该指标在不同程度上符合相应的模糊评价。 进行模糊逻辑运算: 使用模糊逻辑运算,如模糊交、模糊并、模糊加权平均等,将各个指标的隶属度进行组合,得到综合评价结果。 解模糊化: 使用解模糊化方法,将模糊的综合评价结果转化为确定的评价值。常用的解模糊化方法有重心法、面积法、平均最大值法等。 最终得到的综合评价结果可以用于进行决策、比较不同方案或做出优先级排序。模糊综合评价方法在复杂的决策问题中广泛应用,特别适用于评估问题具有模糊性、不确定性和主观性的情况下。需要根据具体问题和实际需求选择合适的模糊综合评价方法和技术。 模糊综合评价(Fuzzy Comprehensive Evaluation)是一种基于模糊理论的多准则决策方法,用于评估和排序多个因素对某一目标的贡献程度。它考虑到了不同因素之间的相互关联和不确定性,并通过对模糊集合的运算进行综合评估。 下面是一个简单的示例,演示如何使用模糊综合评价方法进行决策: import numpy as np
# 定义评价指标的模糊关系矩阵
relationship_matrix = np.array([[1, 0.3, 0.5],[0.3, 1, 0.7],[0.5, 0.7, 1]])
# 定义权重向量
weights = np.array([0.4, 0.3, 0.3])
# 进行模糊综合评价
result = np.dot(relationship_matrix, weights)
# 输出评估结果
print("Evaluation result:", result)在上述示例中,我们首先定义了评价指标的模糊关系矩阵 relationship_matrix ,该矩阵表示各个评价指标之间的关联程度。然后,我们定义了权重向量 weights ,其中的权重值表示各个评价指标的重要程度。通过使用矩阵乘法运算,我们对模糊关系矩阵和权重向量进行运算,得到最终的评估结果。 需要注意的是,在实际应用中,模糊综合评价方法可能会涉及更复杂的模糊集合运算和权重确定的过程。同时,可能需要考虑到一些专家知识和经验,对不同指标和关系进行适当的建模和调整。 总之,模糊综合评价是一种基于模糊理论的多准则决策方法,通过对模糊关系矩阵和权重向量进行运算,对不确定和模糊的评价指标进行综合评估和排序,从而帮助决策者做出更科学有效的决策。 目标规划优化是一种优化方法,用于在具有多个目标和多个约束条件的问题中找到最优解。与传统的单目标优化方法相比,目标规划优化考虑了多个目标之间的权衡和约束条件的限制。 目标规划优化的基本步骤如下: 确定决策变量: 首先,确定参与决策的变量,这些变量可以是决策问题的各个方面或参数。 确立目标函数: 对于每个要优化的目标,构建相应的目标函数。每个目标函数可以代表问题的一个方面,并给定其优化的目标。 确定约束条件: 根据问题的限制条件,确定相应的约束条件。约束条件可以是线性方程、线性不等式、非线性方程等,限制了决策变量的取值范围。 设计优化模型: 将目标函数和约束条件结合起来,建立目标规划优化模型。模型可以是线性规划、整数规划、非线性规划等。 求解最优解: 使用相应的优化算法,求解目标规划优化模型,找到使目标函数最优的决策变量组合。 解释和分析结果: 解释最优解的含义和影响,对优化结果进行分析。根据实际需求和问题背景,进行结果的解释和决策。 目标规划优化方法可以应用于各个领域,如供应链优化、资源分配、生产计划等。它可以同时考虑多个目标的权衡,并在约束条件下找到最优解。需要根据具体问题和实际需求选择合适的目标规划优化方法和算法。 目标规划优化是一种数学建模和优化方法,用于解决多目标决策问题。它旨在在满足一组限制条件的前提下,找到一组最优的决策变量值,以最大化或最小化多个目标函数。 以下是一个简单的示例,演示如何使用目标规划优化方法: from scipy.optimize import minimize
# 定义目标函数
def objective(x):return 2*x[0]**2 + 3*x[1]**2 + 4*x[2]**2 + 5*x[3]**2
# 定义限制条件函数
def constraint1(x):return x[0] + x[1] + x[2] + x[3] - 10
def constraint2(x):return x[0] - x[1] + 2*x[2] - x[3] - 5
# 定义初始值
x0 = [0, 0, 0, 0]
# 定义限制条件
constraint_eq = [{'type': 'eq', 'fun': constraint1},{'type': 'eq', 'fun': constraint2}]
# 执行目标规划优化
result = minimize(objective, x0, method='SLSQP', constraints=constraint_eq)
# 输出最优解和最优值
print("Optimal solution:", result.x)
print("Optimal value:", result.fun)在上述示例中,我们首先定义了一个目标函数 objective ,其中包含了需要最大化或最小化的多个目标函数。然后,我们定义了一些限制条件函数,用于约束决策变量的取值范围。接着,我们指定了初始值 x0 和限制条件 constraint_eq ,并使用 minimize 函数执行目标规划优化。 需要注意的是,上述示例中使用了 scipy 库中的 minimize 函数,方法选择了 SLSQP (Sequential Least Squares Programming)作为优化算法,同时通过 constraints 参数传入了限制条件。在实际应用中,根据问题的特性和需求,可能需要选择不同的优化算法和添加其他类型的限制条件。 目标规划优化方法可以用于各种多目标决策问题,如资源分配、生产计划、投资组合等。它能够帮助决策者在面临多个目标和限制条件时做出更优的决策。 群智能算法 群智能算法(Swarm Intelligence Algorithms)是一类基于群体行为和协作思想的优化算法。这些算法模拟了群体中个体之间的相互作用和信息交流,在解决复杂优化问题方面表现出良好的性能。 以下是几种常见的群智能算法: 粒子群优化算法(Particle Swarm Optimization, PSO): PSO模拟了鸟群或鱼群在搜索空间中的搜寻行为。每个粒子代表一个潜在解,在搜索过程中通过学习自身和邻域最优解来更新自身的位置和速度,以逐步搜索到全局最优解。 蚁群算法(Ant Colony Optimization, ACO): ACO模拟了蚂蚁在寻找食物和建立路径时的行为。蚂蚁通过释放信息素并根据信息素浓度和距离选择路径,集体协作找到最短路径或优化解。 人工鱼群算法(Artificial Fish Swarm Algorithm, AFSA): AFSA模拟了鱼群中鱼的觅食行为。每条人工鱼在搜索过程中通过模拟觅食、觅食竞争和觅食追随等策略,集体协作优化问题并找到全局最优解。 群体智能优化算法(Swarm Intelligence Optimization, SIO): SIO是一种综合性的群智能算法框架,包括基于领导者-跟随者行为、奇点搜索等策略的不同子算法。这些子算法可以根据具体问题选择和组合,进行多方面的优化和搜索。 群智能算法通过个体之间的协作和信息交流,以群体的智慧和集体的行为优势来解决复杂的优化问题。它们通常具有强大的全局搜索能力和鲁棒性,适用于多种问题领域,如优化、机器学习、图像处理等。需要根据具体问题的特点选择合适的算法,并进行参数调节和优化。 下面是使用Python展示粒子群优化(Particle Swarm Optimization,PSO)算法的简单示例代码: import numpy as np
# 定义目标函数
def objective_function(x):return sum(x**2)
# 定义粒子群优化算法
def particle_swarm_optimization(objective_func, num_particles, num_dimensions, num_iterations):# 设置参数inertia_weight = 0.9 # 惯性权重cognitive_weight = 2 # 认知权重social_weight = 2 # 社会权重max_velocity = 0.5 # 最大速度lower_bound = -5 # 变量下界upper_bound = 5 # 变量上界# 初始化粒子位置和速度particle_positions = np.random.uniform(lower_bound, upper_bound, (num_particles, num_dimensions))particle_velocities = np.random.uniform(-max_velocity, max_velocity, (num_particles, num_dimensions))particle_best_positions = particle_positions.copy()global_best_position = particle_best_positions[np.argmin([objective_func(p) for p in particle_best_positions])]# 迭代优化for _ in range(num_iterations):for i in range(num_particles):# 更新速度r1 = np.random.rand()r2 = np.random.rand()cognitive_velocity = cognitive_weight * r1 * (particle_best_positions[i] - particle_positions[i])social_velocity = social_weight * r2 * (global_best_position - particle_positions[i])particle_velocities[i] = inertia_weight * particle_velocities[i] + cognitive_velocity + social_velocity# 限制速度范围particle_velocities[i] = np.maximum(np.minimum(particle_velocities[i], max_velocity), -max_velocity)# 更新位置particle_positions[i] += particle_velocities[i]particle_positions[i] = np.maximum(np.minimum(particle_positions[i], upper_bound), lower_bound)# 更新个体最优解和全局最优解if objective_func(particle_positions[i]) < objective_func(particle_best_positions[i]):particle_best_positions[i] = particle_positions[i]if objective_func(particle_positions[i]) < objective_func(global_best_position):global_best_position = particle_positions[i]return global_best_position
# 设置随机种子,保证结果可重现性
np.random.seed(0)
# 运行粒子群优化算法
best_solution = particle_swarm_optimization(objective_function, num_particles=50, num_dimensions=2, num_iterations=1000)
# 输出最优解和最优值
print("Optimal solution:", best_solution)
print("Optimal value:", objective_function(best_solution))上述代码中,首先定义了一个简单的目标函数 objective_function ,它计算输入向量的每个维度平方的和。然后,实现了粒子群优化算法 particle_swarm_optimization ,其中设置了适当的参数(惯性权重、认知权重、社会权重、最大速度等),并进行初始化和迭代优化过程。在主程序中,使用设定好的参数运行粒子群优化算法,并输出最优解和最优值。 需要注意的是,在实际应用中,可能需要根据具体问题和需求进行适当的参数调整,并对目标函数和约束条件进行适当的修改。此外,粒子群优化算法还有其他版本和变种,如改进的粒子群优化算法(Improved Particle Swarm Optimization,IPSO)和并行粒子群优化算法(Parallel Particle Swarm Optimization,PPSO),可以根据实际情况进行选择和应用。 动态规划 动态规划是一种常见的优化问题求解方法,特别适用于具有重叠子问题和最优子结构性质的问题。它将一个复杂的问题分解为多个子问题,并通过保存并重复使用子问题的解来避免重复计算,从而提高求解效率。 动态规划通常包含以下步骤: 定义状态: 将原问题划分为若干个子问题,并定义与子问题相关的状态。状态是问题中变化的部分,它可以用来描述问题的特征和变化过程。 定义状态转移方程: 设计状态之间的转移关系,即从一个状态到另一个状态的转移过程。状态转移方程通常使用递推关系来描述子问题与原问题的联系,并可以通过已知的子问题解来计算当前问题的解。 确定边界条件: 根据问题的特点,确定最简单的子问题的解,即边界条件。边界条件是递归终止条件,它们提供了从子问题向上求解的基础。 计算最优解: 根据状态转移方程和边界条件,利用自底向上的方式计算各个子问题的最优解,并最终得到原问题的最优解。 动态规划可以应用于各种具有最优子结构性质的问题,如最短路径问题、背包问题、序列比对问题等。通过合理地定义状态和状态转移方程,并使用适当的数据结构和算法,可以高效地求解复杂优化问题。 需要注意的是,动态规划算法需要一定的内存空间来存储子问题的解,而且在状态数量较多时可能导致计算复杂度较高。因此,在应用动态规划时,需要权衡时间与空间的利用,根据具体问题的规模和特点选择合适的求解方法和数据结构。 下面是一个用 Python 实现动态规划的简单示例代码,以计算斐波那契数列中第 n 个数为例: # 使用动态规划计算斐波那契数列
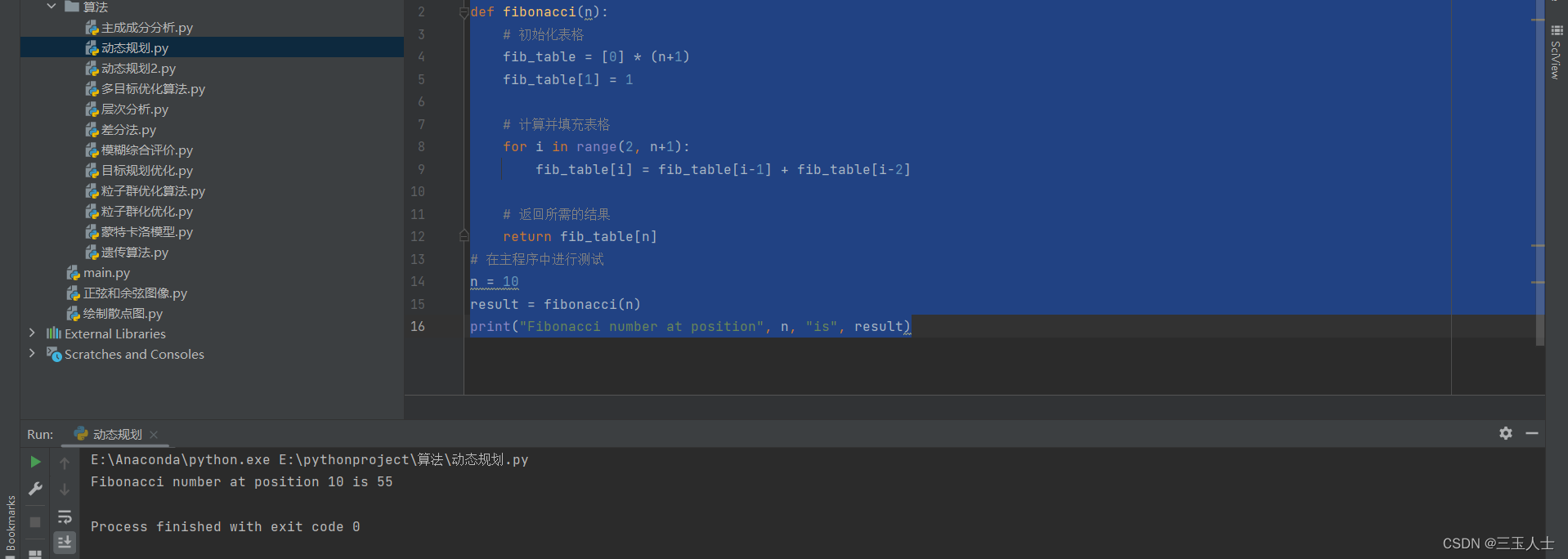
def fibonacci(n):# 初始化表格fib_table = [0] * (n+1)fib_table[1] = 1# 计算并填充表格for i in range(2, n+1):fib_table[i] = fib_table[i-1] + fib_table[i-2]# 返回所需的结果return fib_table[n]
# 在主程序中进行测试
n = 10
result = fibonacci(n)
print("Fibonacci number at position", n, "is", result)上述代码使用动态规划的思想计算斐波那契数列中第 n 个数。它首先创建一个长度为 (n+1) 的列表 fib_table ,用于记录不同位置的斐波那契数值。然后,它通过迭代计算并填充表格,根据递推关系式 fib_table[i] = fib_table[i-1] + fib_table[i-2] ,依次计算出斐波那契数列中的每个值。最后,返回第 n 个数作为结果。 在实际应用中,动态规划可用于解决各种问题,如最短路径问题、背包问题、序列对齐等。需要注意的是,不同的问题可能需要不同的状态定义和递推关系,因此在解决具体问题时需要根据问题的特性进行适当的调整和定制编写代码。 使用动态规划解决背包问题的示例代码: # 使用动态规划解决# 使用动态规划解决背包问题
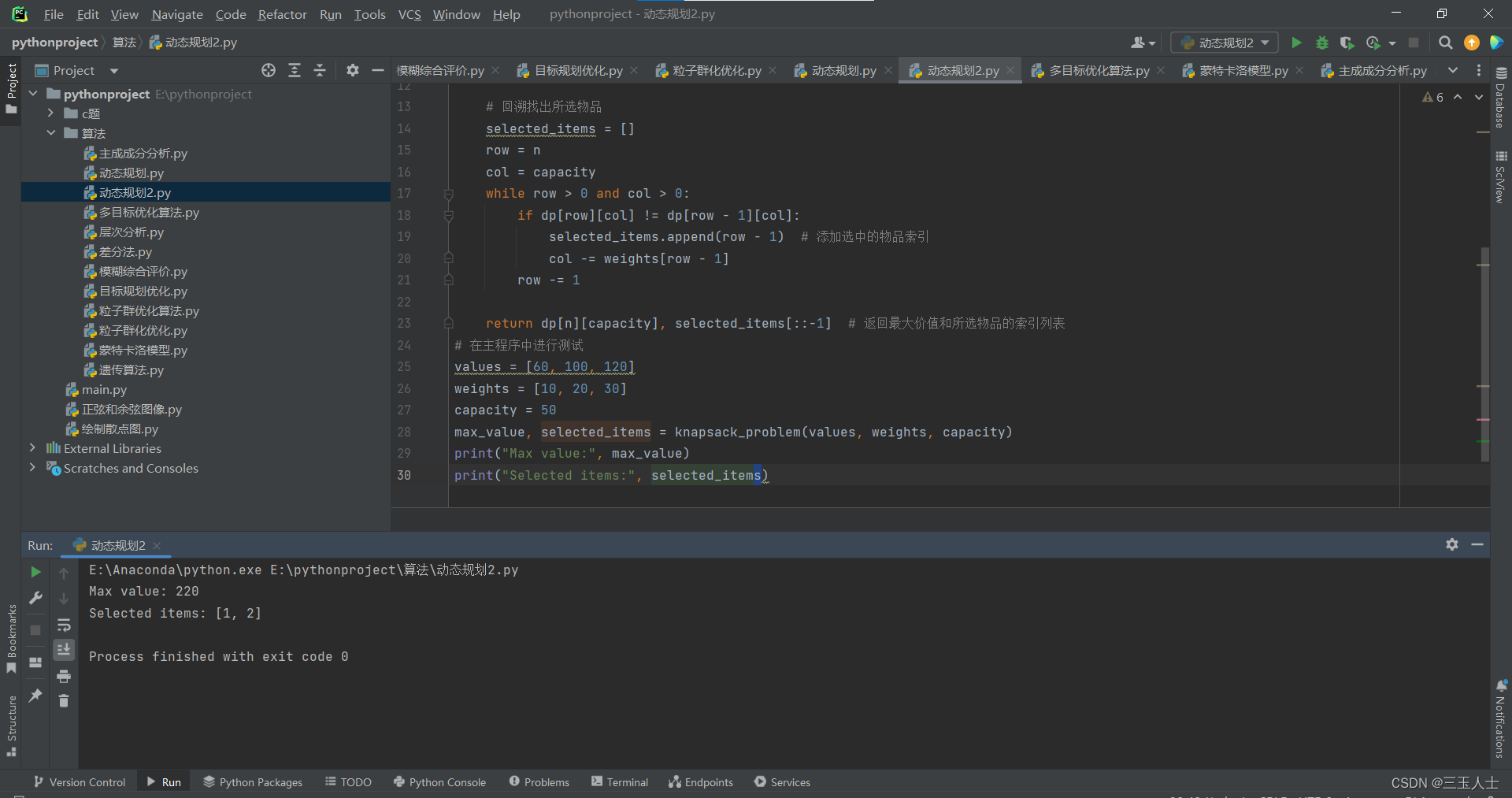
def knapsack_problem(values, weights, capacity):n = len(values) # 物品数量dp = [[0] * (capacity + 1) for _ in range(n + 1)] # 初始化二维表格for i in range(1, n + 1):for j in range(1, capacity + 1):if weights[i - 1] <= j:dp[i][j] = max(dp[i - 1][j], values[i - 1] + dp[i - 1][j - weights[i - 1]])else:dp[i][j] = dp[i - 1][j]# 回溯找出所选物品selected_items = []row = ncol = capacitywhile row > 0 and col > 0:if dp[row][col] != dp[row - 1][col]:selected_items.append(row - 1) # 添加选中的物品索引col -= weights[row - 1]row -= 1return dp[n][capacity], selected_items[::-1] # 返回最大价值和所选物品的索引列表
# 在主程序中进行测试
values = [60, 100, 120]
weights = [10, 20, 30]
capacity = 50
max_value, selected_items = knapsack_problem(values, weights, capacity)
print("Max value:", max_value)
print("Selected items:", selected_items)上述代码解决了经典的背包问题,目标是在给定背包容量下,选择物品使得总价值最大化。其中 values 和 weights 分别表示物品的价值和重量, capacity 表示背包的容量。代码使用动态规划的方法,通过填充二维表格 dp 来求解最大总价值。 最终,代码返回背包能够装下的最大价值 max_value 以及所选物品的索引列表 selected_items 。 需要注意的是,在实际应用中,不同的背包问题可能会有一些变种,例如带有物品数量限制、限制选择物品的次数等。在解决具体问题时,需要根据问题的要求进行适当的变动和调整。
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】 进行投诉反馈!