【多式联运】基于帝企鹅AFO 粒子群PSO 遗传GA算法求解不确定多式联运路径优化问题附matlab代码
✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
⛄ 内容介绍
随着"一带一路"国家战略的推进和建设,中新物流通道在衔接"丝绸之路经济带"和"海上丝绸之路"中的作用日益明显.集装箱多式联运是中新贸易的主要实现形式,目前,多式联运路径优化问题是多式联运相关研究领域的热点.然而多式联运路径优化过程即不同参与者的权衡过程,由于不同商品的特性差异,运输活动中不同参与者对集装箱多式联运的要求也不尽相同.随着"绿色物流"逐渐深入人们的生活,运输过程中的碳排放也受到政府部门越来越多的关注.
⛄ 部分代码
clc;
clear all;
close all;
warning off
%%
noRng=1;
rng('default')
rng(noRng)
%%
global data
data.numN=15; %节点数量
data.Cap_Ts=xlsread("节点处的最大中转运输能力.xlsx");
temp=round(rand(data.numN,3)*10+15)*10;
data.Cap_Ts(:,2:end)=temp;
data.Windows=xlsread("节点的时间窗.xlsx");
data.D=xlsread("节点间距离.xlsx");
data.Cap_Tp=xlsread("节点间最大运输能力.xlsx");
data.T=data.D;
data.v=[76,60,30];
for i=1:length(data.Cap_Tp(:,1))
no1=data.Cap_Tp(i,1);
no2=data.Cap_Tp(i,2);
for j=1:3
if isnan(data.Cap_Tp(i,2+j))
data.D(i,2+j)=nan;
end
end
data.T(i,[3,6,9])=round(data.D(i,3:5)./data.v/1.2);
data.T(i,[4,7,10])=round(data.D(i,3:5)./data.v);
data.T(i,[5,8,11])=round(data.D(i,3:5)./data.v/0.8);
end
data.Windows(:,3)=data.Windows(:,3).*(1-rand(size(data.Windows(:,3))));
data.Windows(:,4)=data.Windows(:,4).*(1+rand(size(data.Windows(:,3))))+10;
data.Windows(:,3:4)=max(0,round(data.Windows(:,3:4)+randn(size(data.Windows(:,3:4)))));
data.Windows(:,5)=max(data.Windows(:,4));
data.CT=[0,3.09,5.23; % 转换成本
3.09,0,26.62;
5.23,26.62,0];
data.TT=[0,1,1; %转换时间
1,0,2;
1,2,0];
data.ET=[0,1.56,6; % 转换碳排放
1.56,0,3.12;
6,3.12,0];
data.q=[120,150,180];
data.E0=[0.796,0.028,0.04];
data.CW=[30,50];
data.S=1;
data.E=15;
data.alpha=0.8;
data.beta1=0.8;
data.beta2=0.8;
data.beta3=0.8;
data.C0=[0.3,0.2,0.1]; %三种运输方式的运输成本
data.weight=[1,1];
data.maxB=100000;
data.maxE=21000;
%%
%%
data.numQ=100;
for i=1:data.numQ
if rand<0.5
data.q0(i)=rand*(data.q(2)-data.q(1))+data.q(1);
else
data.q0(i)=rand*(data.q(3)-data.q(2))+data.q(2);
end
end
%%
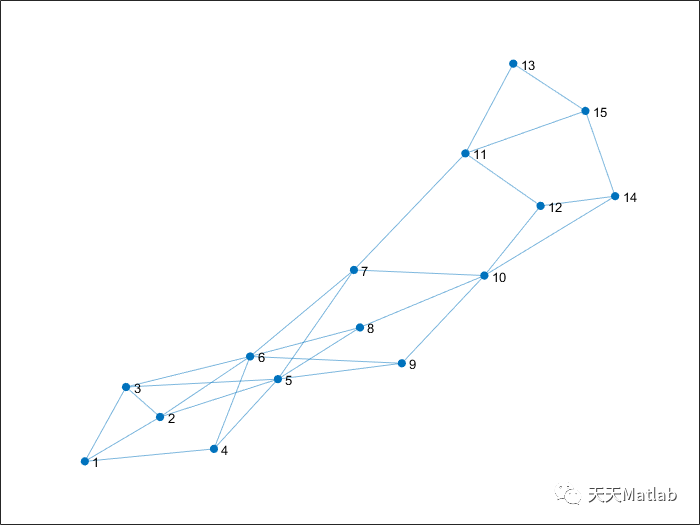
G=graph(data.D(:,1),data.D(:,2),data.D(:,1)*0+1);
figure
plot(G)
set(gca,'LooseInset',get(gca,'TightInset'))
%%
lb=0;
ub=1;
dim=length(data.D(:,1))*3;
option.lb=lb;
option.ub=ub;
option.dim=dim;
if length(option.lb)==1
option.lb=ones(1,option.dim)*option.lb;
option.ub=ones(1,option.dim)*option.ub;
end
option.fobj=@aimFcn_1;
option.showIter=0;
%% 算法参数设置 Parameters
% 基本参数
option.numAgent=20; %种群个体数 size of population
option.maxIteration=100; %最大迭代次数 maximum number of interation
%% 遗传算法
option.p1_GA=0.7;
option.p2_GA=0.1;
%% 粒子群
option.w_pso=0.1;
option.c1_pso=1.2;
option.c2_pso=1.2;
%% AFO
option.v_lb=-(option.ub-option.lb)/4;
option.v_ub=(option.ub-option.lb)/4;
option.w2=0.5; %weight of Moving strategy III
option.w4=1;%weight of Moving strategy III
option.w5=1;%weight of Moving strategy III
option.pe=0.01; % rate to judge Premature convergence
option.gap0=ceil(sqrt(option.maxIteration*2))+1;
option.gapMin=5; % min gap
option.dec=2; % dec of gap
option.L=10; % Catastrophe
%% DE
option.F=0.5;
option.CR=0.5;
%%
str_legend=[{'GA'},{'PSO'},{'AFO'}];
aimFcn=[{@GA},{@PSO},{@AFO3}];
%% 初始化
rng(noRng)
x=ones(option.numAgent,option.dim);
y=ones(option.numAgent,1);
for i=1:option.numAgent
x(i,:)=rand(size(option.lb)).*(option.ub-option.lb)+option.lb;
y(i)=option.fobj(x(i,:),option,data);
end
%% 使用算法求解
bestX=x;
for i=1:length(aimFcn)
rng(noRng)
tic
[bestY(i,:),bestX(i,:),recording(i)]=aimFcn{i}(x,y,option,data);
tt(i)=toc;
end
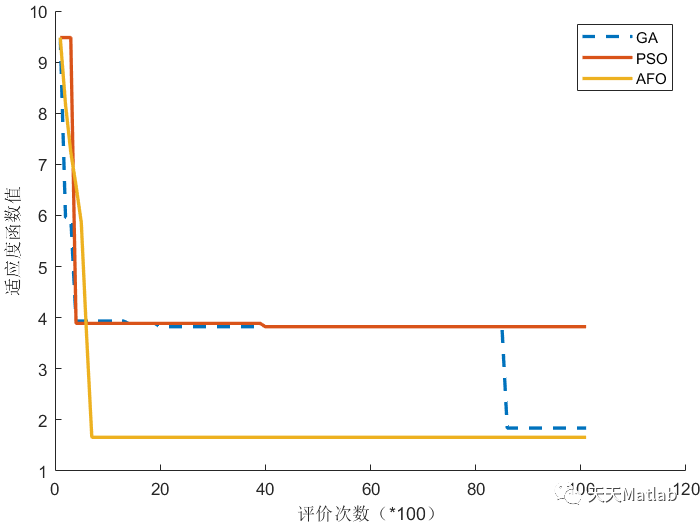
%% 绘制迭代曲线
figure
hold on
for i=1:length(aimFcn)
if i>1
plot((recording(i).bestFit),'LineWidth',2)
else
plot((recording(i).bestFit),'--','LineWidth',2)
end
end
legend(str_legend)
xlabel('评价次数(*100)')
ylabel('适应度函数值')
set(gca,'LooseInset',get(gca,'TightInset'))
%% 计算结果
for i=1:length(str_legend)
str=[str_legend{i},'优化后方案'];
[~,result(i)]=option.fobj(bestX(i,:),option,data);
% drawPC(result(i),data,str)
end
%%
rng(11)
x0=[0.227391667368465 0.879816756512174 0.758978072405287 0.510838515791228 0.192188536212261 0.651441269146713 0.418963422194475 0.552435663022093 0.692178644766480 0.525121273337296 0.901443303774014 0.870433999021102 0.727907836575027 0.635555150728710 0.377948489141470 0.0665747380900594 0.380375322185706 0.271295139005737 0.556390072117235 0.836324594294146 0.412650509862244 0.435408044462144 0.339160221282954 0.517673083186858 0.305139543163461 0.759153928221489 0.661651047625365 0.695663261206050 0.579862243307374 0.0203768757943083 0.567587976562174 0.417560315118765 0.194865572678659 0.0355023446924871 0.0656090882042756 0.283822647397696 0.409304642722500 0.797371466667136 0.139734109717042 0.943567670211017 0.736340144724420 0.899302180486718 0.0958418793238567 0.494947220485218 0.377043083335839 0.392090901825893 0.872224588221799 0.225018973369553 0.658496649609525 0.985772242893824 0.312242936944674 0.0176752228038184 0.151305501546866 0.117920480497746 0.137344184189911 0.929080746036836 0.737056036783124 0.264583371593473 0.935709972806256 0.930542122124921 0.458371373498295 0.0216966409045397 0.0615124906604629 0.569072523079761 0.912715979600965 0.684016483416011 0.0872976004423956 0.854123989826840 0.699891878132857 0.603233918882651 0.626266466189881 0.764357628595205 0.633979476955922 0.162893341780099 0.277411062836412 0.839224723775726 0.908550538167801 0.890586782754062 0.466391769502905 0.488448750263230 0.365236675941588 0.730292329677324 0.748971571306197 0.706903738180738];
gs = GlobalSearch;
problem = createOptimProblem('fmincon','x0',x0,...
'objective',@(x)aimFcn_1(x,option,data),'lb',x0*0,'ub',x0*0+1);
x = run(gs,problem);
[fit1,result(i+1)]=aimFcn_1(x,option,data);
%%
P=[
1 1 1 1 0.610000000000000
0.610000000000000 1 1 0.810000000000000 0 0
0.830000000000000 0.920000000000000 1 1 0.900000000000000 0.830000000000000
1 1 1 0.930000000000000 1 0.930000000000000]; %注 P是从result里面复制出来的
str_legend=[str_legend,{'GS'}];
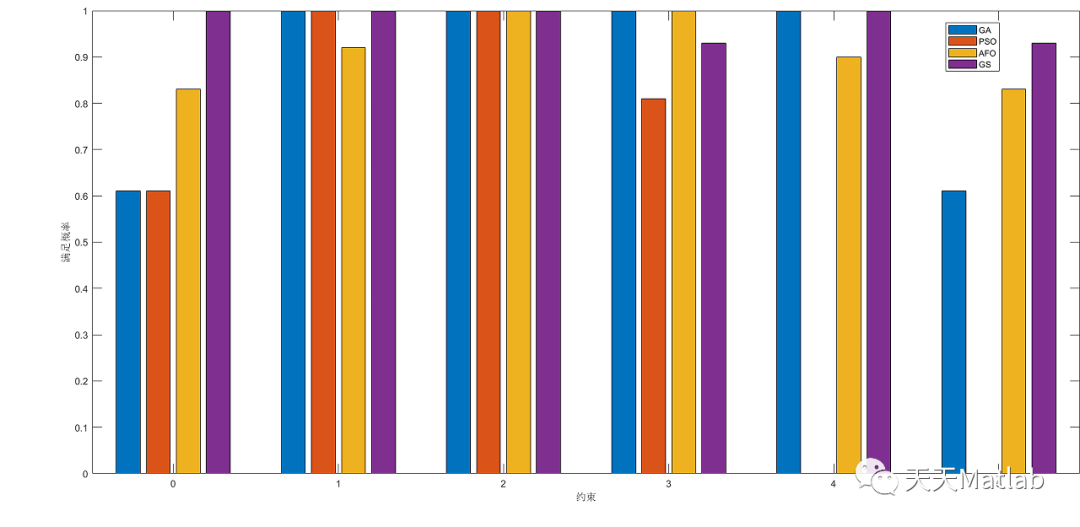
figure
bar(0:5,P,'grouped')
legend(str_legend)
xlabel('约束')
ylabel('满足概率')
set(gca,'LooseInset',get(gca,'TightInset'))
⛄ 运行结果
⛄ 参考文献
[1]何文护. 基于混合遗传算法的多式联运优化的选择研究[D]. 大连海事大学, 2011.
[2]李干亮. 基于多维视角的中新集装箱多式联运路径优化研究[D]. 重庆交通大学, 2019.
⛄ 完整代码
❤️部分理论引用网络文献,若有侵权联系博主删除
❤️ 关注我领取海量matlab电子书和数学建模资料
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!