算法设计与分析复习01：主方法求递归算法时间复杂度

作者：非妃是公主
专栏：《算法》
个性签：顺境不惰，逆境不馁，以心制境，万事可成。——曾国藩

专栏系列文章

算法设计与分析复习01：主方法求递归算法时间复杂度

算法设计与分析复习02：分而治之算法

算法设计与分析复习03：动态规划算法
算法设计与分析复习04：贪心算法

算法设计与分析复习05：回溯及分支限界

算法设计与分析复习06：随机化算法

算法设计与分析复习07：样题

文章目录

• • 专栏系列文章
  • 复习重点
  • 算法复杂度分析——主方法
  • • 例题1：
    • 例题2：
    • 例题3：

复习重点

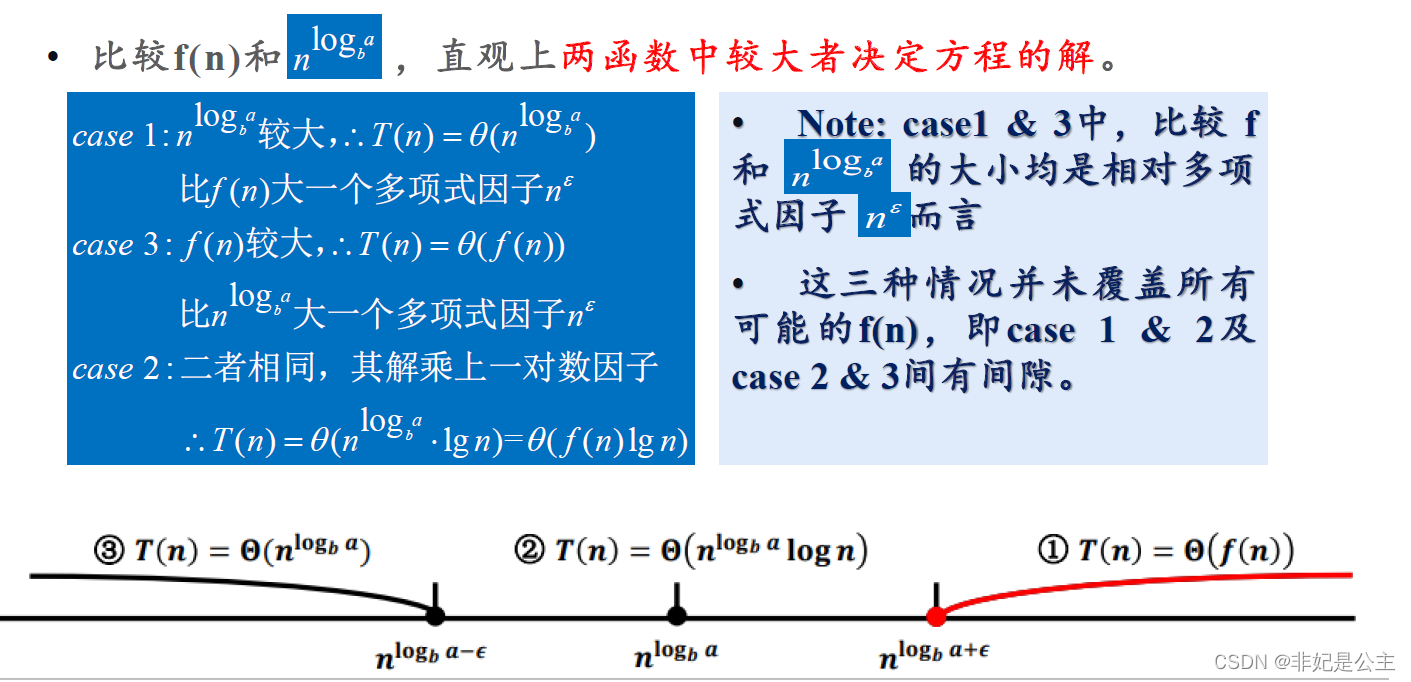
算法复杂度分析——主方法

T ( n ) = a T ( n b ) + f ( n ) T(n)=aT(\frac{n}{b})+f(n) T(n)=aT(bn​)+f(n)

• 其中 a≥1 和 b>1 是常数， f(n) 是渐进函数 。
• 上述递归式描述的是这样一种算法的运行时间：
  • 它将规模为 n 的问题分解为 a 个子问题 每个子问题规模为 n b \frac{n}{b} bn​ ，其中 a 和 b 都是正常数。
  • a 个子问题递归地进行求解，每个花费时间 T(n/b) 。
  • 函数 f(n) 包含了问题分解和子问题解合并的代价 。
  • 其中 n b \frac{n}{b} bn​ 指 n b \frac{n}{b} bn​ 的上取整或者是下取整，对结果不会造成影响。

例题1：

例题2：

例题3：

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！