文章目录

• 一、简介
• • 1.1 KDL库简介
  • 1.2 LM算法原理简介
• 二、源码解析

一、简介

1.1 KDL库简介

KDL库GitHub地址：https://github.com/orocos/orocos_kinematics_dynamics
KDL库包括了运动学、动力学、轨迹插值等功能。
KDL库运动学逆解共有三种算法，都是数值解法：
1、class ChainIkSolverPos_NR——Netwon Rapson迭代法;
2、class ChainIkSolverPos_NR_JL ——Netwon Rapson迭代法（关节限制）;
3、class ChainIkSolverPos_LMA ——LM（Levenberg Marquartdt）迭代算法;
基于LM算法的逆解稳定性相对稍微好一点。

这里有KDL库的一些解析。

1.2 LM算法原理简介

其中，通过sigma的奇异值进行平方运算加上lambda的公式为：

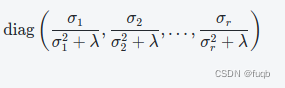
参考文献：
[1].Introduction to Inverse Kinematics with Jacobian Transpose, Pseudoinverse and Damped Least Squares methods. Samuel R. Buss.University of California. 2019.
[2] METHODS FOR NON-LINEAR LEAST SQUARES PROBLEMS.

二、源码解析

int ChainIkSolverPos_LMA::CartToJnt(const KDL::JntArray& q_init, const KDL::Frame& T_base_goal, KDL::JntArray& q_out) {if (nj != chain.getNrOfJoints())return (error = E_NOT_UP_TO_DATE);if (nj != q_init.rows() || nj != q_out.rows())return (error = E_SIZE_MISMATCH);using namespace KDL;double v      = 2;//步长double tau    = 10;double rho;double lambda;//拉格朗日乘子Twist t;double delta_pos_norm;Eigen::Matrix<ScalarType,6,1> delta_pos;//位置姿态误差Eigen::Matrix<ScalarType,6,1> delta_pos_new;q=q_init.data.cast<ScalarType>();compute_fwdpos(q);//计算运动学正解，得到T_base_head，即当前角度q条件下，机械臂末端head//相对于base的变换矩阵Twist_to_Eigen( diff( T_base_head, T_base_goal), delta_pos );//计算当前误差，得到//delta_pos，6*1的vertor，前3个元素为位置误差，欧式距离，后三个元素为角度误差，使用的是//轴角表示，即轴（3*1）乘以角度，以上误差均在base坐标系下表示，对应图1第2步.delta_pos=L.asDiagonal()*delta_pos;delta_pos_norm = delta_pos.norm();if (delta_pos_norm<eps) {//如果步长太小，则认为已经达到目标处，迭代结束.lastNrOfIter    =0 ;Twist_to_Eigen( diff( T_base_head, T_base_goal), delta_pos );lastDifference  = delta_pos.norm();lastTransDiff   = delta_pos.topRows(3).norm();lastRotDiff     = delta_pos.bottomRows(3).norm();svd.compute(jac);original_Aii    = svd.singularValues();lastSV          = svd.singularValues();q_out.data      = q.cast<double>();return (error = E_NOERROR);}compute_jacobian(q);//计算space雅克比矩阵，图1第3步.jac = L.asDiagonal()*jac;//雅克比加权lambda = tau;double dnorm = 1;for (unsigned int i=0;i<maxiter;++i) {svd.compute(jac);//**********Segment A start******************//original_Aii = svd.singularValues()for (unsigned int j=0;j<original_Aii.rows();++j) {original_Aii(j) = original_Aii(j)/( original_Aii(j)*original_Aii(j)+lambda);//原理看图1.3}tmp = svd.matrixU().transpose()*delta_pos;tmp = original_Aii.cwiseProduct(tmp);diffq = svd.matrixV()*tmp;//**********Segment A end****************////Segment A 段数学原理看图1.2与图1.3grad = jac.transpose()*delta_pos;if (display_information) {std::cout << "------- iteration " << i << " ----------------\n"<< "  q              = " << q.transpose() << "\n"<< "  weighted jac   = \n" << jac << "\n"<< "  lambda         = " << lambda << "\n"<< "  eigenvalues    = " << svd.singularValues().transpose() << "\n"<< "  difference     = "   << delta_pos.transpose() << "\n"<< "  difference norm= "   << delta_pos_norm << "\n"<< "  proj. on grad. = "   << grad << "\n";std::cout << std::endl;}dnorm = diffq.lpNorm<Eigen::Infinity>();if (dnorm < eps_joints) {lastDifference = delta_pos_norm;lastNrOfIter   = i;lastSV         = svd.singularValues();q_out.data     = q.cast<double>();compute_fwdpos(q);Twist_to_Eigen( diff( T_base_head, T_base_goal), delta_pos );lastTransDiff  = delta_pos.topRows(3).norm();lastRotDiff    = delta_pos.bottomRows(3).norm();return (error = E_INCREMENT_JOINTS_TOO_SMALL);}if (grad.transpose()*grad < eps_joints*eps_joints ) {compute_fwdpos(q);Twist_to_Eigen( diff( T_base_head, T_base_goal), delta_pos );lastDifference = delta_pos_norm;lastTransDiff = delta_pos.topRows(3).norm();lastRotDiff   = delta_pos.bottomRows(3).norm();lastSV        = svd.singularValues();lastNrOfIter  = i;q_out.data    = q.cast<double>();return (error = E_GRADIENT_JOINTS_TOO_SMALL);}q_new = q+diffq;//图1第5步compute_fwdpos(q_new);Twist_to_Eigen( diff( T_base_head, T_base_goal), delta_pos_new );delta_pos_new             = L.asDiagonal()*delta_pos_new;double delta_pos_new_norm = delta_pos_new.norm();rho                       = delta_pos_norm*delta_pos_norm - delta_pos_new_norm*delta_pos_new_norm;rho                      /= diffq.transpose()*(lambda*diffq + grad);if (rho > 0) {q               = q_new;delta_pos       = delta_pos_new;delta_pos_norm  = delta_pos_new_norm;//更新参数，图1第6步if (delta_pos_norm<eps) {Twist_to_Eigen( diff( T_base_head, T_base_goal), delta_pos );lastDifference = delta_pos_norm;lastTransDiff  = delta_pos.topRows(3).norm();lastRotDiff    = delta_pos.bottomRows(3).norm();lastSV         = svd.singularValues();lastNrOfIter   = i;q_out.data     = q.cast<double>();return (error = E_NOERROR);}compute_jacobian(q_new);jac = L.asDiagonal()*jac;double tmp=2*rho-1;lambda = lambda*max(1/3.0, 1-tmp*tmp*tmp);v = 2;} else {lambda = lambda*v;//图1第7步更新v      = 2*v;}}lastDifference = delta_pos_norm;lastTransDiff  = delta_pos.topRows(3).norm();lastRotDiff    = delta_pos.bottomRows(3).norm();lastSV         = svd.singularValues();lastNrOfIter   = maxiter;q_out.data     = q.cast<double>();return (error = E_MAX_ITERATIONS_EXCEEDED);}

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！