基于Python——Kmeans聚类算法的实现

1、概述

本篇博文为数据挖掘算法系列的第一篇。现在对于Kmeans算法进行简单的介绍，Kmeans算法是属于无监督的学习的算法，并且是最基本、最简单的一种基于距离的聚类算法。

下面简单说一下Kmeans算法的步骤：

1. 选随机选取K的簇中心（注意这个K是自己选择的）
2. 计算每个数据点离这K个簇中心的距离，然后将这个点划分到距离最小的簇中
3. 重新计算簇中心，即将每个簇的所有数据点相加求均值，将这个均值作为对应簇的新簇中心。
4. 重复2、3步，直到满足了你设置的停止算法迭代的条件

注意：停止算法迭代的条件一般有三个：

1. 没有（或最小数目）对象被重新分配给不同的聚类。
2. 没有（或最小数目）聚类中心再发生变化。
3. 误差平方和局部最小。

常用的距离公式有：1、欧式距离； 2、曼哈顿距离；3、切比雪夫距离等等

二、实现

下面给出实现代码，在这里我设置的停止条件是第三种，即误差平方和最小

import numpy as np
import random
import matplotlib.pyplot as plt
from calculate_distance_algorithm import euclid_distanceplt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号class KMeans:def __init__(self, n_cluster, algorithm=euclid_distance, iterators=None):self.n_cluster = n_clusterself.cluster_centers_ = Noneself.algorithm = euclid_distanceself.iterations = iteratorsself.loss = Nonedef fit(self, data):"""进行k-means算法迭代，划分簇:param Y: Y是对应X正确的种类:param iterators: 算法迭代次数:param data: 数据集(X, Y) X是测试点，:param k:最终要划分出簇的个数:param calculate_method:计算距离使用的公式 默认为计算两点间的欧式距离，可以通过传递计算距离的方法名来更改计算距离方式"""# 获得随机划分的质心clusters = self.random_choose_cluster(data, self.n_cluster)clusters_collection = {}# 一开始的损失值loss_value = 1 << 30# 统计迭代次数count = 0while True:# 如果达到了指定的迭代次数后，就不迭代了if count == self.iterations and self.iterations != -1:breakcount += 1# 初始化每个簇集合for index, cluster in enumerate(clusters):clusters_collection[index] = []for pos, x in enumerate(data):min = 1 << 30min_index = -1# 遍历每个数据，计算与k个簇的质心的距离for index, cluster in enumerate(clusters):# 计算每个点与对应质心的距离dis = self.algorithm(x, cluster)if dis < min:min = dismin_index = index# 将这个数据点划分到距离最近的簇中clusters_collection[min_index].append(x)# 计算当前的损失值now_loss_value = self.loss_function(clusters_collection, clusters)if now_loss_value > loss_value:# 重新计算每个簇的质心self.calculate_centroid(clusters_collection, clusters)elif now_loss_value < loss_value:print("算法正在运行，迭代次数:{}".format(count))# 重新计算每个簇的质心self.calculate_centroid(clusters_collection, clusters)elif now_loss_value == loss_value:self.cluster_centers_ = clustersself.loss = now_loss_valuereturn self# 更新损失值loss_value = now_loss_valuedef predict(self, X):"""预测函数:param X: 需要预测的数据点:param clusters: 分配好了的簇中心集合:return: 返回对应数据点预测对应的簇种类"""result = []for x in X:min_index = -1max_dis = 1 << 30for index, i in enumerate(self.cluster_centers_):dis = self.algorithm(x, i)if max_dis > dis:max_dis = dismin_index = indexresult.append(min_index)return np.array(result)def random_choose_cluster(self, data, k):"""随机在数据data中选取k个簇:param data: 数据集:param k: 选取的簇的个数:return: 返回包含选取k个簇坐标的列表"""clusters = []pos = random.sample(range(len(data)), k)for i in pos:clusters.append(data[i])return np.array(clusters)def calculate_centroid(self, collection, clusters):"""计算集合的质心计算方法：将对应集合所有数据的x、y加起来，求平均值，将这个平均值点返回:param collection: 需要计算质心的集合:return: 返回这个集合的质心"""# 重新计算每个簇的质心for i in collection.keys():if len(collection[i]) > 0:result = np.mean(collection[i], axis=0)clusters[i] = resultdef loss_function(self, data, clusters):"""衡量K-means算法停止迭代的损失函数:param data: 所有簇集合:param clusters: 每个簇对应的质心:return: 返回损失值"""total = 0for i in data:for x in data[i]:total += self.algorithm(x, clusters[i])return total

距离算法公式实现(calculate_distance_algorithm.py)：

import numpy as np
def manhattan_distance(x1, x2):"""计算两点间的曼哈顿距离:param x1:(x1, y1):param x2:(x2, y2):return:返回两点之间的曼哈顿距离"""result = np.abs(x1[0] - x2[0]) + np.abs(x1[1] - x1[1])return resultdef chebyshev_distance(x1, x2):"""计算两点间的切比雪夫距离:param x1:(x1, y1):param x2:(x2, y2):return:返回两点之间的切比雪夫距离"""return np.max(np.abs(x1 - x2))def euclid_distance(x1, x2):"""计算两点间的欧式距离:param x1:(x1, y1):param x2:(x2, y2):return: 返回两点之间的欧式距离"""return np.sqrt(np.sum((x1 - x2) ** 2))

下面给出使用Kmeans聚类算法对图片进行聚类的实现。

聚类图片对象为：

聚类结果图像：

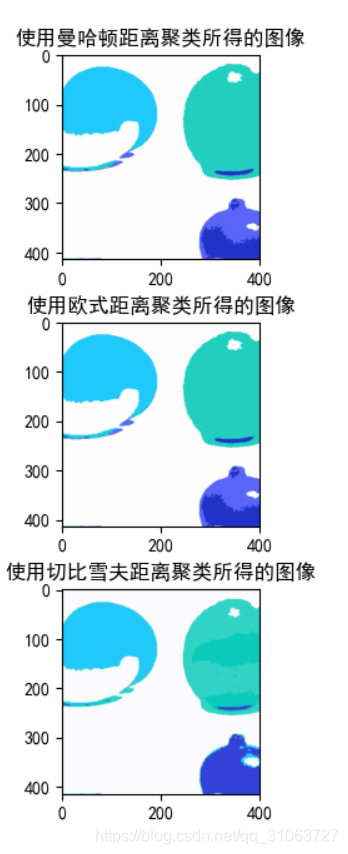
测试代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
import cv2 as cv
from K_means import KMeans
from calculate_distance_algorithm import manhattan_distance, chebyshev_distance, euclid_distancedef recreate_image(clusters, labels, w, h):"""重新创建图像:param clusters: 聚类中心:param labels: 预测的种类集合:param w: 图像的宽:param h: 图像的高:return: 返回图像"""d = clusters.shape[1]# 构建图像 w：宽， h:高， d:聚类个数# print(clusters)image = np.zeros((w, h, d))label_idx = 0for i in range(w):for j in range(h):image[i][j] = clusters[labels[label_idx]]# print(image[i][j])label_idx += 1return imagedef get_data(data, k):"""将对应的三维数组转换成 n*4维的矩阵，前3列是数据，最后一列是该类数据对应的样本标签值k:param data: 数据:param k: 标签:return: 转换好的n*4维数据"""# 展开成n*3维data = data.reshape(-1, 3)# 生成颜色对应的标签data_label = np.ones((data.shape[0], 1))data_label *= k# 将标签列与数据合并return np.hstack((data, data_label))if __name__ == '__main__':# ----------------------------->读入数据，创建数据集并划分训练集和测试集<-----------------------------#file = "fruit.jpg"img = cv.imread(file)img[img == 0] = 1  # 将0值填充为1，防止后续聚类出现nan值img = np.array(img, dtype=np.float32) / 255  # 除255进行归一化，变成(0, 1)# 选取黑色部分的数据black = img[239:243, 320:360]black = get_data(black, 0)# 选取白色部分的数据white = img[280:360, 30:110]white = get_data(white, 1)# 选取黄色部分的数据yellow = img[60:130, 30:110]yellow = get_data(yellow, 2)# 选取绿色部分的数据green = img[70:210, 290:370]green = get_data(green, 3)# 选择红色数据red = img[340:410, 310:390]red = get_data(red, 4)# 总数据data = np.vstack((black, white, yellow, green, red))# 划分测试集和训练集x_train, x_test, y_train, y_test = train_test_split(data[:, :3], data[:, -1],test_size=0.3, random_state=0, shuffle=True)# 转换成numpy的array形式x_train = np.array(x_train)x_test = np.array(x_test)y_train = np.array(y_train)y_test = np.array(y_test)# -------------------------------------->对图片进行聚类<--------------------------------------## 获得图片的宽、高、颜色深度w, h, d = img.shape# 展开成n*3维的矩阵，-1代表自适应img = np.array(img.reshape(-1, 3), dtype=np.float64)# -----------------------------使用曼哈顿距离进行聚类-----------------------------plt.figure()plt.subplot(3, 1, 1)print("使用曼哈顿距离聚类开始。。。。。。。")# 建立Kmeans分类estimator = KMeans(n_cluster=5, algorithm=manhattan_distance)  # 默认是使用欧式距离计算# 使用训练集来聚类，找到每个种类对应的簇中心estimator.fit(x_train)# 根据训练好的结果，对整个图像进行聚类y_predict = estimator.predict(img)# 将聚类结果显示image = recreate_image(estimator.cluster_centers_, y_predict, w, h)plt.title("使用曼哈顿距离聚类所得的图像")plt.imshow(image)# -----------------------------使用欧式距离进行聚类-----------------------------# 建立Kmeans分类plt.subplot(3, 1, 2)print("使用欧式距离聚类开始。。。。。。。")estimator = KMeans(n_cluster=5, algorithm=euclid_distance)  # 默认是使用欧式距离计算# 使用训练集来聚类，找到每个种类对应的簇中心estimator.fit(x_train)# 根据训练好的结果，对整个图像进行聚类y_predict = estimator.predict(img)# 将聚类结果显示image = recreate_image(estimator.cluster_centers_, y_predict, w, h)plt.title("使用欧式距离聚类所得的图像")plt.imshow(image)# -----------------------------使用切比雪夫距离进行聚类-----------------------------# 建立Kmeans分类plt.subplot(3, 1, 3)print("使用切比雪夫距离聚类开始。。。。。。。")estimator = KMeans(n_cluster=5, algorithm=chebyshev_distance)  # 默认是使用欧式距离计算# 使用训练集来聚类，找到每个种类对应的簇中心estimator.fit(x_train)# 根据训练好的结果，对整个图像进行聚类y_predict = estimator.predict(img)# 将聚类结果显示image = recreate_image(estimator.cluster_centers_, y_predict, w, h)plt.title("使用切比雪夫距离聚类所得的图像")plt.imshow(image)plt.show()

因为聚类是无监督的学习算法，所以一般来说是不会用来分类的。评价一个聚类模型的好坏，可以根据模型的轮廓系数来判定，至于这个轮廓系数是啥东西，大家可以参考sklearn关于Kmeans的说明，或者百度，Google。

本文来自互联网用户投稿，文章观点仅代表作者本人，不代表本站立场，不承担相关法律责任。如若转载，请注明出处。 如若内容造成侵权/违法违规/事实不符，请点击【内容举报】进行投诉反馈！