一维信号光滑去毛刺处理
以下是威斯康星大学交通系博士申请遇到的一道题,有兴趣的可以交流
Problem:
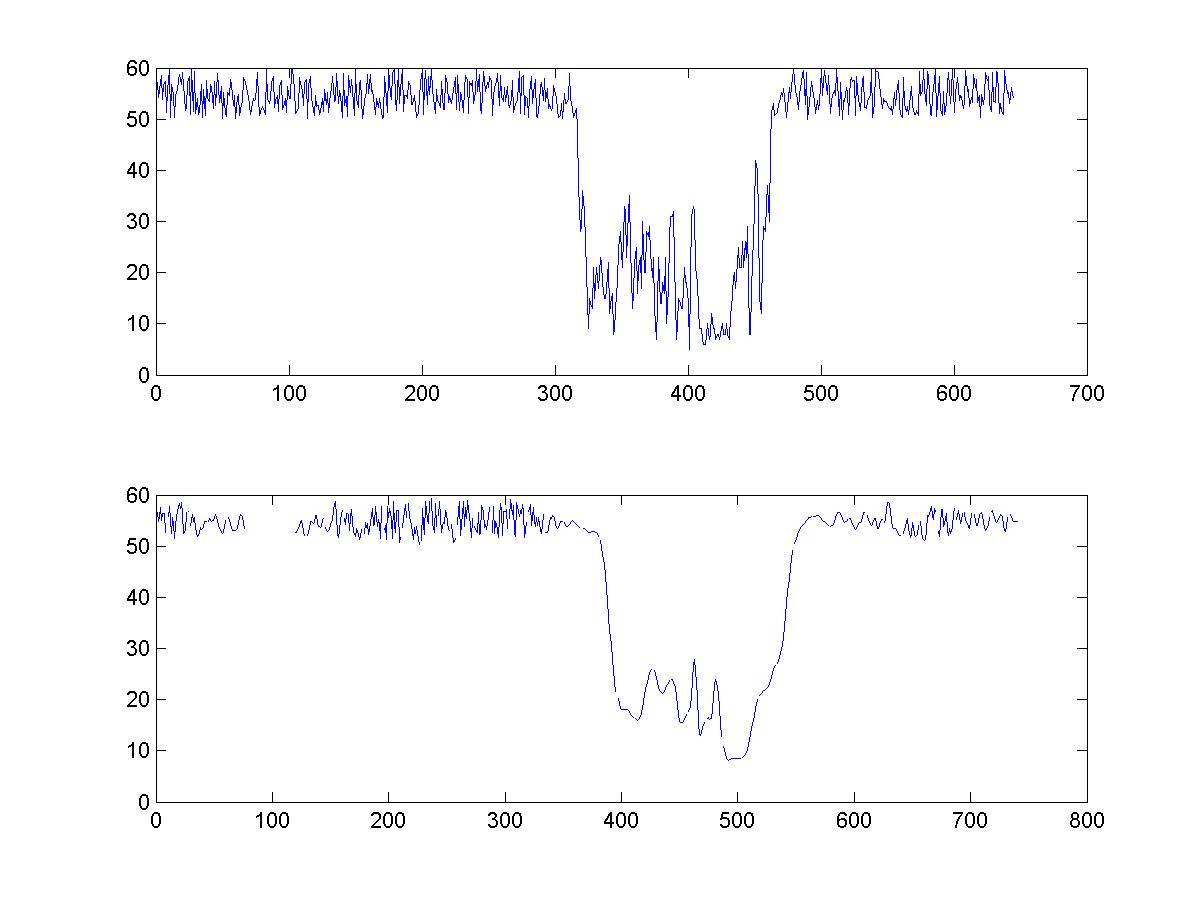
Implement theKalman Filter (Use identity matrix for statepropagation)or other smoothing filter of your choice on the enclosed “speed24.csv” .Compare the filtered and the original data in a time-series plot (x: timeinterval, y: speed data). Report ME, MAE, and MAPE of the filtering results. Ifthe filter contains any parameters, e.g.smoothing window,smoothing coefficient, experiment to find the best fittingparameters that produces the best trend of the original data.( 平滑窗口,平滑参数,试验找到最好的拟合参数以得到原始数据的最好趋势。)
以下是matlab实现的算法
[plain] view plain copy
- function xdense = linear_interp(x, t, tdense)
- xdense = zeros(size(tdense));
- for i = 1:length(tdense)
- ind_b = find(tdense(i) >= t, 1, 'last');
- if isempty(ind_b)
- ind_b = 1;
- ind_e = 1;
- lambda = 1;
- elseif ind_b == length(t)
- ind_e = ind_b;
- lambda = 0;
- else
- ind_e = ind_b + 1;
- lambda = (tdense(i) - t(ind_b)) / (t(ind_e) - t(ind_b));
- end;
- xdense(i) = (1 - lambda) * x(ind_b) + lambda * x(ind_e);
- end;
[plain] view plain copy
- %--------------------------------------------------------------------------
- % apply fourier analysis on each window size, estimate the dominant
- % frequency, and remove high freqs...
- % partition the signals and perform fourier analysis so that we get the
- % dominant freq, then smooth the signal using sigma that changes with the
- % dominant freq...
- %--------------------------------------------------------------------------
- clear all;
- %clc;
- %close all;
- % 可以调整的参数
- windowSize = 41;
- % step 1: read signals from input file
- FILE_PATH = 'E:\data.csv';
- signal = CSVREAD(FILE_PATH);
- S_signal = signal;
- smoothed_result = zeros(length(signal), 1);
- % 不考虑NAN数据
- nan = isnan(signal);
- an = ~isnan(signal);
- signal = signal(~isnan(signal));
- n = length(signal);
- starts = 1:windowSize:n;
- if starts(end) + windowSize > n
- starts(end) = n - windowSize + 1;
- end;
- dominantSigmas_sample = zeros(length(starts), 1);
- % perform fourier analysis.
- for i = 1:length(starts)
- sel = starts(i):starts(i)+windowSize-1;
- coeffs = fft(signal(sel) - mean(signal(sel)));
- % find the dominant one...
- [maxVal, maxIndex] = max(abs(coeffs(1:floor(windowSize/2))));
- dominantSigmas_sample(i) = windowSize / maxIndex/5;
- end;
- % simple local linear interpolate...
- dominantSigmas = linear_interp(dominantSigmas_sample, starts + windowSize/2, (1:n)');
- smoothed_signal = zeros(n, 1);
- % then smooth the signal
- for i = 1:n
- % blur the image locally...
- sigma = dominantSigmas(i);
- % 高斯函数分布特性,
- % http://blog.csdn.net/fullyfulei/article/details/8758372
- span = round(3*sigma);
- sel = (max(1, i - span):min(n, i + span))';
- filter = exp(- (sel - i).^2 / 2 / sigma^2);
- smoothed_signal(i) = sum(signal(sel) .* filter) / sum(filter);
- end
- smoothed_result(nan) = NaN;
- smoothed_result(an) = smoothed_signal;
- maxPoint = [false; smoothed_result(2:end-1) > smoothed_result(3:end) & smoothed_result(2:end-1) > smoothed_result(1:end-2); false];
- minPoint = [false; smoothed_result(2:end-1) < smoothed_result(3:end) & smoothed_result(2:end-1) < smoothed_result(1:end-2); false];
- figure
- subplot(2,1,1)
- plot(S_signal);
- subplot(2,1,2)
- plot(smoothed_result);
- % ME, MAE, MAPE
- E = smoothed_signal - signal;
- AE = abs(E);
- ME = sum(E)/n;
- MAE = sum(AE)/n;
- MAPE = sum(abs(E./signal))/n;
本文来自互联网用户投稿,文章观点仅代表作者本人,不代表本站立场,不承担相关法律责任。如若转载,请注明出处。 如若内容造成侵权/违法违规/事实不符,请点击【内容举报】进行投诉反馈!